零次学习论文介绍
Zero-shot Learning 论文介绍
首发于知乎-SCUT神经网络-Magellan小分队
最近看了一段时间零次学习系列的文章,这里介绍一些代表性的论文,算是对这段时间学习的一个总结,前方公式高能,为了阅读顺畅我会尽量减少一些公式并且尽量解释这些式子,想看完整推导过程的可以自己找原文来看,可能会有理解错误的地方,欢迎指正。
文章目录
- Zero-shot Learning 论文介绍
- 0. 什么是零次学习?
- 1. 对属性进行学习
- 2. 学习从视觉特征空间到语义空间的线性映射
- Label-Embedding for Attribute-Based Classification[^3](2013,CVPR)
- Evaluation of output embeddings for fine-grained image classification(2015,CVPR)
- 3. 非线性映射
- Latent embeddings for zero-shot classification[^7](2016,CVPR)
- 4. 第三方空间
- Zero-shot learning via semantic similarity embedding[^8](2015,ICCV)
- 5. ZSL中存在的问题
- 1)领域漂移问题(domain shift)
- Transductive Multi-View Zero-Shot Learning[^9](2015,TPAMI)
- Semantic Autoencoder for Zero-Shot Learning(2017,CVPR)
- A Generative Adversarial Approach for Zero-Shot Learning from Noisy Texts[^12](2018,CVPR)
- 2) 语义间隔问题(Semantic Gap)
- Zero-Shot Recognition using Dual Visual-Semantic Mapping Paths[^13](2017,CVPR)
- 6. 直推式学习(Transductive Zero-shot Learning)
- Semi-supervised vocabulary-informed learning[^14](2016,CVPR)
- 7. 不使用额外的辅助信息
- Metric learning for large scale image classification: Generalizing to new classes at near-zero cost[^15](2012,ECCV)
- 8. ZSL中的特征提取
- Discriminative Learning of Latent Features for Zero-Shot Recognition[^17](2018,CVPR)
0. 什么是零次学习?
这个问题基本上在每篇零次学习的论文中的引言里都会介绍一遍,这里简单说一下。在零次学习(ZSL)中,训练集中的样本标签与测试集的标签是不相交的,即在训练时是没有见过测试集类别的样本的,而零次学习任务就是要识别出这些训练时没见过的类别的样本。既然要认出没见过的对象,那就要教会模型学习到更“本质”的知识,并且将这些知识“举一反三”,从已见过的类别(seen)迁移到没见过的类别(unseen)。在具体的实现中,模型会使用一层语义嵌入层,作为seen类和unseen类的迁移桥梁或者说中间表示,将seen类的知识迁移到unseen类,教会模型”举一反三“。而这个语义嵌入层具体会是对类别的一些描述,具体可能会是人工定义的属性或者词向量等语义表示。这个问题更生动具体的阐释可以看这篇文章。
接下来我会参考2018年一篇综述1来梳理ZSL的发展脉络。
1. 对属性进行学习
ZSL的开山之作是2009年2的DAP和IAP,引入了类标签的属性层,对每个属性都学习一个二分类器,方法很简单这里不多说,有兴趣可以找来看看。
现在的零次学习方法直接对属性进行学习的其实不多了,因为直接对属性学习会存在几个问题:
- 对属性的进行预测并不是ZSL任务的直接目标,这是间接地解决问题,这样可能会导致一种情况:模型可能对属性的预测是最优的,但对类别的预测未必是最优的。
- 无法利用unseen类的样本提供的先验知识。
- 无法利用属性间的关系等额外的信息,因为每个分类器只是针对一个属性进行学习的。
- 无法利用其他的辅助信息,例如词向量、语义等级层次等其他对类别的描述信息源。
2. 学习从视觉特征空间到语义空间的线性映射
其实很多零次学习的文章都把零次学习任务看作一个从视觉特征空间到语义空间的映射问题,这里首先介绍比较经典的ALE模型,
Label-Embedding for Attribute-Based Classification3(2013,CVPR)
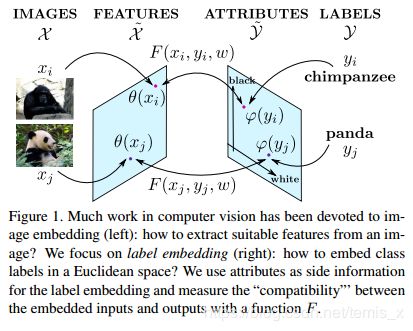
这篇文章就是从以往零次学习对属性学习的缺点出发,提出一个标签嵌入框架,直接解决对类别的预测问题,而不是简单地对属性进行预测。
首先,像其他零次学习方法一样,通过网络提取出图像特征 θ : X → X ~ \theta: \mathcal{X} \rarr \tilde{\mathcal{X}} θ:X→X~,标签 Y \mathcal{Y} Y也嵌入一个属性空间 φ : Y → Y ~ \varphi : \mathcal { Y } \rightarrow \tilde { \mathcal { Y } } φ:Y→Y~。
ALE引入了一个评分函数,来衡量视觉特征空间 x x x嵌入语义空间的兼容度(compatibility),这是一个双线性函数:
(1) F ( x , y ; W ) = θ ( x ) W φ ( y ) F ( x , y ; W ) = \theta ( x ) W \varphi ( y ) \tag 1 F(x,y;W)=θ(x)Wφ(y)(1)
损失函数
设每条训练数据都以 ( x n , y n ) (x_n,y_n) (xn,yn)的形式存在,其中 x n x_n xn 是对象, y n y_n yn是它唯一的一条正确的标签。
ALE的损失函数借鉴了WSABIE和结构化的SVM的损失函数的设置,在损失函数中也使用了hinge loss,(这种设置后面很多方法都有用到,这里会详细介绍一下)但也有所不同:
(2) 1 N ∑ n = 1 N max y ∈ Y ℓ ( x n , y n , y ) \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \max _ { y \in \mathcal { Y } } \ell \left( x _ { n } , y _ { n } , y \right) \tag 2 N1n=1∑Ny∈Ymaxℓ(xn,yn,y)(2)
其中,
(3) ℓ ( x n , y n , y ) = Δ ( y n , y ) + F ( x n , y ; W ) − F ( x n , y n ; W ) \ell \left( x _ { n } , y _ { n } , y \right) = \Delta \left( y _ { n } , y \right) + F \left( x _ { n } , y ; W \right) - F \left( x _ { n } , y _ { n } ; W \right) \tag 3 ℓ(xn,yn,y)=Δ(yn,y)+F(xn,y;W)−F(xn,yn;W)(3)
我们先来分析一些 ℓ \ell ℓ做了什么,它由两部分组成,前面的 Δ \Delta Δ其实是我们常见的分类loss中会出现的,后面这部分其实是基于排序的(ranking-based loss function)。
- 当 y > y n y>y_n y>yn, ℓ = Δ ( y n , y ) + ( F ( x n , y ; W ) − F ( x n , y n ; W ) \ell =\Delta \left( y _ { n } , y \right)+(F(x_n,y;W)-F(x_n,y_n;W) ℓ=Δ(yn,y)+(F(xn,y;W)−F(xn,yn;W), 即排在正确类别前面的类别,即为 Δ ( y n , y ) \Delta \left( y _ { n } , y \right) Δ(yn,y)+两者兼容度的差距,并且排在越前面差距越大,loss越大;
- 当 y n > y , t h e n ℓ = Δ ( y n , y ) − ( F ( x n , y n ; W ) − F ( x n , y ; W ) ) y_n > y, \ then\ \ell=\Delta \left( y _ { n } , y \right)-(\ F(x_n,y_n;W)-F(x_n,y;W)) yn>y, then ℓ=Δ(yn,y)−( F(xn,yn;W)−F(xn,y;W)), 即排在越靠后, ( F y n − F y ) (F_{y_n}-F_y) (Fyn−Fy)越大,loss越小.
在WSABIE4中的loss是考虑了所有类别的,但在ALE中取了max,如等式2,即在所有类别中找出 ℓ \ell ℓ最大的,然后逐样本累加。
最后为了能利用额外的增量信息,ALE还增加了一项,变成:
(4) 1 N ∑ n = 1 N max y ∈ Y ℓ ( x n , y n , y ) + μ 2 ∥ Φ − Φ A ∥ 2 \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \max _ { y \in \mathcal { Y } } \ell \left( x _ { n } , y _ { n } , y \right) + \frac { \mu } { 2 } \left\| \Phi - \Phi ^ { \mathcal { A } } \right\| ^ { 2 } \tag 4 N1n=1∑Ny∈Ymaxℓ(xn,yn,y)+2μ∥∥Φ−ΦA∥∥2(4)
其中 Φ \Phi Φ表示可学习的语义空间, Φ A \Phi^\mathcal{A} ΦA是关于标签的先验知识。
现在我们来回顾一下ALE是否解决了前面的缺点,它们主要体现在loss函数里。首先来看它的loss里的兼容度评判函数是直接与类别相关的,而不是解决中间问题;其次,ALE增加了可学习的语义空间,可以使用额外的增量信息,并且这种可学习的语义空间,很容易引入其他的辅助信息源,例如词向量、等级标签嵌入(HLE)等;最后,ALE直接对类别进行预测,类别会用属性得来的语义向量表示,这样的训练使得属性间是有联系的而不是单独训练预测属性最优。
与ALE较类似的工作还有DeViSE5(学习的是线性映射),而使用其他的语义信息源的工作很多,下面介绍一个具有代表性的SJE6模型。
Evaluation of output embeddings for fine-grained image classification(2015,CVPR)
受前面标签嵌入的方法的启发,本文工作提出了一个结构化的联合嵌入框架(SJE),使用了多种辅助语义信息源,致力于取代ZSL的人工标注属性。
这篇文章的兼容度评判函数以及损失函数的设置其实与ALE大同小异,这里不赘述。这个工作亮点主要体现在联合嵌入,所以它的评判函数组合了多种嵌入:
(5) F ( x , y ; { W } 1 … K ) = ∑ k α k θ ( x ) ⊤ W k φ k ( y ) s.t. ∑ k α k = 1 \begin{array}{c}{F\left(x, y ;\{W\}_{1 \dots K}\right)=\sum_{k} \alpha_{k} \theta(x)^{\top} W_{k} \varphi_{k}(y)} \\ {\text { s.t. } \sum_{k} \alpha_{k}=1}\end{array} \tag 5 F(x,y;{W}1…K)=∑kαkθ(x)⊤Wkφk(y) s.t. ∑kαk=1(5)
并且每个 φ k \varphi_{k} φk都是独立训练的。
这篇文章用到的辅助信息包括了传统的属性、从文本中学习而来的标签嵌入(例如词向量、GloVe、Bag-of-Words等)以及ALE提及的HLE嵌入。
上述提及的ZSL方法,基本上都是使用线性的兼容度评判函数,这是一个全局的线性函数,这对于更复杂的任务来说,例如细粒度任务,表达能力可能有限,自然会有人提出更复杂的非线性模型。
3. 非线性映射
这里介绍一篇基于上面提及的SJE模型的文章,虽然题目没有提及非线性,但其实它是通过一个隐变量,把SJE模型拓展称为一个非线性模型。
Latent embeddings for zero-shot classification7(2016,CVPR)
这篇文章提出的非线性模型(LatEm)其实是一个分段线性模型,它学习了一个线性模型的集合,允许每个样本对象可以从中选择一个适合的线性映射。
其实模型主要的变换还是体现在兼容度评判函数中,其他的基本上沿用了ALE的设置,兼容度评判函数如下
(6) F ( x , y ) = max 1 ≤ i ≤ K w ~ i ⊤ ( x ⊗ y ) F(\mathbf{x}, \mathbf{y})=\max _{1 \leq i \leq K} \tilde{\mathbf{w}}_{i}^{\top}(\mathbf{x} \otimes \mathbf{y}) \tag 6 F(x,y)=1≤i≤Kmaxw~i⊤(x⊗y)(6)
其中 K ≥ 2 K\geq 2 K≥2, w ~ i ∈ R d x d y \tilde{\mathbf{w}}_{i} \in \mathbb{R}^{d_{x} d_{y}} w~i∈Rdxdy是模型其中一个线性模型的参数。可以重写成
(7) F ( x , y ) = max 1 ≤ i ≤ K x ⊤ W i y F(\mathbf{x}, \mathbf{y})=\max _{1 \leq i \leq K} \mathbf{x}^{\top} W_{i} \mathbf{y} \tag 7 F(x,y)=1≤i≤Kmaxx⊤Wiy(7)
前面提到的引入的隐变量其实就是用来选择线性模型的 i i i,损失函数同样是使用与SJE基本相同的基于排序的loss。
由于这种分段模型不是连续凸函数,用普通的SGD优化会有困难,所以这篇文章还提出了一个基于这个模型的SGD优化算法。
算法流程:
我们来分析一些它做了什么:
- 首先对于每个样本 ( x n , y n ) (\mathbf{x}_n,\mathbf{y}_n) (xn,yn),随机选择一个与 y n \mathbf{y}_n yn 不同的 y \mathbf{y} y (step 3);
- 如果选择的 y \mathbf{y} y 的兼容度与真实标签 y n \mathbf{y}_n yn 对应的兼容度的差距(有可能 y \mathbf{y} y 排在 y n \mathbf{y}_n yn 前,也有可能排在 y n \mathbf{y}_n yn后,但兼容度差距较小)小于设定的margin(文中取1,step 4),则需要更新模型(即映射矩阵 W W W );
- 如果需要更新模型,则具体做法如下:
- 找到一个 W i W_i Wi能够使得对于 y \mathbf{y} y 来说评分最高(step 5)
- 找到一个 W j W_j Wj 能够使得对于 y n \mathbf{y}_n yn来说评分最高(step 6)
- 如果两个矩阵相同,则与SJE一样更新权重(step 7-8)
- 如果两个矩阵不同,则更新各自选择的线性映射矩阵(step 10- 13)
这样的模型的好处除了上面说的有更强的表达能力之外,LatEm由于拥有多个 W W W,可以自适应地适应不同类型的样本,并且每个 W W W 会有不同的关注点。
上述介绍的方法,都是直接将视觉特征空间映射到语义空间来实现的,但是两个不同域的空间的语义差距较大,直接嵌入的效果仍不够理想,甚至会出现偏移。出于对齐两者空间、保持语义一致性的考虑,就有人提出了增加一个中间的共享空间(第三方空间),将两个空间都嵌入该空间里,并且同时进行优化以保持语义一致性。
4. 第三方空间
Zero-shot learning via semantic similarity embedding8(2015,ICCV)
这是比较经典的用到语义一致性的模型(SSE模型),它实现了上述的保持语义一致性,还在保持语义一致性的同时,保持分类准确性。我们来看它做了什么。
首先文章定义了
- 源域(source domain):每个类的语义描述
- 目标域(target domain):视觉图像特征 ( x n , y n ) (x_n,y_n) (xn,yn)
这其实就是我们说的语义空间和视觉特征空间,那么第三方空间是什么呢?
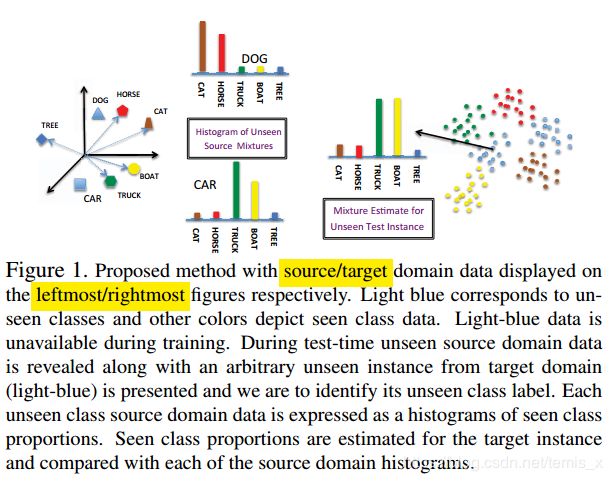
我个人把它理解为这个第三方空间是对源域和目标域的一个具有语义一致性的再表示,具体地说其实表现为一个直方图,文中的方法把source/target的实例都看作一个直方图(mixture),这个直方图是由已知类按比例组成的。如上图所示。而目标是使得表示同一个类的两个domain的直方图尽可能对齐。即假设 P P P 和 P y P_y Py 分别是unseen和seen类的条件目标特征分布,那么
(8) P = ∑ y ∈ S π ‾ y P y + P error P=\sum_{y \in \mathcal{S}} \overline{\pi}_{y} P_{y}+P_{\text { error }} \tag 8 P=y∈S∑πyPy+P error (8)
其中, π ‾ y \overline{\pi}_{y} πy 是组合中类y的权重,这样也有利于seen和unseen类之间的迁移。
如果要实现上述对齐两个domain的目标,那么很自然会有一个约束,这里设target的类 y y y的组合均值(average mixture,即中间空间)为 π ‾ y \overline{\pi}_{y} πy ,source对于类 y y y 的中间空间表示为 z y \mathbf{z}_y zy , 要求对于其他类别 y y y,即 y ≠ y ′ y\neq y' y̸=y′时,有
(9) ⟨ π ‾ y , z y ⟩ ≥ ⟨ π ‾ y , z y ′ ⟩ ⇔ ∑ s ∈ S ⟨ w , 1 N s ∑ i = 1 N I { y i = s } ϕ s ( x i ) ⟩ ( z y , s − z y ′ , s ) ≥ 0 \begin{array}{l}{\left\langle\overline{\boldsymbol{\pi}}_{y}, \mathbf{z}_{y}\right\rangle \geq\left\langle\overline{\boldsymbol{\pi}}_{y}, \mathbf{z}_{y^{\prime}}\right\rangle} \\ {\Leftrightarrow \sum_{s \in \mathcal{S}}\left\langle\mathbf{w}, \frac{1}{N_{s}} \sum_{i=1}^{N} \mathbb{I}_{\left\{y_{i}=s\right\}} \phi_{s}\left(\mathbf{x}_{i}\right)\right\rangle\left(z_{y, s}-z_{y^{\prime}, s}\right) \geq 0}\end{array} \tag 9 ⟨πy,zy⟩≥⟨πy,zy′⟩⇔∑s∈S⟨w,Ns1∑i=1NI{yi=s}ϕs(xi)⟩(zy,s−zy′,s)≥0(9)
这个式子的意思也就是上面说的“表示同一个类的两个domain的直方图尽可能对齐”,同一个类的必须大于或等于其他类别的。
目标函数
(10) min V , w , ξ , ϵ 1 2 ∥ w ∥ 2 + λ 1 2 ∑ v ∈ V ∥ v ∥ 2 + λ 2 ∑ y , s ϵ y s + λ 3 ∑ i , y ξ i y s.t. ∀ i ∈ { 1 , ⋯ , N } , ∀ y ∈ S , ∀ s ∈ S \begin{array}{l}{\min _{\mathcal{V}, \mathbf{w}, \xi, \epsilon} \frac{1}{2}\|\mathbf{w}\|^{2}+\frac{\lambda_{1}}{2} \sum_{\mathbf{v} \in \mathcal{V}}\|\mathbf{v}\|^{2}+\lambda_{2} \sum_{y, s} \epsilon_{y s}+\lambda_{3} \sum_{i, y} \xi_{i y}} \\ {\text { s.t. } \forall i \in\{1, \cdots, N\}, \forall y \in \mathcal{S}, \forall s \in \mathcal{S}}\end{array} \tag {10} minV,w,ξ,ϵ21∥w∥2+2λ1∑v∈V∥v∥2+λ2∑y,sϵys+λ3∑i,yξiy s.t. ∀i∈{1,⋯,N},∀y∈S,∀s∈S(10)
(11) ∑ i = 1 N I ( y i = y } N y [ f ( x i , y ) − f ( x i , s ) ] ≥ Δ ( y , s ) − ϵ y s \sum_{i=1}^{N} \frac{\mathrm{I}_{\left(y_{i}=y\right\}}}{N_{y}}\left[f\left(\mathbf{x}_{i}, y\right)-f\left(\mathbf{x}_{i}, s\right)\right] \geq \Delta(y, s)-\epsilon_{y s} \tag {11} i=1∑NNyI(yi=y}[f(xi,y)−f(xi,s)]≥Δ(y,s)−ϵys(11)
(12) f ( x i , y i ) − f ( x i , y ) ≥ Δ ( y i , y ) − ξ i y ϵ y s ≥ 0 , ξ i y ≥ 0 , ∀ v ∈ V , v ≥ 0 \begin{array}{l}{f\left(\mathbf{x}_{i}, y_{i}\right)-f\left(\mathbf{x}_{i}, y\right) \geq \Delta\left(y_{i}, y\right)-\xi_{i y}} \\ {\epsilon_{y s} \geq 0, \xi_{i y} \geq 0, \forall \mathbf{v} \in \mathcal{V}, \mathbf{v} \geq \mathbf{0}}\end{array} \tag {12} f(xi,yi)−f(xi,y)≥Δ(yi,y)−ξiyϵys≥0,ξiy≥0,∀v∈V,v≥0(12)
这是一个二次规划问题,其中Eq.10 中的 w \mathbf{w} w 是target domain的映射权重矩阵,而 V \mathcal{V} V 是source domain的,这两项起到正则的作用;而后面两项要结合Eq.2 和 Eq. 3来理解。
先来看Eq. 11 ,我们把 ϵ y s \epsilon_{y s} ϵys 移一下位置就很好理解了,即
(13) ϵ y s ≥ Δ ( y , s ) − ∑ i = 1 N I ( y i = y } N y [ f ( x i , y ) − f ( x i , s ) ] \epsilon_{y s} \geq\Delta(y, s)-\sum_{i=1}^{N} \frac{\mathrm{I}_{\left(y_{i}=y\right\}}}{N_{y}}\left[f\left(\mathbf{x}_{i}, y\right)-f\left(\mathbf{x}_{i}, s\right)\right] \tag {13} ϵys≥Δ(y,s)−i=1∑NNyI(yi=y}[f(xi,y)−f(xi,s)](13)
右边的形式就是我们上面熟悉的loss形式了,Eq. 12 也是一样的, ϵ y s \epsilon_{y s} ϵys 和 ξ i y \xi_{i y} ξiy 在这里是一个松弛变量。
那么Eq. 11 和 Eq. 12 具体是什么,区别在哪。首先来看Eq. 10 中的 s ∈ S s \in \mathcal{S} s∈S,表示语义空间;而 y y y就是标签。那么Eq. 11 就是用来衡量alignment loss的(即语义一致性的对齐),而Eq. 12 是衡量classification loss的(即分类)。
这样做有什么好处,看下面这张图
如果只考虑两个domain对齐,则有可能会造成误分类的情况,即图(a);而如果只考虑分类的话,则可能没有完全对齐分布,即图(b);所以本文的方法同时考虑了两者,既对齐分布又考虑分类,图©。
5. ZSL中存在的问题
在介绍下面的模型之前,我们先来介绍一下ZSL中存在的一些问题。
1)领域漂移问题(domain shift)
Transductive Multi-View Zero-Shot Learning9(2015,TPAMI)
领域漂移问题是2015年正式提出的。从直观上解释,就是同一种属性,在不同的类别中,视觉特征的表现可能会不一样。例如像这篇文章中举的例子,如图,斑马和猪都有一个属性是“有尾巴”,而这两者的尾巴在视觉特征中却相去甚远。如果斑马是训练集,而猪是测试集,那么利用斑马训练出来的模型,则很难正确地对猪进行分类。因为可能在训练集中的数据对“有尾巴”的描述与测试集中的不一样,虽然它们都有“有尾巴”这个属性,这样直接迁移可能会有偏差。
这篇文章也针对这个问题提出了一个解决方法,但后面用的比较多的解决方法还是SAE10模型中的方法,下面我来介绍一下这种方法。
Semantic Autoencoder for Zero-Shot Learning(2017,CVPR)
SAE模型的解决方案是增加了一个额外的条件限制,即语义嵌入时必须保持原始视觉特征的所有信息,即它们是可以被重构的。具体的,
目标函数就变成了
(14) min w , W ∗ ∥ X − W ∗ W X ∥ F 2 s.t. W X = S \min _{\mathbf{w}, \mathbf{W}^{*}}\left\|\mathbf{X}-\mathbf{W}^{*} \mathbf{W} \mathbf{X}\right\|_{F}^{2} \quad \text { s.t. } \quad \mathbf{W X}=\mathbf{S} \tag{14} w,W∗min∥X−W∗WX∥F2 s.t. WX=S(14)
简单起见,我们让 W ∗ = W T W^*=W^T W∗=WT,即目标函数可重写成:
(15) min W ∥ X − W ⊤ W X ∥ F 2 s.t. W X = S \min _{\mathbf{W}}\left\|\mathbf{X}-\mathbf{W}^{\top} \mathbf{W} \mathbf{X}\right\|_{F}^{2} \quad \text { s.t. } \quad \mathbf{W X}=\mathbf{S} \tag{15} Wmin∥∥X−W⊤WX∥∥F2 s.t. WX=S(15)
即
(16) min W ∥ X − W ⊤ S ∥ F 2 s.t. W X = S \min _{\mathbf{W}}\left\|\mathbf{X}-\mathbf{W}^{\top} \mathbf{S}\right\|_{F}^{2} \quad \text { s.t. } \quad \mathbf{W X}=\mathbf{S} \tag{16} Wmin∥∥X−W⊤S∥∥F2 s.t. WX=S(16)
但是这样的目标函数有一个比较强的约束: W X = S WX=S WX=S,会导致优化困难,所以文中做了一个变换,变成一个松一点的软约束:
(17) min W ∥ X − W ⊤ S ∥ F 2 + λ ∥ W X − S ∥ F 2 \min _{\mathbf{W}}\left\|\mathbf{X}-\mathbf{W}^{\top} \mathbf{S}\right\|_{F}^{2}+\lambda\|\mathbf{W} \mathbf{X}-\mathbf{S}\|_{F}^{2} \tag{17} Wmin∥∥X−W⊤S∥∥F2+λ∥WX−S∥F2(17)
这样问题变成了凸优化问题,容易优化。
文中还做了进一步的转换:
由于迹 T r ( X ) = T r ( X T ) , T r ( W T S ) = T r ( S T W ) Tr(X)=Tr(X^T),\ Tr(W^TS)=Tr(S^TW) Tr(X)=Tr(XT), Tr(WTS)=Tr(STW) ,则
(18) min W ∥ X ⊤ − S ⊤ W ∥ F 2 + λ ∥ W X − S ∥ F 2 \min _{\mathbf{W}}\left\|\mathbf{X}^{\top}-\mathbf{S}^{\top} \mathbf{W}\right\|_{F}^{2}+\lambda\|\mathbf{W} \mathbf{X}-\mathbf{S}\|_{F}^{2} \tag{18} Wmin∥∥X⊤−S⊤W∥∥F2+λ∥WX−S∥F2(18)
那么要求解这个问题,对上面这个式子求导,并使其导数为0,即
(19) − S ( X ⊤ − S ⊤ W ) + λ ( W X − S ) X ⊤ = 0 S S ⊤ W + λ W X X ⊤ = S X ⊤ + λ S X ⊤ \begin{array}{c}{-\mathbf{S}\left(\mathbf{X}^{\top}-\mathbf{S}^{\top} \mathbf{W}\right)+\lambda(\mathbf{W} \mathbf{X}-\mathbf{S}) \mathbf{X}^{\top}=0} \\ {\mathbf{S S}^{\top} \mathbf{W}+\lambda \mathbf{W} \mathbf{X} \mathbf{X}^{\top}=\mathbf{S} \mathbf{X}^{\top}+\lambda \mathbf{S} \mathbf{X}^{\top}}\end{array} \tag{19} −S(X⊤−S⊤W)+λ(WX−S)X⊤=0SS⊤W+λWXX⊤=SX⊤+λSX⊤(19)
如果设 A = S S T , B = λ X X T , C = ( 1 + λ ) S X T A=SS^T,\ B=\lambda XX^T,\ C=(1+\lambda)SX^T A=SST, B=λXXT, C=(1+λ)SXT,那么上面的式子可以变成:
(20) A W + W B = C AW+WB=C \tag{20} AW+WB=C(20)
这个形式就是著名的 Sylvester equation (西尔维斯特方程),可以简单高效地求解。
SAE这个额外的限制很大程度地解决了领域漂移的问题,文中说这是因为虽然从seen到unseen的属性的视觉表达会有所改变,但是视觉特征对更真实的要求是两者通用的,这能使嵌入时更少地遭受领域漂移的影响。
还有一种解决领域漂移的方法是生成模型,例如GlaP11模型;它学习了两个域的分布(原型),这样就可以从分布中生成unseen类的虚拟实例,来解决领域漂移的问题。
而对于“生成”模型,很自然就想到了GAN,这是基于一个很自然的想法:我们人看到一段文字的时候,如果之前没见过所描述的对象,我们首先会在脑海中先形成一种模糊的想象,这种想象与真实的肯定会有一定的偏差,但是修正想象比直接从文本描述就能得到真实的对象更加容易。而GAN在这里就充当“想象”这一过程。
然后我去搜了相关工作,还真的有人把GAN和零次学习放在一起做,非常典型的一篇文章就是
A Generative Adversarial Approach for Zero-Shot Learning from Noisy Texts12(2018,CVPR)
这篇文章就是把ZSL转换成了一个Imagination Problem,通过一个条件GAN来合成视觉特征(这里不是合成图像),并且在保证unseen类的类间区分性的同时,还保证了合成的数据实例具有类内多样性。
我个人觉得这种“想象”的方法是一个很合理的解决方案,更接近所谓的“本质”。
2) 语义间隔问题(Semantic Gap)
ZSL存在的另一个问题则是语义间隔问题,它是指样本在特征空间中所构成的流形(分布结构)与样本在语义空间中类别构成的流形是不一致的,这使得直接学习两者的映射会有困难。比较简单的解决方法有
Zero-Shot Recognition using Dual Visual-Semantic Mapping Paths13(2017,CVPR)
它的做法是基于流形学习的,对语义进行再表示,并且迭代地调整,以对齐两者的流形。
另外值得注意的是这篇文章是直推式的零次学习。
6. 直推式学习(Transductive Zero-shot Learning)
所谓直推式学习,即在ZSL中,训练模型的时候,我们可以拿到测试集的数据,只是不能拿到测试集的样本的标签,因此我们可以利用测试集数据,得到一些测试集类别的先验知识。这种设置在迁移学习中很常见。
Semi-supervised vocabulary-informed learning14(2016,CVPR)
这篇文章是一个半监督问题,也是一个直推式零次学习问题。这样的设置的合理性在于,非直推式学习通常有以下几个缺点:
- 它假定unseen类不能被错误地分类为seen类,反之亦然。这会很大程度且不现实地简化了问题。
- unseen的候选标签集通常相对小,与人类的识别能力相比相差很远。
- seen类需要大量的数据。
- 语义知识中的大量开集词汇(作为ZSL的一部分),不会以任何方式让模型知道它的存在,即inform the learning or recognition。
对于第1点可以通过类增量学习的方式解决,例如,如果我们通过看图像实例来学习car这个概念,当不知道世界上还有其他的motor vehicle存在时,很可能把有4个轮子的都称为car。这样的话,进行零次学习时,truck与car可能会有很高的相似度。然而,想象一下如果知道许多其他的motor vehicles(trucks,mini-vans等),即使没有见过这些车,但关于它们的一些基础知识可以获得,并且这些知识与car密切相关,这足以把其他vehicle跟car区分开来,所以这时原则上应该对car的识别规则进行更新,使对car的识别更加的严谨。
而第2和3点需要大量人工代价,而本文针对第4点提出了一个半监督方法。具体地,假设我们有少量标签训练数据和大量开集的vocabulary/semantic 词典(以文本形式表现,从这些词典中可以学习到词汇原型间的语义联系)。目标是是学习一个模型,该模型可以利用语义词典,来帮助更好地训练seen类别和unseen类别的分类器。不同于常规的半监督,我们没有假设无标签的数据是可用的,只有unseen类它们的vocabulary是可用的。
设 W s \mathcal{W}_{s} Ws、 W t \mathcal{W}_{t} Wt 分别是seen和unseen的标签集,每个标签表示为 z ∈ W z \in \mathcal{W} z∈W ,语义嵌入空间的语义向量(又叫类原型)为 u \mathbf{u} u.
嵌入学习
Data Term
有两种学习形式,最简单的目标函数就是常用的岭回归,文中把这种方法归为Data Term。
L ( x i , u z i ) = ∥ W T x i − u z i ∥ 2 2 + λ ∥ W ∥ F 2 \mathcal{L}\left(\mathbf{x}_{i}, \mathbf{u}_{z_{i}}\right)=\left\|W^{T} \mathbf{x}_{i}-\mathbf{u}_{z_{i}}\right\|_{2}^{2}+\lambda\|W\|_{F}^{2} L(xi,uzi)=∥∥WTxi−uzi∥∥22+λ∥W∥F2
但是这种方法只解决了seen样本的嵌入问题,没有用到unseen数据的相关信息。于是文中提出了Pairwise Term的形式,下面来介绍它是怎么使用unseen的语义词典的。
Pairwise Term
我们根据从unseen的语义词典可以拿到unseen类别的类原型(即语义向量),但是我们的训练图像样本却只有seen类的,那么如果把这些样本的视觉特征投影到unseen的类原型中,这显然是不对的;所以这些样本距离它自己对应的类原型更近的同时,也要尽可能远离unseen的类原型。也就是对于嵌入过程增加了一定的margin来限制。因为考虑了两者情况,所以才叫Pairwise Term吧。
上面的想法用数学语言来描述即
(21) M V ( x i , u z i ) = 1 2 ∑ a = 1 A V [ C + 1 2 D ( x i , u z i ) − 1 2 D ( x i , u a ) ] + 2 \mathcal{M}_{V}\left(\mathbf{x}_{i}, \mathbf{u}_{z_{i}}\right)=\frac{1}{2} \sum_{a=1}^{A_{V}}\left[C+\frac{1}{2} D\left(\mathbf{x}_{i}, \mathbf{u}_{z_{i}}\right)-\frac{1}{2} D\left(\mathbf{x}_{i}, \mathbf{u}_{a}\right)\right]_{+}^{2} \tag{21} MV(xi,uzi)=21a=1∑AV[C+21D(xi,uzi)−21D(xi,ua)]+2(21)
其中, a ∈ W t a \in \mathcal{W}_{t} a∈Wt 是从open vacabulary中选择的, C C C是margin gap, [ ⋅ ] t 2 [\cdot]_{t}^{2} [⋅]t2 是我们熟悉的hinge loss。这个式子的意思是对于x的注入,距离它自己正确类别的类原型的距离 D ( x i , u z i ) D\left(\mathbf{x}_{i}, \mathbf{u}_{z_{i}}\right) D(xi,uzi) 要比与unseen类的类原型的距离 D ( x i , u a ) D\left(\mathbf{x}_{i}, \mathbf{u}_{a}\right) D(xi,ua) 小。
为了加速计算,与距离seen的类原型最近的unseen类原型 u b \mathbf{u}_b ub比较即可,即从unseen的类原型中挑了最接近seen的比较,拉开它们的距离即可:
(22) M S ( x i , u z i ) = 1 2 ∑ b = 1 B S [ C + 1 2 D ( x i , u z i ) − 1 2 D ( x i , u b ) ] + 2 \mathcal{M}_{S}\left(\mathbf{x}_{i}, \mathbf{u}_{z_{i}}\right)=\frac{1}{2} \sum_{b=1}^{B_{S}}\left[C+\frac{1}{2} D\left(\mathbf{x}_{i}, \mathbf{u}_{z_{i}}\right)-\frac{1}{2} D\left(\mathbf{x}_{i}, \mathbf{u}_{b}\right)\right]_{+}^{2} \tag{22} MS(xi,uzi)=21b=1∑BS[C+21D(xi,uzi)−21D(xi,ub)]+2(22)
那么完整的margin项即为
(23) M ( x i , u z i ) = M V ( x i , u z i ) + M S ( x i , u z i ) \mathcal{M}\left(\mathbf{x}_{i}, \mathbf{u}_{z_{i}}\right)=\mathcal{M}_{V}\left(\mathbf{x}_{i}, \mathbf{u}_{z_{i}}\right)+\mathcal{M}_{S}\left(\mathbf{x}_{i}, \mathbf{u}_{z_{i}}\right) \tag{23} M(xi,uzi)=MV(xi,uzi)+MS(xi,uzi)(23)
而完整的目标函数应该由Data Term 和 Pairwise Term 组合而成,两者分别考虑了不同的方面:
(24) ∑ i = 1 n T ( α L ϵ ( x i , u y i ) + ( 1 − α ) M ( x i , u z i ) ) + λ ∥ W ∥ F 2 \sum_{i=1}^{n T}\left(\alpha \mathcal{L}_{\epsilon}\left(\mathbf{x}_{i}, \mathbf{u}_{y_{i}}\right)+\right.(1-\alpha) \mathcal{M}\left(\mathbf{x}_{i}, \mathbf{u}_{z_{i}}\right) )+\lambda\|W\|_{F}^{2} \tag{24} i=1∑nT(αLϵ(xi,uyi)+(1−α)M(xi,uzi))+λ∥W∥F2(24)
以上的模型其实都或多或少依赖于额外的辅助信息(属性、词向量等)来建立seen类和unseen类之间的迁移,于是就有人想能不能不使用额外的辅助信息来实现零次学习呢?答案是肯定的,虽然效果可能不如使用辅助信息,但是作为一种探索还是非常有意义的。
7. 不使用额外的辅助信息
这里介绍一篇早期的探索,后面这样做的工作相对较少。
Metric learning for large scale image classification: Generalizing to new classes at near-zero cost15(2012,ECCV)
这篇文章借鉴了聚类和度量学习的方法,并且探索了两种方法:KNN和NCM。
它用每个类的类中心(KNN)/类均值(NCM)来取代ZSL中对于每个类的语义描述,然后学习一个度量,使得它们在seen和unseen类间共享,达到迁移的效果。
后面有个Few-shot的工作的做法跟这个有点相似,2018年CVPR的Learning to Compare: Relation Network for Few-Shot Learning16。
8. ZSL中的特征提取
ZSL中大多数工作都在关注Visual-Semantic 的嵌入问题,而少有工作去关注模型提取特征,甚至既关注嵌入问题又关注特征提取,下面我来介绍一些零次学习中更细一点的工作,这是一篇从整体上(既考虑特征提取又考虑嵌入问题)考虑ZSL问题的工作。
Discriminative Learning of Latent Features for Zero-Shot Recognition17(2018,CVPR)
LDF模型
Motivation
首先,我们都认可一个事实:无论是模型为了分类提取的特征还是从文本描述中提取的语义特征我们都希望是discriminative的,而ZSL中通常都是用预训练好的CNN来直接提取出特征来完成ZSL任务,这种预训练模型提取的特征直接用在我们的数据集上可能不是最优的,因为预训练的模型训练时的目标任务并不是零次学习任务。
其次,有些discriminative的视觉特征也许会没有反映在预定义的属性上。
最后,视觉特征提取和语义嵌入如果是两个独立训练的过程,对于整个问题的求解也许不是最优的。
基于以上这三点存在的问题,本文针对ZSL任务提出了一个基于级联结构的学习隐式区分性特征的模型。怎么做?
(声明:这篇文章虽然是级联结构,但其实只放缩了一次,即只使用了两种尺度。)
对于每个尺度的图像,都会经过三个组件的处理,如下图:
- FNet 提取图像特征;
- ZNet定位最具区分性的区域,然后缩放到一个更大的尺度,继续提取更具区分性的区域;
- ENet构建嵌入空间,在该空间里视觉与语义信息是有关联的。
-
FNet
本文考虑两个变体:VGG19和GoogLeNet,用来提取图片特征;
不同于传统的ZSL方法,FNet的参数是与其他组件联合训练的,所以获取的特征会更对接下来的一些组件工作更有帮助。
-
ZNet
目前有研究表明,从(只包含)目标区域中学习更有利于图片级别的分类。
另一方面,ZSL的候选区域需要反映一些人工定义的属性,其中就有一些背景,例如树、山等。因此,ZSL这个目标区域(object-centric region)又期望是包含一些背景的,以提高属性嵌入性能。
本文提出的ZNet可以自动从粗到细粒度搜索合适的discriminative区域。
因此,一个合适ZSL任务的目标区域应该是:对分类是discriminative,同时又能与标记的属性相匹配。
具体地,ZNet其实由**两层全连接层+sigmoid(有点像SE,或许可以看成一个注意力机制)**组成,找到最具区分性的区域后对其进行放大到原图像尺寸。
-
ENet
这个组件其实就跟常规的ZSL的嵌入设置差不多,但是对嵌入空间做了一些增强。因为基于人工定义的属性嵌入,通常表达能力有限,规模也有限,而且属性通常都不是对于任务discriminative的。
这篇文章提出一个增强的属性空间。在这个空间里,图像会被嵌入由**人工定义属性(UA)和隐式区分性属性(latent discriminative attributes,LA)**构成的空间里。
最后的目标函数也会由这两部分组成,即对于两个尺度( s 1 , s 2 s_1,s_2 s1,s2)的网络,整个LDF模型的loss为
(25) L = L a t t s 1 + L l a t s 1 + L a t t s 2 + L l a t s 2 \mathcal{L}=\mathcal{L}_{\mathrm{att}}^{s 1}+\mathcal{L}_{\mathrm{lat}}^{s 1}+\mathcal{L}_{\mathrm{att}}^{s 2}+\mathcal{L}_{\mathrm{lat}}^{s 2} \tag{25} L=Latts1+Llats1+Latts2+Llats2(25)
其中, L a t t \mathcal{L}_{\mathrm{att}} Latt 表示人工定义属性的, L l a t \mathcal{L}_{\mathrm{lat}} Llat 表示学习而来的隐式区分性属性的。
Xian Y, Lampert C H, Schiele B, et al. Zero-Shot Learning - A Comprehensive Evaluation of the Good, the Bad and the Ugly[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018: 1-1. ↩︎
C. H. Lampert, H. Nickisch, and S. Harmeling. “Learning To Detect Unseen Object Classes by Between-Class Attribute Transfer”. In CVPR, 2009 ↩︎
Akata Z, Perronnin F, Harchaoui Z, et al. Label-Embedding for Attribute-Based Classification[C]. computer vision and pattern recognition, 2013: 819-826. ↩︎
Weston J, Bengio S, Usunier N, et al. WSABIE: scaling up to large vocabulary image annotation[C]. international joint conference on artificial intelligence, 2011: 2764-2770. ↩︎
Frome A, Corrado G S, Shlens J, et al. DeViSE: A Deep Visual-Semantic Embedding Model[C]. neural information processing systems, 2013: 2121-2129. ↩︎
Akata Z, Reed S, Walter D, et al. Evaluation of output embeddings for fine-grained image classification[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015: 2927-2936. ↩︎
Xian Y, Akata Z, Sharma G, et al. Latent embeddings for zero-shot classification[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 69-77. ↩︎
Zhang Z, Saligrama V. Zero-shot learning via semantic similarity embedding[C]//Proceedings of the IEEE international conference on computer vision. 2015: 4166-4174. ↩︎
Fu Y, Hospedales T M, Xiang T, et al. Transductive multi-view zero-shot learning[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(11): 2332-2345. ↩︎
Kodirov E, Xiang T, Gong S. Semantic autoencoder for zero-shot learning[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017: 3174-3183. ↩︎
Li Y, Wang D. Zero-shot learning with generative latent prototype model[J]. arXiv preprint arXiv:1705.09474, 2017. ↩︎
Zhu Y, Elhoseiny M, Liu B, et al. A generative adversarial approach for zero-shot learning from noisy texts[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 1004-1013. ↩︎
Li Y, Wang D, Hu H, et al. Zero-shot recognition using dual visual-semantic mapping paths[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017: 3279-3287. ↩︎
Fu Y, Sigal L. Semi-supervised vocabulary-informed learning[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 5337-5346. ↩︎
Mensink T, Verbeek J, Perronnin F, et al. Metric learning for large scale image classification: Generalizing to new classes at near-zero cost[M]//Computer Vision–ECCV 2012. Springer, Berlin, Heidelberg, 2012: 488-501. ↩︎
Sung F, Yang Y, Zhang L, et al. Learning to compare: Relation network for few-shot learning[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 1199-1208. ↩︎
Li Y, Zhang J, Zhang J, et al. Discriminative learning of latent features for zero-shot recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 7463-7471. ↩︎