MR-GNN: Multi-Resolution and Dual Graph Neural Network for Predicting Structured Entity Interactions
论文地址:MR-GNN: Multi-Resolution and Dual Graph Neural Network for Predicting Structured Entity Interactions
这篇论文被IJCAI 2019接收,主要工作是在用GNN预测分子间相互作用的任务上,引入了LSTM对两个分子不同层的表示进行编码,从而在获得不同的receptive field(RF)的信息的基础上得到两个分子之间的交互信息。
Motivation
传统的图神经网络的receptive field是固定的,例如一个三层的GCN能聚合中心节点周围三跳的邻居节点的信息,但是这样具有一定的局限性

左侧是对苯二酚,右侧是乙酸,蓝框中的部分是判定它们是酸的重要标志。左侧的蓝框是红色节点的三跳邻域,而右侧是红色节点的两跳邻域,所以统一地使用三层或两层的GCN不能很好地提取出有效的信息。
并且,在预测分子间相互作用时,发生作用的分子结构的大小也可能不同。在酸碱中和过程中,碱基可以通过乙酸的第二卷积层的特征来精确地模拟它们之间的相互作用,而对苯二酚,最好的选择是通过第三个卷积层的特征来对其相互作用进行建模。因此,在预测时需要考虑这两个分子不同RF的特征。
Method
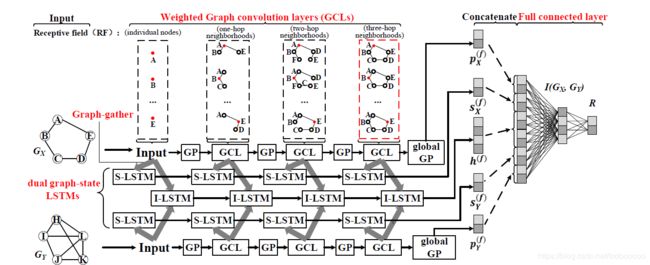
graph convolution layer
为了区分不同度的节点在聚合信息时的重要程度,模型在聚合过程中使用了度相关的权重矩阵: f i ′ ( t + 1 ) = f i ( t ) Φ d i ( t ) + ∑ v j ∈ N i f j ( t ) Ψ d i ( t ) + b d i ( t ) f_{i}^{\prime(t+1)}=f_{i}^{(t)} \Phi_{d_{i}}^{(t)}+\sum_{v_{j} \in N_{i}} f_{j}^{(t)} \Psi_{d_{i}}^{(t)}+b_{d_{i}}^{(t)} fi′(t+1)=fi(t)Φdi(t)+vj∈Ni∑fj(t)Ψdi(t)+bdi(t) Φ \Phi Φ和 Ψ \Psi Ψ分别是节点自己的权重矩阵和邻居的权重矩阵。 d i d_i di是节点 i i i的度。
在聚合信息过后,还要再经过一个Graph Pooling层,通过对邻居节点的表示和自己的表示逐位取最大值得到最终的表示。 f i ( t + 1 ) = G P ( f i ′ ( t + 1 ) , { f j ′ ( t + 1 ) } v j ∈ N i ) f_{i}^{(t+1)}=G P\left(f_{i}^{\prime(t+1)},\left\{f_{j}^{\prime(t+1)}\right\}_{v_{j} \in N_{i}}\right) fi(t+1)=GP(fi′(t+1),{fj′(t+1)}vj∈Ni)
graph-gather layer
通过对图中所有节点做线性变换再累积求和后得到整张图的一个表示: g ( t ) = ∑ 1 ≤ i ≤ m f i ( t ) Θ d i ( t ) + β d i ( t ) g^{(t)}=\sum_{1 \leq i \leq m} f_{i}^{(t)} \Theta_{d_{i}}^{(t)}+\beta_{d_{i}}^{(t)} g(t)=1≤i≤m∑fi(t)Θdi(t)+βdi(t)
dual graph-state lstms
首先引入Summary-LSTM(S-LSTM)来聚合同一个图上不同层的表示 s ( t + 1 ) = L S T M ( s ( t ) , g ( t ) ) s^{(t+1)}=LSTM(s^{(t)},g^{(t)}) s(t+1)=LSTM(s(t),g(t))为了更好地表示图上的信息,又将S-LSTM最后的隐藏层和整张图最后一层的pooling的结果拼接在一起,最终得到整张图的表示: e ( f ) = [ s ( f ) , p ( f ) ] e^{(f)}=[s^{(f)}, p^{(f)}] e(f)=[s(f),p(f)] p ( f ) = G P ( f v 1 ( f ) , … , f v m ( f ) ) ∈ R 1 × c f p^{(f)}=G P\left(f_{v_{1}}^{(f)}, \ldots, f_{v_{m}}^{(f)}\right) \in \mathbb{R}^{1 \times c_{f}} p(f)=GP(fv1(f),…,fvm(f))∈R1×cf更进一步地,使用Interaction-LSTM(I-LSTM)来获得两张图之间相互作用的信息 h ( t + 1 ) = LSTM ( h ( t ) , [ g X ( t ) , g Y ( t ) ] ) h^{(t+1)}=\operatorname{LSTM}\left(h^{(t)},\left[g_{X}^{(t)}, g_{Y}^{(t)}\right]\right) h(t+1)=LSTM(h(t),[gX(t),gY(t)])输入是图 X X X和图 Y Y Y的表示。
fully connected layer
最后将向量拼接起来,然后经过全连接层和softmax进行分类预测。 I ( G X , G Y ) = [ e X ( f ) , e Y ( f ) , h ( f ) ] I\left(G_{X}, G_{Y}\right)=\left[e_{X}^{(f)}, e_{Y}^{(f)}, h^{(f)}\right] I(GX,GY)=[eX(f),eY(f),h(f)]