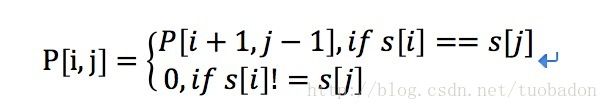Longest Palindromic Substring 最长回文串 python实现

一、  题目：

输入字符串s,输出该字符串中包含的最长回文串。回文串，指的是正着看和倒着看都一样的字符串，例如’abdba’。

二、几种解法

1、      Brute-force解法

(1)、思路：

第一步，通过两层for循环得到输入字符串s的所有可能子串。

第二步，逐个判断子串是否为回文串。若当前子串为回文串且长度大于之前得到的回文串，更新当前最长回文串。

(2)、代码

'''
Brute-force解法
'''
class Solution1(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        lens=len(s)
        if lens<2:
            return s
        maxlen=0
        start=0
        for i in range(lens):
            for j in range(i+1,lens):
                begin=i
                end=j
                while begin=end and j-i>maxlen:
                    maxlen=j-i+1
                    start=i
        if maxlen>0:
            return s[start:maxlen]
        return None

(3)、复杂度分析:

时间复杂度：

得到字符串所有子串的时间复杂度为O(n^2),判断子串是否为回文串的时间复杂度为O(n),二者相乘得到暴力解法的时间复杂度为O(n^3).

空间复杂度:

该方法没有使用额外空间,空间复杂度为O(n)

2、      动态规划方法

(1)、思路：

子问题:

      以i开始,以j结束的子串的最长回文串

状态：

      令P[i,j]表示：以i开始,以j结束的子串是否为回文串。其值为0,1。P[i,j]==0表示子串s[i:j]不是回文串，P[i,j]==1表示子串s[i:j]是回文串。

 

状态转移方程：

   

 

终止条件:

      遍历完所有子串

(2)、代码

'''
动态规划解法：
dp数组：维护子串状态
step 1:初始化dp数组,完成长度小于3的子串状态判断
step 2:i为子串长度，j为子串起始地址，r为子串结束地址.
第二步逐步得到长度为i的子串状态，利用状态转移方程完成这一判断。
step 3:根据第二步得到的最长子串长度和起始位置，得到最终结果
'''
class Solution2(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        if not s:
            return None
        lens=len(s)
        if lens<2:
            return s
        maxlen=0
        start=0
        dp=[[0]*lens]*lens

        #step 1
        for i in range(lens):
            dp[i][i]=True
            if i=2:
            return s[start:start+maxlen]
        return None

(3)、算法复杂度分析：

时间复杂度：

得到字符串所有子串的时间复杂度为O(n^2),判断子串是否为回文串的时间复杂度为O(1),二者相乘得到动态规划法的时间复杂度为O(n^2).

空间复杂度:

该方法需要额外的空间维护dp数组，空间复杂度为O(n^2)。

3、      中心扩展法

(1)、思路：

step 1:遍历每个字符,把每个字符当做中心逐步向两边扩展,每扩展一步就得到一个新的子串。这里针对输入字符串的长度，扩展方式需要根据长度奇偶性质做判断。

Step 2:判断子串是否为回文串，更新当前最长回文串

Step 3:返回最长回文串

(2)、代码:

'''
中心扩展法
step 1:遍历每个字符,把每个字符当做中心逐步向两边扩展,每扩展一步就得到一个新的子串。
这里针对输入字符串的长度，扩展方式需要根据长度奇偶性质做判断。
Step 2:判断子串是否为回文串，更新当前最长回文串
Step 3:返回最长回文串
'''
class Solution3(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        lens=len(s)
        maxlen=0
        start=0

        # 长度为奇数
        for i in range(lens):
            j = i - 1
            k = i + 1
            while j >= 0 and k < lens and s[j] == s[k]:
                if k - j + 1 > maxlen:
                    maxlen = k - j + 1
                    start = j
                j -= 1
                k += 1

        # 长度为偶数
        for i in range(lens):
            j = i
            k = i + 1
            while j >= 0 and k < lens and s[j] == s[k]:
                if k - j + 1 > maxlen:
                    maxlen = k - j + 1
                    start = j
                j -= 1
                k += 1

        if maxlen>0:
            return s[start:start+maxlen]
        return None

(3)、算法复杂度分析：

时间复杂度：

遍历字符串的时间复杂度为O(n),中心扩展及判断子串是否为回文串的时间复杂度为O(n),二者相乘得到动态规划法的时间复杂度为O(n^2).

空间复杂度:

该方法没有使用额外的空间，空间复杂度为O(n)。

4、      manacher算法

(1)、思路：

算法主要解决两个问题：

问题一：长度奇偶性带来的对称轴位置问题

       解决办法就是字符串内插入特殊字符'#'，处理后字符串长度为奇数。

问题二：重复访问的问题

解决办法是计算字符i回文半径时尽量利用之前回文串匹配的结果，减少重复字符比对。

利用上次匹配结果部分，涉及到的变量有：存储字符i回文半径的数组P，上一个回文串的中心位置c以及回文串结束位置r。

如果本次字符位置i小于上一个回文串结束位置r,那么上一个回文串与以i为中心的回文串有重复部分，重复部分的利用需要参考当前字符关于中心c的对称位置i’,同时需要考虑不要超出上个回文串的结束位置。如果没有重复部分可以利用，那么不断中心扩展。

(2)、代码：

'''
Manacher算法:
step 1: 字符串内插入特殊字符'#'，处理后字符串长度为奇数；字符串收尾插入特殊字符，避免数组越界
step 2:逐个遍历字符，计算得到以每个字符为中心的最长回文串半径。
涉及到的变量有：存储字符i回文半径的数组P，上一个回文串的中心位置c以及回文串结束位置r。
计算字符i回文半径：本次计算尽量利用之前回文串匹配的结果，减少重复字符比对。
'''
class Solution4(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        if not s:
            return None
        if len(s)<2:
            return s
        T='#'.join('@{}$'.format(s))#step 1
        #step2
        n=len(T)
        P=[0]*n
        c=0
        r=0
        for i in range(1,n-1):
            i_mirror=c-(i-c)#i关于中心c的对称位置
            if r>i:#利用之前回文串字符对比重复部分
                P[i]=min(r-i,P[i_mirror])
            # 中心扩展法完成之前没有涉及的字符比对
            while T[i+1+P[i]]==T[i-1-P[i]]:
                P[i]=P[i]+1
            #更新当前回文串中心c及终止位置r
            if i+P[i]>r:
                c=i
                r=i+P[i]
        #找到最大回文半径及对应的回文中心
        maxlen=0
        centeridx=0
        for i in range(1,n-1):
            if P[i]>maxlen:
                maxlen=P[i]
                centeridx=i
        #获取最长回文串
        begin=(centeridx-maxlen)//2
        end=(centeridx+maxlen)//2
        return s[begin:end]

(3)、算法复杂度分析：

时间复杂度：

      遍历字符串的时间复杂度为O(n), 只对尚未匹配的部分进行中心扩展的时间复杂度为O(1),二者相乘得到动态规划法的时间复杂度为O(n).

空间复杂度:

      该方法没有使用额外的空间，空间复杂度为O(n)。

 

参考博客：

[1] https://articles.leetcode.com/longest-palindromic-substring-part-ii/

[2] https://segmentfault.com/a/1190000003914228

[3] http://blog.csdn.net/kangroger/article/details/37742639