编译原理总结

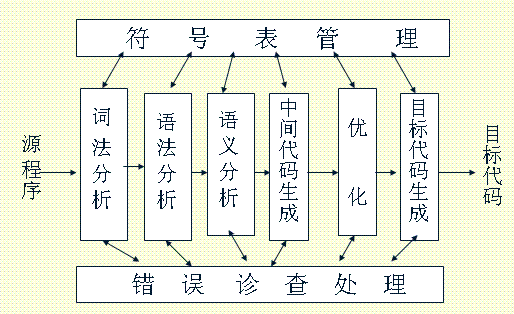
一、编译程序架构

二、词法分析

从左至右扫描字符序列，识别出单词(关键字、标示符、常数、特殊符号)。

三、语法分析

按照语言语法的规则，将词法分析所得的单词分解为各个语法成分。(分析单词串是否构成短语和句子)

四、 语义分析：

源程序进行上下文有关性质的检查，看源程序有无语义错误。例如：变量是否定义、类型是否正确

五、中间代码生成

含义明确、便于处理的记号系统。这种记号系统于源程序和机器语言之间，容易将它翻译成目标代码。如三元式、四元式、逆波兰式等

六、中间代码优化：

有局部优化、循环优化和全局优化。主要方法有代码外提、强度削弱、删除归纳变量等。

七、目标代码生成：

针对具体设备进行汇编优化等。

文法

文法
①.文法的定义：对语言结构的定义和描述。例如，“The cat ate a house”。

②.文法的组成：
⑴.终结符：用小写字母表示，记为VT。
⑵.非终结符：用大写字母表示，记为VN。
⑶.文法规则集合：规则一般表示为：A->a。
一个形式文法是四元有序组G = (VN, VT, S, P)。其中，S为文法的开始符号，P是规则集。很显然，见下图：

举个例子，设VN={A},VT={a,b,c},S=A,P={A->aAb, A->c}。这样就构成了文法G = ({A}, {a,b,c}, A, P)。

③.文法的分类：0型文法，1型文法，2型文法，3型文法。

              0型文法：也叫短语结构文法。辨别依据：当有α->β时，左边α中必须含有非终结符，形如A->β等。
              1型文法：也叫上下文有关文法。辨别依据：在0型文法的基础上，当有α->β时，定有
|α| <= |β|，其中|α| 和|β|分别表示其长度。如有A->Ba,则|α|=1，|β|=2符合1型文法要求。反之,如aA->a，则不符合1型文法。
              附注：虽然要求|α| <= |β|，但有一特例：α->ε也满足1型文法。
              2型文法：也叫上下文无关文法。辨别依据：在1型文法的基础上，当有α->β时，α必是非终结符。如A->Ba,符合2型文法要求。 如果是Aa->Ba这样的形式，那么就不满足了，因为Aa不是一个非终结符。
              3型文法：也叫正则文法。辨别依据：在2型文法的基础上需满足：A->a|aB（右线性）或A->a|Ba（左线性）。

由此便可得出四类文法的关系：见下图

文法的二义性：对于某文法的同一个句子存在两种不同的语法树。如下图：

由语法树我们得出句子“i+i*i”是二义性的。
既然文法会出现二义性，那么怎么解决二义性呢？办法有二：修改编译算法；修改文法。
1.直接左递归的消除

消除产生式中的直接左递归是比较容易的。例如假设非终结符P的规则为

P→Pα / β

其中，β是不以P开头的符号串。那么，我们可以把P的规则改写为如下的非直接左递归形式： P→βP’

                      P’→αP’ / ε

这两条规则和原来的规则是等价的，即两种形式从P推出的符号串是相同的。
2.间接左递归的消除

直接左递归见诸于表面，利用以上的方法可以很容易将其消除，即把直接左递归改写成直接右递归。然而文法表面上不存在左递归并不意味着该文法就不存在左递归了。有些文法虽然表面上不存在左递归，但却隐藏着左递归。例如，设有文法G[S]：

S→Qc/ c

Q→Rb/ b

R→Sa/ a

虽不具有左递归，但S、Q、R都是左递归的，因为经过若干次推导有

SQcRbcSabc

QRbSabQcab

RSaQcaRbca

就显现出其左递归性了，这就是间接左递归文法。

消除间接左递归的方法是，把间接左递归文法改写为直接左递归文法，然后用消除直接左递归的方法改写文法。

如果一个文法不含有回路，即形如PP的推导，也不含有以ε为右部的产生式，那么就可以采用下述算法消除文法的所有左递归。