数据结构(12)--二叉树的静态链表存储和遍历的实现
参考书籍:数据结构(C语言版)严蔚敏吴伟民编著清华大学出版社
本文中的代码可从这里下载:https://github.com/qingyujean/data-structure
1.二叉树的定义
二叉树(Binary Tree)是结点的有限集合,这个集合或者是空,或者是由一个根结点和两棵互不相交的称为左子树和右子树的二叉树构成。
以上对二叉树的定义也是一种递归的方式,二叉树也是树,它是一种特殊的树,每一个结点最多只能有两棵子树,而且它的子树也满足二叉树的定义,也是或者为空,或者是一个根结点和两个称为左子树和右子树的二叉树构成。
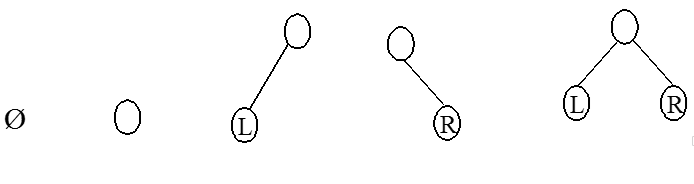
二叉树的特点是每个结点最多有两个孩子,或者说,在二叉树中,不存在度大于2的结点,并且二叉树是有序树(树为无序树),其子树的顺序不能颠倒,因此,二叉树有五种不同的形态,参见下图:
二叉树的性质:
1.二叉树第i层上最多有2i-1个结点(i≥1)。
2.深度为k的二叉树最多有2k-1个结点(k≥1)。
3.在任意二叉树中,叶子结点的数目(即度为0的结点数)等于度为2的结点数加1。即n0=n2+1。
4.具有n个结点的完全二叉树高度为log2(n)向下取整+1 或 log2(n+1)向上取整 。
5.如果将一棵有n个结点的完全二叉树从上到下,从左到右对结点编号1,2,…,n,然后按此编号将该二叉树中各结点顺序地存放于一个一维数组中,并简称编号为j的结点为 j(1≤j≤n),则有如下结论成立:
(1)若 j=1,则结点j为根结点,无双亲,否则j的双亲为 (j/2)向下取整;
(2)若2j≤n,则结点j的左子女为2j ,否则无左子女。即满足 2j>n的结点为叶子结点;
(3)若2j+1≤n,则结点j的右子女为2j+1,否则无右子女;
(4)若结点j序号为奇数且不等于1,则它的左兄弟为j-1;
(5)若结点j序号为偶数且不等于n,它的右兄弟为j+1;
(6) 结点j所在层数(层次)为(log2j)向下取整+1;
补充:
6.有n个节点的完全二叉树有(n/2)向上取整个叶子节点。
7.给定一个前序序列和一个中序序列,或者给定一个中序序列和后序序列,可以唯一确定一个二叉树。
2.二叉树的存储
2.1顺序存储结构
#define MAX_TREE_SIZE 50
typedef char TElemType;
typedef TElemType SqBiTree[MAX_TREE_SIZE];
SqBiTree tree;对于节点tree[i],双亲结点:tree[i/2]
左孩子结点:tree[2*i]
右孩子结点:tree[2*i+1]
对于一般的二叉树,在二叉树中补上若干虚拟结点使其成为完全二叉树,然后,按上述方法存储。 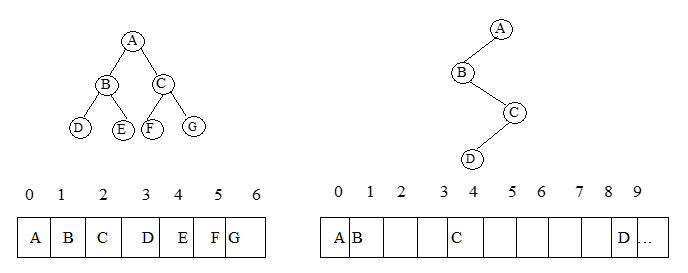
对于一棵二叉树,若采用顺序存贮时,当它为完全二叉树时,比较方便,若为非完全二叉树,将会浪费大量存贮存贮单元。最坏的非完全二叉树是全部只有右分支,设高度为K,则需占用2k-1个存储单元,而实际只有k个元素,实际只需k个存储单元。因此,对于非完全二叉树,宜采用下面的链式存储结构。
2.2链式存储结构
2.2.1动态二叉链表
typedef char TElemType;
//动态二叉链表
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
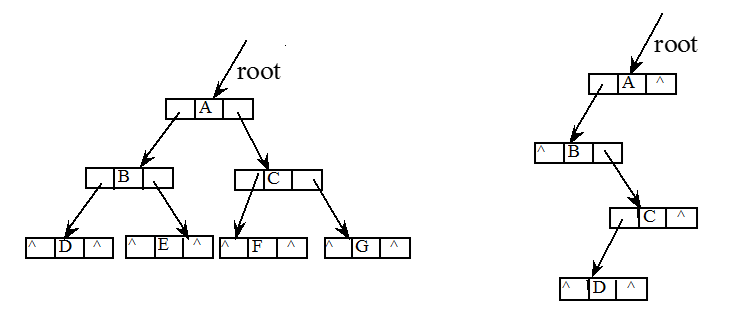
对于一棵二叉树,若采用二叉链表存储时,当二叉树为非完全二叉树时,比较方便,若为完全二叉树时,将会占用较多存储单元(存放地址的指针)。
若一棵二叉树有n个结点,采用二叉链表作存储结构时,共有2n个指针域,其中只有n-1个指针指向左右孩子,其余n+1个指针为空,没有发挥作用,被白白浪费掉了,但我们可以利用这些空链域存储其他有用信息,从而得到另一种链式存储结构----线索链表,将在以后的博文中逐渐介绍。
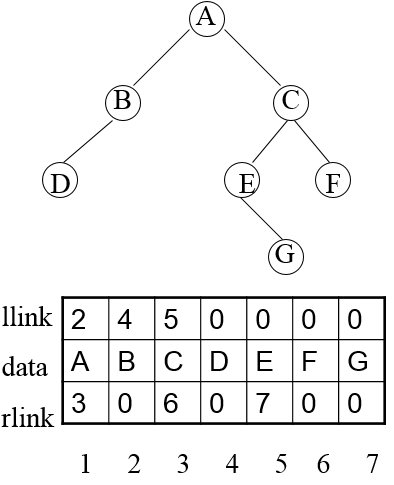
2.2.2静态二叉链表
#define MAXSIZE 20
typedef char TElemType;
typedef struct{
int llink;
TElemType data;
int rlink;
}BiNode;
typedef BiNode BiTree[MAXSIZE+1];//下标为0的单元空出来
3.二叉树的静态链表存储以及遍历的实现
遍历:系统地访问数据结构中的结点, 每个结点都正好被访问一次。
遍历二叉树的过程实际上就是把二叉树中的结点形成一个线性序列的过程,或者说把二叉树线性化。
层次遍历、前序遍历、中序遍历、后序遍历
测试实例:
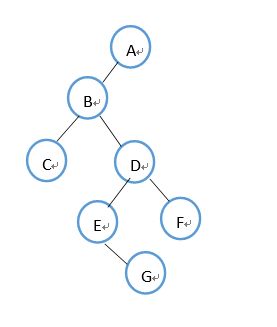
测试按先序序列输入:abc..de.g..f...#,点号代表空树,#为输入结束符
3.1定义静态二叉链表
#include
#define MAXSIZE 20
typedef char TElemType;
typedef struct{
int llink;
TElemType data;
int rlink;
}BiNode;
typedef BiNode BiTree[MAXSIZE+1];//下标为0的单元空出来 3.2按先序序列输入创建二叉树的递归算法
//按先序次序输入二叉树中结点的值(一个字符),点号字符表示空树,构造二叉链表表示的二叉树T
void createBiTree(BiTree &T, int &root, int &i){
TElemType e;
scanf("%c", &e);
if(e!='#'){
if(e!='.'){//输入的当前节点不是“空树”,是实结点
T[i].data = e;
//T[i].llink = 0;
//T[i].rlink = 0;
root = i;
createBiTree(T, T[root].llink, ++i);
createBiTree(T, T[root].rlink, ++i);
}else{
root = 0;//输入的当前节点是“空树”,是虚结点,则对应指向它的链为0
i--;//静态链表下标回退,因为空树没有进表,只有实节点进表了
}
}
}
3.3先序遍历二叉树的递归算法
//先序遍历二叉树(根、左、右)(递归算法)
void preOrderPrint(BiTree T, int root){
if(root){//根节点不为空
printf("%c ", T[root].data);
preOrderPrint(T, T[root].llink);
preOrderPrint(T, T[root].rlink);
}
}3.4先序遍历二叉树的非递归算法
//先序遍历二叉树(根、左、右)(非递归算法)
void preOrderPrint2(BiTree T, int root){
//BiNode s[MAXSIZE];//维护一个栈,用来记录遍历的节点
int s[MAXSIZE];//维护一个栈,用来记录遍历的节点
int top = 0;//指向栈顶元素的下一个位置,初始时top = 0
int pointer = root;//pointer指向当前层的根节点
while(pointer || top){
if(pointer){//根节点不为空
printf("%c ", T[pointer].data);
//s[top++] = T[pointer];//根节点入栈
s[top++] = pointer;//根节点入栈
pointer = T[pointer].llink;//找根节点的左孩子
}else{//根节点为空
//BiNode topElem = s[--top];//栈顶元素出栈,即上一层的根节点
//pointer = topElem.rlink;
int topElemPt = s[--top];//栈顶元素出栈,即上一层的根节点
pointer = T[topElemPt].rlink;
}
}
}演示:
void main(){
BiTree tree;
int root = 1;//根节点的位置
printf("请按先序次序输入二叉树各节点以#号结束,空树用点号代替:\n");
int pos = 1;//控制加入静态数组的位置
createBiTree(tree, root, pos);
printf("先序遍历打印二叉树(递归算法):\n");
preOrderPrint(tree, root);
printf("\n");
printf("先序遍历打印二叉树(非递归算法):\n");
preOrderPrint2(tree, root);
printf("\n");
}
3.5中序遍历二叉树的递归算法
//中序遍历二叉树(左、根、右)(递归算法)
void inOrderPrint(BiTree T, int root){
if(root){//根节点不为空
inOrderPrint(T, T[root].llink);
printf("%c ", T[root].data);
inOrderPrint(T, T[root].rlink);
}
}3.6中序遍历二叉树的非递归算法
//中序遍历二叉树(左、根、右)(非递归算法)
void inOrderPrint2(BiTree T, int root){
//BiNode s[MAXSIZE];//维护一个栈,用来记录遍历的节点
int s[MAXSIZE];//维护一个栈,用来记录遍历的节点
int top = 0;//指向栈顶元素的下一个位置,初始时top = 0
int pointer = root;//pointer指向当前层的根节点
while(pointer || top){
if(pointer){//根节点不为空
//s[top++] = T[pointer];//根节点入栈
s[top++] = pointer;//根节点入栈
pointer = T[pointer].llink;//找根节点的左孩子
}else{//根节点为空
//BiNode topElem = s[--top];//栈顶元素出栈,即上一层的根节点
//printf("%c ", topElem.data);
//pointer = topElem.rlink;
int topElemPt = s[--top];//栈顶元素出栈,即上一层的根节点
printf("%c ", T[topElemPt].data);
pointer = T[topElemPt].rlink;
}
}
}演示:
void main(){
BiTree tree;
int root = 1;//根节点的位置
printf("请按先序次序输入二叉树各节点以#号结束,空树用点号代替:\n");
int pos = 1;//控制加入静态数组的位置
createBiTree(tree, root, pos);
printf("中序遍历打印二叉树(递归算法):\n");
inOrderPrint(tree, root);
printf("\n");
printf("中序遍历打印二叉树(非递归算法):\n");
inOrderPrint2(tree, root);
printf("\n");
}
3.7后序遍历二叉树的递归算法
//后序遍历二叉树(左、右、根)(递归算法)
void postOrderPrint(BiTree T, int root){
if(root){//根节点不为空
postOrderPrint(T, T[root].llink);
postOrderPrint(T, T[root].rlink);
printf("%c ", T[root].data);
}
}3.8后序遍历二叉树的非递归算法
//后序遍历二叉树(左、右、根)(非递归算法)
void postOrderPrint2(BiTree T, int root){
//BiNode s[MAXSIZE];//维护一个栈,用来记录遍历的节点
int s[MAXSIZE];//维护一个栈,用来记录遍历的节点指针
int top = 0;//指向栈顶元素的下一个位置,初始时top = 0
int pointer = root;//pointer指向当前层的根节点
while(pointer || top){
if(pointer){//根节点不为空
//s[top++] = T[pointer];//根节点入栈
s[top++] = pointer;//根节点指针入栈
pointer = T[pointer].llink;//找根节点的左孩子
}else{//根节点为空
//BiNode topElem = s[top-1];//取得栈顶元素,即上一层的根节点
int topElemPt = s[top-1];//取得栈顶元素指针,即上一层的根节点指针
if(topElemPt > 0){//当前层根节点的右子树还没有被访问过,则访问右子树,并赋“右子树已遍历”标志
pointer = T[topElemPt].rlink;
s[top-1] = -s[top-1];
}else{
//BiNode topElem = s[--top];//栈顶元素出栈,即上一层的根节点
topElemPt = -topElemPt;//还原
printf("%c ", T[topElemPt].data);
top--;
}
}
}
}演示:
void main(){
BiTree tree;
int root = 1;//根节点的位置
printf("请按先序次序输入二叉树各节点以#号结束,空树用点号代替:\n");
int pos = 1;//控制加入静态数组的位置
createBiTree(tree, root, pos);
printf("后序遍历打印二叉树(递归算法):\n");
postOrderPrint(tree, root);
printf("\n");
printf("后序遍历打印二叉树(非递归算法):\n");
postOrderPrint2(tree, root);
printf("\n");
}
3.9按层次遍历二叉树的非递归算法
typedef BiNode QElemType;
typedef struct{
//QElemType data[20];
QElemType data[20];
int f;//指向队头元素
int r;//指向对尾元素的下一个位置
}SqQueue;
//初始化一个空队列
void initQueue(SqQueue &Q){
Q.f = Q.r = 0;
}
//按层次遍历二叉树(从上到下、从左到右)
void hierarchicalTraversePrint(BiTree T, int root){
SqQueue Q;//维护一个队列,按层次从上到下、从左到右存放二叉树的各个节点(实际上是按广度优先搜索算法实现层次遍历)
initQueue(Q);
//BiNode queue[20];
//根节点入队
Q.data[Q.r] = T[root];
Q.r++;
while(Q.f != Q.r){
//先降队头元素的左孩子(实节点)入队
if(Q.data[Q.f].llink){
Q.data[Q.r] = T[Q.data[Q.f].llink];
Q.r++;
}
//将队头元素的右孩子(实节点)入队
if(Q.data[Q.f].rlink){
Q.data[Q.r] = T[Q.data[Q.f].rlink];
Q.r++;
}
//打印(访问)队头元素,并将其出队
printf("%c ", Q.data[Q.f].data);
Q.f++;
}演示:
void main(){
BiTree tree;
int root = 1;//根节点的位置
printf("请按先序次序输入二叉树各节点以#号结束,空树用点号代替:\n");
int pos = 1;//控制加入静态数组的位置
createBiTree(tree, root, pos);
printf("按层次遍历打印二叉树(非递归算法):\n");
hierarchicalTraversePrint(tree, root);
printf("\n");
}
4.遍历二叉树的应用
4.1求二叉树的深度
//求二叉树的深度
int getBiTreeDepth(BiTree T, int root){
if(!root)//根节点为空树
return 0;
int leftTreeDepth = getBiTreeDepth(T, T[root].llink);
int rightTreeDepth = getBiTreeDepth(T, T[root].rlink);
return leftTreeDepth > rightTreeDepth ? (leftTreeDepth + 1) : (rightTreeDepth + 1);
}
演示:
void main(){
BiTree tree;
int root = 1;//根节点的位置
printf("请按先序次序输入二叉树各节点以#号结束,空树用点号代替:\n");
int pos = 1;//控制加入静态数组的位置
createBiTree(tree, root, pos);
int depth = getBiTreeDepth(tree, root);
printf("该二叉树的深度为:%d\n", depth);
}
4.2求二叉树的结点数
//求二叉树的结点数
int getBiTreeSize(BiTree T, int root){
if(!root)
return 0;
int leftTreeSize = getBiTreeSize(T, T[root].llink);
int rightTreeSize = getBiTreeSize(T, T[root].rlink);
return leftTreeSize + rightTreeSize + 1;
}演示:
void main(){
BiTree tree;
int root = 1;//根节点的位置
printf("请按先序次序输入二叉树各节点以#号结束,空树用点号代替:\n");
int pos = 1;//控制加入静态数组的位置
createBiTree(tree, root, pos);
int size = getBiTreeSize(tree, root);
printf("该二叉树的结点数为:%d\n", size);
}
4.3求二叉树的叶子节点数
//先序遍历的方法求二叉树的叶子节点数
int getBiTreeLeafNodesNum(BiTree T, int root){
if(!root)
return 0;
else{//根节点不为空树
if(!T[root].llink && !T[root].rlink){//如果当前根节点的左右孩子均不为空
return 1;
}
int leftTreeLeafNodesNum = getBiTreeLeafNodesNum(T, T[root].llink);
int rightTreeLeafNodesNum = getBiTreeLeafNodesNum(T, T[root].rlink);
return leftTreeLeafNodesNum + rightTreeLeafNodesNum;
}
}演示:
void main(){
BiTree tree;
int root = 1;//根节点的位置
printf("请按先序次序输入二叉树各节点以#号结束,空树用点号代替:\n");
int pos = 1;//控制加入静态数组的位置
createBiTree(tree, root, pos);
int leafNodesNum = getBiTreeLeafNodesNum(tree, root);
printf("该二叉树的叶子结点数为:%d\n", leafNodesNum);
}