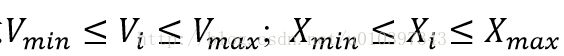从遗传算法、粒子群算法、模拟退火算法理解启发式算法优化的本质
温馨小提示:本文章主要提炼了遗传算法(GA)、粒子群算法(PSO)和模拟退火算法(SA)的精髓,故更适合具有一定基础的童鞋加深理解。
1.1 遗传算法(GA)
1.1.1 实际问题中
(1)确定目标函数,并建立与遗传算法中适应度函数的关系
(2)确定需要优化的参数
1.1.2 遗传算法的寻优过程
(1)根据之前确定的优化参数进行编码;
(2)确定种群规模,并对种群进行初始化;
(3)选择其中一部分个体或全部个体,按照预定的交叉概率进行交叉操作;
(4)选择其中一部分个体或全部个体,按照预定的变异概率进行变异操作;
(5)根据适应度函数以及相应的新解接受准则进行子代的选择;
(6)终止准则。
1.2 模拟退火算法(SA)
1.2.1 概念
模拟退火算法的简单理解:加热到较高温度缓慢冷却到结晶的过程中,类似热力学系统,随着温度的缓慢降低,系统能量逐渐趋于最低的过程。
1.2.2 核心部分
模拟退火算法包含内外两重循环:其中外循环由温度控制,而温度受初始温度、终止温度和温度衰减因子决定,温度对Metropolis准则具有影响;内循环由自己设定的次数确定,主要是控制每个温度下新解的产生次数,与缓慢降温过程相对应。
Metropolis准则:
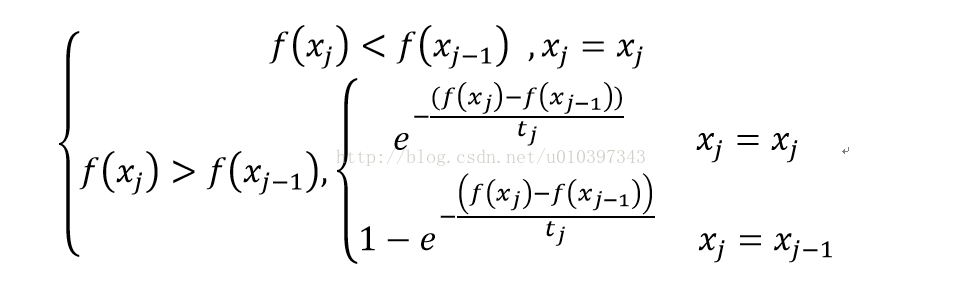
上式中,![]() 表示目标函数,
表示目标函数, 分别表示最新解和上一次得到的解,
分别表示最新解和上一次得到的解, 表示当前的温度,由Metropolis法则可以看出:温度较高时,接受较差解的概率比较大,而温度较低时,接受较差解的概率比较小。和一般搜索算法的思想类似:前期搜索过程增大搜索空间,避免陷入局部最优;后期搜索过程减小搜索空间,使近似最优解更逼近全局最优解【大范围的粗略搜索+局部的精细搜索】。
表示当前的温度,由Metropolis法则可以看出:温度较高时,接受较差解的概率比较大,而温度较低时,接受较差解的概率比较小。和一般搜索算法的思想类似:前期搜索过程增大搜索空间,避免陷入局部最优;后期搜索过程减小搜索空间,使近似最优解更逼近全局最优解【大范围的粗略搜索+局部的精细搜索】。
模拟退火算法具有全局收敛的条件:
(1)初始温度足够高、终止温度足够低:保证足够迭代次数,且控制Metropolis准则;
(2)降温过程足够缓慢:内循环保证足够的次数,新解产生具有足够多的次数。
1.3 粒子群算法(PSO)
1.3.1 概念
粒子群算法(PSO):模仿鸟类觅食行为,结合自身经验和他人信息产生新解。
粒子有两个属性:速度+位置。
1.3.2 核心部分
上式中, 
![]() 表示第i个粒子第k+1次迭代得到的速度,
表示第i个粒子第k+1次迭代得到的速度,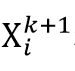 表示第i个粒子第k+1次迭代得到的位置。
表示第i个粒子第k+1次迭代得到的位置。
w表示的是惯性因子,值在0-1之间,可以设置为随迭代次数减小的值,类似变步长搜索方法,可以实现【大范围的粗略搜索+局部的精细搜索】。
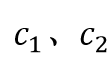 分别表示加速常数,是一个非负数。
分别表示加速常数,是一个非负数。 是随机数,体现了新解产生的随机性。
是随机数,体现了新解产生的随机性。
 表示第i个粒子历代产生的最优解,
表示第i个粒子历代产生的最优解, 表示所有粒子历代产生的最优解。
表示所有粒子历代产生的最优解。
1.4启发式算法总结
1.4.1 三种启发式算法的共同点
首先解释下启发式算法:Heuristics Algorithm,和网上某些博主的观点相同,感觉翻译为试探法更为合适。
相对于梯度下降法等类似方法而言,试探法体现了随机性;
相对于盲目搜索算法而言,试探法又具有一定的方向性。
1.4.2 启发式算法的5大基本要素
试探法有5大基本要素:
(1)随机初始化可行解;
(2)评价函数或目标函数的确定;
(3)新解的产生机制;
(4)新解的接受机制;
(5)终止准则。
1.4.3 启发式算法的本质
试探法的本质是并行、随机、有一定方向的搜索方法。为了便于理解,以遗传算法、模拟退火算法和粒子群算法对试探法的本质进行进一步解释。
并行性的体现:遗传算法中每代种群具备一定数量;模拟退火算法中内循环的体现(要求降温过程足够缓慢);粒子群算法中粒子的数量。
随机性的体现:遗传算法中新解的产生机制(交叉和变异)、新解的接受机制(轮盘赌);模拟退火算法中新解的产生机制、新解的接受机制(Metropolis准则);粒子群算法中新解的产生机制(自身经验和他人信息前面的随机系数r1和r2)。
方向性的体现(逐渐向最优解逼近):遗传算法中新解的接受机制(精英保留策略、轮盘赌);模拟退火算法中新解的接受机制(Metropolis准则:绝对接受更优解,以一定概率接受较差的解,且随着温度的降低,接受较差解的概率降低,即开始降温过程搜索空间大,增强全局收敛能力,接近稳定状态,更不易接受较差解,使局部搜索更为精确);粒子群算法中新解的产生机制(新解的产生来自于粒子本身最优解和所有粒子最优解的引导)。
综合试探法的要素和本质可以看出,试探法中新解的产生机制和接受机制对于算法的全局收敛能力十分重要,有助于克服局部最优问题。
1.4.4 启发式算法的不足
虽然人们研究对启发式算法的研究将近50年,但它还有很多不足:
(1)启发式算法目前缺乏统一、完整的理论体系;
(2)由于NP理论,各种启发式算法都不可避免的遭遇到局部最优的问题,如何判断;
(3)各种启发式算法都有个自优点如何,完美结合;
(4)启发式算法中的参数对算法的效果起着至关重要的作用,如何有效设置参数;
(5)启发算法缺乏有效的迭代停止条件;
(6)启发式算法收敛速度的研究等。