论文阅读笔记:SENet: Squeeze-and-Excitation Networks
论文阅读笔记:SENet: Squeeze-and-Excitation Networks
本文主要包含如下内容:
论文地址
代码地址
参考博客
- 论文阅读笔记:SENet: Squeeze-and-Excitation Networks
- 主要思想
- 网络结构
- 实验结果
- 代码实现
本篇论文主要聚焦于通道维度,并提出一种新的结构单元——“Squeeze-and-Excitation(SE)”单元,对通道间的依赖关系进行建模,可以自适应的调整各通道的特征响应值。只增加很小的计算消耗,但却可以极大地提升网络性能.获得ILSVRC2017分类任务的第一名,top-5错误率为2.251%。
主要思想
传统的卷积核作为卷积神经网络的核心,通常被看做是在局部感受野上,将空间上(spatial)的信息和特征维度上(channel-wise)的信息进行聚合的信息聚合体。卷积神经网络由一系列卷积层、非线性层和下采样层构成,这样它们能够从全局感受野上去捕获图像的特征来进行图像的描述。但是并没有考虑卷积滤波器之间的相关性,即通道相关性.本文提出一种新的网络单元——“Squeeze-and-Excitation(SE)” block,希望通过对各通道的依赖性进行建模以提高网络的表示能力,并且可以对特征进行逐通道调整,这样网络就可以学习通过全局信息来有选择性的加强包含有用信息的特征并抑制无用特征。
网络结构
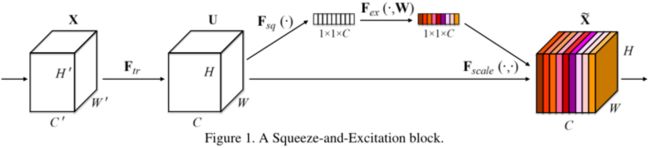
第一步squeeze操作,顺着空间维度来进行特征压缩,将每个二维的特征通道变成一个实数,这个实数某种程度上具有全局的感受野,并且输出的维度和输入的特征通道数相匹配。压缩(squeeze)全局空间信息形成一个通道描述符,这里使用全局平均池化来生成各通道的统计量。
第二步excitation操作,学习对各通道的依赖程度,并根据依赖程度的不同对特征图进行调整,调整后的特征图就是SE block的输出。为了实现多个通道都能够影响结果,本文使用sigmoid激活函数的门限机制来实现(而不使用softmax函数:对应单一函数).为了限制模型复杂度并增强泛化能力,门限机制中使用bottleneck形式的两个全连接层,第一个FC层降维至1/r,r为超参数,本文取16.
在excitation操作中,首先将特征维度降低到输入的 1/16,然后经过 ReLu 激活后再通过一个 Fully Connected 层升回到原来的维度。这样做比直接用一个 Fully Connected 层的好处在于:1)具有更多的非线性,可以更好地拟合通道间复杂的相关性;2)极大地减少了参数量和计算量。
由于squeeze操作,即使用了全局信息,因此SENet可以放在低层和高层特征表达中,增加低层的特征表达,增加高层的类别相关性.
在Inception网络和ResNet网络中加入SE block:

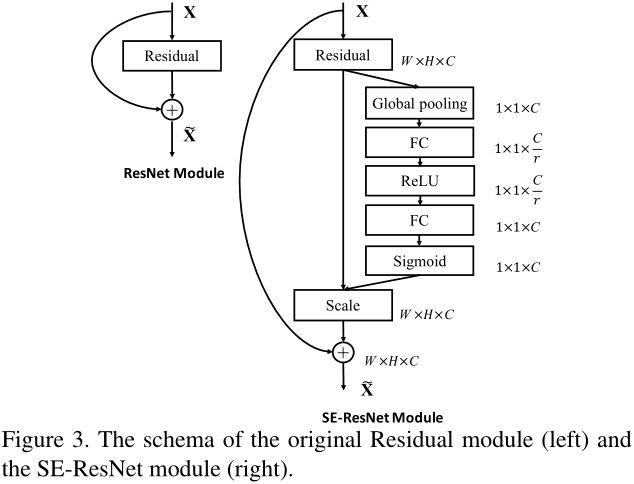
实验结果
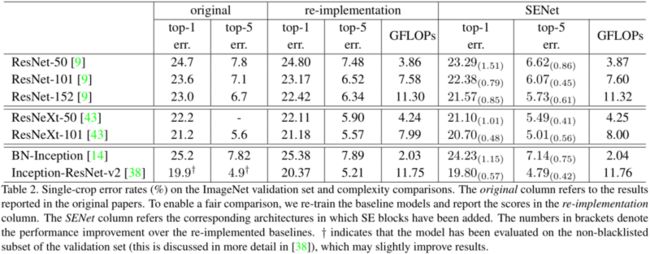
实验结果表明:SE block根据输入动态调整各通道的特征,增强网络的表示能力。另外也可以用于辅助网络修剪/压缩的工作。
代码实现
这里使用了caffe中的Scale层,这里简要分析 Caffe proto中ScaleParameter / scale_layer.hpp/ scale_layer.cpp
下面是Caffe proto中ScaleParameter,一共有四个参数组成,详情如下:
message ScaleParameter {
// The first axis of bottom[0] (the first input Blob) along which to apply
// bottom[1] (the second input Blob). May be negative to index from the end
// (e.g., -1 for the last axis).
//
// For example, if bottom[0] is 4D with shape 100x3x40x60, the output
// top[0] will have the same shape, and bottom[1] may have any of the
// following shapes (for the given value of axis):
// (axis == 0 == -4) 100; 100x3; 100x3x40; 100x3x40x60 // axis == 0的形状
// (axis == 1 == -3) 3; 3x40; 3x40x60 // axis == 1的形状
// (axis == 2 == -2) 40; 40x60 // axis == 2的形状
// (axis == 3 == -1) 60 // axis == 3的形状
// Furthermore, bottom[1] may have the empty shape (regardless of the value of
// "axis") -- a scalar multiplier.
optional int32 axis = 1 [default = 1]; // 处理维度,即从哪个通道数开始处理
// (num_axes is ignored unless just one bottom is given and the scale is
// a learned parameter of the layer. Otherwise, num_axes is determined by the
// number of axes by the second bottom.)
// The number of axes of the input (bottom[0]) covered by the scale
// parameter, or -1 to cover all axes of bottom[0] starting from `axis`.
// Set num_axes := 0, to multiply with a zero-axis Blob: a scalar.
optional int32 num_axes = 2 [default = 1]; // 忽略,由即 bottom[1] 形状决定,如果不存在第二个 bottom,则需要制定标量还是矢量相乘,即确定总共处理的通道维度
// (filler is ignored unless just one bottom is given and the scale is
// a learned parameter of the layer.)
// The initialization for the learned scale parameter.
// Default is the unit (1) initialization, resulting in the ScaleLayer
// initially performing the identity operation.
optional FillerParameter filler = 3; // 忽略,如果不存在第二个 bottom,则说明该参数需要学习,需要初始化 Scale 参数
// Whether to also learn a bias (equivalent to a ScaleLayer+BiasLayer, but
// may be more efficient). Initialized with bias_filler (defaults to 0).
optional bool bias_term = 4 [default = false];
optional FillerParameter bias_filler = 5; // 决定是否学习bias,如果不学习,则可以简化为alpha*x = y
}scale_layer.hpp与其他include文件大同小异,这里,我们只参考引入的参数.具体参数在scale_layer.cpp中讲解
shared_ptr > bias_layer_;
vector sum_multiplier_;
Blob sum_result_;
Blob temp_;
int axis_;
int outer_dim_, scale_dim_, inner_dim_; scale_layer.cpp讲解如下:主要包含了LayerSetup,Reshape ,Forward和Backward
#include ::LayerSetUp(const vector(scale_shape));
FillerParameter filler_param(param.filler()); // 初始化参数
if (!param.has_filler()) { // 如果初始化参数为空,则填写constant
// Default to unit (1) filler for identity operation.
filler_param.set_type("constant");
filler_param.set_value(1);
}
shared_ptr > filler(GetFiller(filler_param)); // 初始化
filler->Fill(this->blobs_[0].get());
}
if (param.bias_term()) { // 处理bias,如果没有bias,则不执行,这里不详细解读
LayerParameter layer_param(this->layer_param_);
layer_param.set_type("Bias");
BiasParameter* bias_param = layer_param.mutable_bias_param();
bias_param->set_axis(param.axis());
if (bottom.size() > 1) {
bias_param->set_num_axes(bottom[1]->num_axes());
} else {
bias_param->set_num_axes(param.num_axes());
}
bias_param->mutable_filler()->CopyFrom(param.bias_filler());
bias_layer_ = LayerRegistry::CreateLayer(layer_param);
bias_bottom_vec_.resize(1);
bias_bottom_vec_[0] = bottom[0];
bias_layer_->SetUp(bias_bottom_vec_, top);
if (this->blobs_.size() + bottom.size() < 3) {
// case: blobs.size == 1 && bottom.size == 1
// or blobs.size == 0 && bottom.size == 2
bias_param_id_ = this->blobs_.size();
this->blobs_.resize(bias_param_id_ + 1);
this->blobs_[bias_param_id_] = bias_layer_->blobs()[0];
} else {
// bias param already initialized
bias_param_id_ = this->blobs_.size() - 1;
bias_layer_->blobs()[0] = this->blobs_[bias_param_id_];
}
bias_propagate_down_.resize(1, false);
}
this->param_propagate_down_.resize(this->blobs_.size(), true);
}
template <typename Dtype>
void ScaleLayer::Reshape(const vector* scale = (bottom.size() > 1) ? bottom[1] : this->blobs_[0].get();
// Always set axis_ == 0 in special case where scale is a scalar
// (num_axes == 0). Mathematically equivalent for any choice of axis_, so the
// actual setting can be safely ignored; and computation is most efficient
// with axis_ == 0 and (therefore) outer_dim_ == 1. (Setting axis_ to
// bottom[0]->num_axes() - 1, giving inner_dim_ == 1, would be equally
// performant.)
axis_ = (scale->num_axes() == 0) ?
0 : bottom[0]->CanonicalAxisIndex(param.axis());
CHECK_GE(bottom[0]->num_axes(), axis_ + scale->num_axes())
<< "scale blob's shape extends past bottom[0]'s shape when applied "
<< "starting with bottom[0] axis = " << axis_;
for (int i = 0; i < scale->num_axes(); ++i) {
CHECK_EQ(bottom[0]->shape(axis_ + i), scale->shape(i))
<< "dimension mismatch between bottom[0]->shape(" << axis_ + i
<< ") and scale->shape(" << i << ")";
}
outer_dim_ = bottom[0]->count(0, axis_); // n
scale_dim_ = scale->count(); // c
inner_dim_ = bottom[0]->count(axis_ + scale->num_axes()); // h*w
if (bottom[0] == top[0]) { // in-place computation
temp_.ReshapeLike(*bottom[0]);
} else {
top[0]->ReshapeLike(*bottom[0]);
}
sum_result_.Reshape(vector<int>(1, outer_dim_ * scale_dim_)); // 保存结果NC_1_1_1
const int sum_mult_size = std::max(outer_dim_, inner_dim_);
sum_multiplier_.Reshape(vector<int>(1, sum_mult_size));
if (sum_multiplier_.cpu_data()[sum_mult_size - 1] != Dtype(1)) {
caffe_set(sum_mult_size, Dtype(1), sum_multiplier_.mutable_cpu_data());
}
if (bias_layer_) {
bias_bottom_vec_[0] = top[0];
bias_layer_->Reshape(bias_bottom_vec_, top);
}
}
template <typename Dtype>
void ScaleLayer::Forward_cpu( // 前向传播,完成乘以alpha与+bias的操作,由于alpha与bias均为C的向量,因此需要先进行广播。
const vector::Backward_cpu(const vector* scale = scale_param ? this->blobs_[0].get() : bottom[1];
if ((!scale_param && propagate_down[1]) ||
(scale_param && this->param_propagate_down_[0])) {
const Dtype* top_diff = top[0]->cpu_diff();
const bool in_place = (bottom[0] == top[0]);
const Dtype* bottom_data = (in_place ? &temp_ : bottom[0])->cpu_data();
// Hack: store big eltwise product in bottom[0] diff, except in the special
// case where this layer itself does the eltwise product, in which case we
// can store it directly in the scale diff, and we're done.
// If we're computing in-place (and not doing eltwise computation), this
// hack doesn't work and we store the product in temp_.
const bool is_eltwise = (bottom[0]->count() == scale->count());
Dtype* product = (is_eltwise ? scale->mutable_cpu_diff() :
(in_place ? temp_.mutable_cpu_data() : bottom[0]->mutable_cpu_diff()));
caffe_mul(top[0]->count(), top_diff, bottom_data, product);
if (!is_eltwise) {
Dtype* sum_result = NULL;
if (inner_dim_ == 1) {
sum_result = product;
} else if (sum_result_.count() == 1) {
const Dtype* sum_mult = sum_multiplier_.cpu_data();
Dtype* scale_diff = scale->mutable_cpu_diff();
if (scale_param) {
Dtype result = caffe_cpu_dot(inner_dim_, product, sum_mult);
*scale_diff += result;
} else {
*scale_diff = caffe_cpu_dot(inner_dim_, product, sum_mult);
}
} else {
const Dtype* sum_mult = sum_multiplier_.cpu_data();
sum_result = (outer_dim_ == 1) ?
scale->mutable_cpu_diff() : sum_result_.mutable_cpu_data();
caffe_cpu_gemv(CblasNoTrans, sum_result_.count(), inner_dim_,
Dtype(1), product, sum_mult, Dtype(0), sum_result);
}
if (outer_dim_ != 1) {
const Dtype* sum_mult = sum_multiplier_.cpu_data();
Dtype* scale_diff = scale->mutable_cpu_diff();
if (scale_dim_ == 1) {
if (scale_param) {
Dtype result = caffe_cpu_dot(outer_dim_, sum_mult, sum_result);
*scale_diff += result;
} else {
*scale_diff = caffe_cpu_dot(outer_dim_, sum_mult, sum_result);
}
} else {
caffe_cpu_gemv(CblasTrans, outer_dim_, scale_dim_,
Dtype(1), sum_result, sum_mult, Dtype(scale_param),
scale_diff);
}
}
}
}
if (propagate_down[0]) {
const Dtype* top_diff = top[0]->cpu_diff();
const Dtype* scale_data = scale->cpu_data();
Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
for (int n = 0; n < outer_dim_; ++n) {
for (int d = 0; d < scale_dim_; ++d) {
const Dtype factor = scale_data[d];
caffe_cpu_scale(inner_dim_, factor, top_diff, bottom_diff);
bottom_diff += inner_dim_;
top_diff += inner_dim_;
}
}
}
}
#ifdef CPU_ONLY
STUB_GPU(ScaleLayer);
#endif
INSTANTIATE_CLASS(ScaleLayer);
REGISTER_LAYER_CLASS(Scale);
} // namespace caffe