Trie树（字典树，前缀树，键树）分析详解

Trie树概述

   Trie树，又称字典树、前缀树、单词查找树、键树，是一种多叉树形结构，是一种哈希树的变种。Trie这个术语来自于retrieval，发音为/tri:/ “tree”，也有人读为/traɪ/ “try”。Trie树典型应用是用于快速检索（最长前缀匹配），统计，排序和保存大量的字符串，所以经常被搜索引擎系统用于文本词频统计，搜索提示等场景。它的优点是最大限度地减少无谓的字符串比较，查询效率比较高。

   Trie树的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

   Trie树有3个基本性质：

 - 根节点不包含字符，除根节点外每一个节点都只包含一个字符
 - 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串
 - 每个节点的所有子节点包含的字符都不相同

Trie树的插入

   上面我们了解了Trie树的性质，现在我们根据Trie树的性质来创建一个Trie树。假设我们现在有b，abc，abd，bcd，abcd，efg，hii 这6个单词，构建出的Trie树如下图所示：

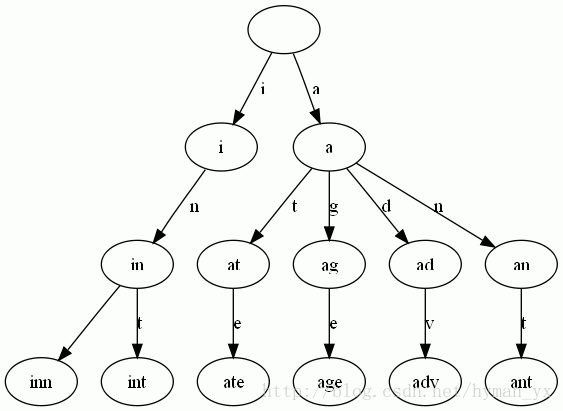
   搭建Trie的方法很简单，其实就是将单词的每个字母逐一插入Trie树。插入前先看字母对应的节点是否存在，存在则共享该节点，不存在则创建对应的节点。比如要插入新单词and，就有下面几步：

 1. 插入第一个字母"a"，发现root节点存在子节点a，则共享节点a
 2. 插入第二个字母"n"，发现节点a存在子节点n，则共享节点n
 3. 插入第三个字母"d"，发现节点n不存在子节点d，则创建子节点d。
 4. 至此，单词and中所有字母已被插入Trie树中，然后设置节点d中的标志位，标记路径root->a->n->d这条路径上所有节点的字符可以组成一个单词and

Trie树的查询

   从root节点开始按照单词的字母顺序向下遍历Trie树，遍历完成有两种情况：

 1. 单词中每个字母都在Trie树中被查找过，此时Trie树不一定被遍历完
 2. 单词中部分字母未在Trie树中被查找过，此时Trie树一定被遍历完

   查询单词是否存在，我们不会管遍历完成时是上面的哪种情况，我们只需要关注遍历结束时Trie树最后一个被遍历的节点last。若节点last中设置了标志位（即表示路径root->…->last上所有节点的字符可以组成一个单词）则表示被查询的单词存在于Trie树中，否则表示不存在。

算法思想

   概述中已经说过，Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

   假设字符的种数有m个，有若干个长度为n的字符串构成了一个Trie树，则每个节点的出度为m（即每个节点的可能子节点数量为m），Trie树的高度为n。很明显我们浪费了大量的空间来存储字符，此时Trie树的最坏空间复杂度为O(m^n)。也正由于每个节点的出度为m，所以我们能够沿着树的一个个分支高效的向下逐个字符的查询，而不是遍历所有的字符串来查询，此时Trie树的最坏时间复杂度为O(n)。这正是空间换时间的体现，也是利用公共前缀降低查询时间开销的体现。

Trie树的实现

Trie树的数组实现原理

Trie树和其它数据结构的比较

Trie树与二叉搜索树

   二叉搜索树应该是我们最早接触的树结构了，我们知道，数据规模为n时，二叉搜索树插入、查找、删除操作的时间复杂度通常只有O(log n)，最坏情况下整棵树所有的节点都只有一个子节点，退变成一个线性表，此时插入、查找、删除操作的时间复杂度是O(n)。

   通常情况下，Trie树的高度n要远大于搜索字符串的长度m，故查找操作的时间复杂度通常为O(m)，最坏情况下的时间复杂度才为O(n)。很容易看出，Trie树最坏情况下的查找也快过二叉搜索树。

   文中Trie树都是拿字符串举例的，其实它本身对key的适宜性是有严格要求的，如果key是浮点数的话，就可能导致整个Trie树巨长无比，节点可读性也非常差，这种情况下是不适宜用Trie树来保存数据的；而二叉搜索树就不存在这个问题。

Trie树与Hash表

   考虑一下Hash冲突的问题。Hash表通常我们说它的复杂度是O(1)，其实严格说起来这是接近完美的Hash表的复杂度，另外还需要考虑到hash函数本身需要遍历搜索字符串，复杂度是O(m)。在不同键被映射到“同一个位置”（考虑closed hashing，这“同一个位置”可以由一个普通链表来取代）的时候，需要进行查找的复杂度取决于这“同一个位置”下节点的数目，因此，在最坏情况下，Hash表也是可以成为一张单向链表的。

   Trie树可以比较方便地按照key的字母序来排序（整棵树先序遍历一次就好了），这跟绝大多数Hash表是不同的（Hash表一般对于不同的key来说是无序的）。

   在较理想的情况下，Hash表可以以O(1)的速度迅速命中目标，如果这张表非常大，需要放到磁盘上的话，Hash表的查找访问在理想情况下只需要一次即可；但是Trie树访问磁盘的数目需要等于节点深度。

   很多时候Trie树比Hash表需要更多的空间，我们考虑这种一个节点存放一个字符的情况的话，在保存一个字符串的时候，没有办法把它保存成一个单独的块。Trie树的节点压缩可以明显缓解这个问题，后面会讲到。

Trie树与后缀树

TODO

Trie树的改进

1. 按位Trie树（Bitwise Trie）：原理上和普通Trie树差不多，只不过普通Trie树存储的最小单位是字符，但是Bitwise Trie存放的是位而已。位数据的存取由CPU指令一次直接实现，对于二进制数据，它理论上要比普通Trie树快。

2. 节点压缩。

   1. 分支压缩：对于稳定的Trie树，基本上都是查找和读取操作，完全可以把一些分支进行压缩。例如，前图中最右侧分支的inn可以直接压缩成一个节点“inn”，而不需要作为一棵常规的子树存在。Radix树就是根据这个原理来解决Trie树过深问题的。

   2. 节点映射表：这种方式也是在Trie树的节点可能已经几乎完全确定的情况下采用的，针对Trie树中节点的每一个状态，如果状态总数重复很多的话，通过一个元素为数字的多维数组（比如Triple Array Trie）来表示，这样存储Trie树本身的空间开销会小一些，虽说引入了一张额外的映射表。

参考

字典树 - 百度百科
Trie - 维基百科
Trie树详解及其应用
Trie树和其它数据结构的比较