似然函数、最大似然与概率函数的关系

概率：在特性环境下，某件事件发生的可能性。概率在抛硬币之前是有意义的，由因推果
似然：在某件事发生的情况下，产生这个结果的可能环境。似然在抛硬币之后才是有意义的，由果推因。
假设概率表示为（公式1）：

$$\mathcal{P}(x\mid \theta )$$

那么相对应的似然表示为（公式2）：
$$\mathcal{L}(\theta \mid x)$$

一般情况下，虽然描述的东西不同，但似然和概率是等价的（公式3）：
$$\mathcal{P}(x\mid \theta )=\mathcal{L}(\theta \mid x)$$

许多文章、书籍将θ模糊地描述为“前置条件”、“满足某分布的情况下”，其实容易让人理解绕弯。这里举一个抛硬币的例子，就能很轻松地理解：
最开始讲概率论的时候，我们会看到如下的表述（公式4）：
$$\{\begin{array}{r}\mathcal{P}(\xi =1)=\frac{1}{2}\\ \mathcal{P}(\xi =0)=\frac{1}{2}\end{array}$$

表示抛一枚硬币，正面朝上的概率是0.5，背面朝上的概率也是0.5。那么这个是结果，它的原因是什么呢？当然是因为这是一枚均匀的硬币（似乎是废话）。而似然就是一个逆推的过程，在抛了1000次硬币，发现有500次是正面朝上，500次是背面朝上，那么它是一枚什么样的硬币（均匀的吗？非均匀的吗？怎么样非均匀的呢？）呢？而常说的最大似然，就是说它是一枚什么样的硬币可能性最大。
于是公式1在抛硬币的表述下是这样（公式5）：
$$\mathcal{P}(x\mid \theta )=\mathcal{P}(x\mid \theta =\text{均匀的硬币})=\{\begin{array}{r}\mathcal{P}(\xi =1\mid \theta =\text{均匀的硬币})=\frac{1}{2}\\ \mathcal{P}(\xi =0\mid \theta =\text{均匀的硬币})=\frac{1}{2}\end{array}$$

其中：
$$\mathcal{P}(x\mid \theta =\text{均匀的硬币})$$

是一个函数，若输入变量$x=1$，表示正面朝上，即在条件“一枚均匀的硬币”下，正面朝上的概率是0.5。
接下来，我们看看似然是如何表述的：
$$\mathcal{L}(\theta \mid x)=\mathcal{L}(\theta \mid x=\text{抛1000次硬币，500次正面朝上，500次背面朝上})$$

或者表述为
$$\mathcal{L}(\theta \mid x)=\mathcal{L}(\theta \mid x=\text{在“}\mathcal{P}(\xi =1)=\frac{1}{2}\text{和}\mathcal{P}(\xi =0)=\frac{1}{2}\text{”的前提下})$$

这$\mathcal{L}$是一个函数，输入变量是$\theta$，得出的结果是一个概率。我们先不展开具体函数构成，我们可以猜想，假设我们输入“$\theta$=均匀的硬币”，那么可以直觉感受，这样得出来的概率值，显然会比“$\theta$=非均匀的硬币”要大一些。这样的结果是基于“抛1000次硬币，500次正面朝上，500次背面朝上”的实验前提下进行的猜测。这也是似然函数，通过结果推因的思想。

下面考虑一个更复杂的情况：
$$\mathcal{P}(x=\text{抛两次硬币都正面朝上}\mid \theta =\text{均匀的硬币})={\left(\frac{1}{2}\right)}^2=\frac{1}{4}$$

我们以这个$x$现象为前提，忘记目前的环境$\theta$，假设$\theta$是未知的，逆推硬币质量的均匀情况：
$$\mathcal{L}(\theta \mid x)=\mathcal{L}(\theta \mid x=\text{抛两次硬币都正面朝上})$$

为了定量描述这个函数，我们为环境变量$\theta$和实验现象$x$赋予意义：
$$\{\begin{array}{r}\theta \cdots \cdots \text{该硬币性质使得抛一次正面朝上的概率；可知反面朝上概率为}1-\theta \\ x\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \text{具体的实验结果。这个结果决定了函数的组成}\end{array}$$

目前看这样定义，$x$显得非常绕口，什么叫函数的组成呢？我们举个例子：
假设$x$定义为：抛2次硬币正面朝上的概率，那么：
$$\mathcal{P}(x\mid \theta =\frac{1}{2})=\theta \cdot \theta ={\theta }^2$$

由公式3我们可知它和似然函数是等价的：
$$\mathcal{P}(x\mid \theta =\frac{1}{2})=\mathcal{L}(\theta =\frac{1}{2}\mid x)={\theta }^2$$

接下来我们进行转化，把x设为已知，θ设为未知数：
$$\mathcal{P}(x=\frac{1}{4}\mid \theta )=\mathcal{L}(\theta \mid x=\frac{1}{4})={\theta }^2$$

这里其实用0.25来表示$x$并不准确，$x$表达的是抛两次硬币这个含义，因此，为了体现“2次”这个2的含义，$x$应该表示为$x={\theta }^2$。我们选取几个$0\sim 1$的$\theta$来代入函数$\mathcal{L}(\theta \mid x=\frac{1}{4})={\theta }^2$有：

函数	似然概率	$x$	$\theta$
$\mathcal{L}(\theta =0.1\mid x=\frac{1}{4})$	$0.01$	两扔硬币实验，正正概率$\frac{1}{4}$	硬币为“扔一次正面朝上概率为0.1的硬币”的概率是0.01
$\mathcal{L}(\theta =0.3\mid x=\frac{1}{4})$	$0.09$	两扔硬币实验，正正概率$\frac{1}{4}$	硬币为“扔一次正面朝上概率为0.3的硬币”的概率是0.09
$\mathcal{L}(\theta =0.5\mid x=\frac{1}{4})$	$0.25$	两扔硬币实验，正正概率$\frac{1}{4}$	硬币为“扔一次正面朝上概率为0.5的硬币”的概率是0.25
$\mathcal{L}(\theta =0.7\mid x=\frac{1}{4})$	$0.49$	两扔硬币实验，正正概率$\frac{1}{4}$	硬币为“扔一次正面朝上概率为0.7的硬币”的概率是0.49
$\mathcal{L}(\theta =1\mid x=\frac{1}{4})$	$1$	两扔硬币实验，正正概率$\frac{1}{4}$	硬币为“扔一次正面朝上概率为1的硬币”的概率是1

这样是不是很奇怪呢？明明抛两次硬币（两扔硬币实验），正面朝上的概率是25%，为何会得出“硬币为‘扔一次正面朝上概率为1’的硬币”可能性最大（概率100%）的结论呢？
其实这样表述是不对的。
如果抛2次硬币正面朝上的概率不为1，那么暗含着假设，抛2次硬币正面不都朝上的概率是存在，也是一种结果，只有基于这样的结果下才能正确得出整个似然函数的结构。而以上的似然函数，并未把25%信息包含进去，而只包含了“扔了2次硬币，2次都正面朝上”的这个信息。基于这个信息，当然得出硬币怎么扔都是正面朝上的概率最大。事实上公式：
$$\mathcal{P}(x\mid \theta )=\mathcal{L}(\theta \mid x)$$

中$\mathcal{P}(x\mid \theta )$表示的不是一个概率，而应该是一个概率函数。就抛硬币而言，概率函数服从伯努利分布，假设正面朝上（$\xi =1$）的概率为$\theta$，那么抛一次硬币有：
$$\mathcal{P}(x\mid \theta )=\{\begin{array}{l}\mathcal{P}(1)=\theta \\ \mathcal{P}(0)=1-\theta \end{array}={\theta }^x(1-\theta {)}^{1-x}$$

抛两次硬币就不好搞了，此时输入参数$x$如何数值化呢？其实所谓抛2次、抛3次，就是2重、3重伯努利实验，抛N次就是N重伯努利实验。此时$x$不代表概率，而是代表正面朝上的次数（例如$n=2,x=1$表示抛了2次硬币，一共有1次硬币朝上）：
$$\mathcal{P}(x,n\mid \theta )=\left(\genfrac{}{}{0ex}{}{n}{x}\right){\theta }^x(1-\theta {)}^{n-x}=\frac{n!}{x!(n-x)!}{\theta }^x(1-\theta {)}^{n-x}$$

所以，按照刚才的例子，真正抛两次硬币（n=2）情况反过来推$\mathcal{L}$应该为：
$$\mathcal{P}(x,2\mid \theta )=\frac{2!}{x!(2-x)!}{\theta }^x(1-\theta {)}^{2-x}=\mathcal{L}(\theta \mid x,2)$$

那么抛2次，2次都朝上就是：
$$\mathcal{L}(\theta \mid 2,2)={\theta }^2$$

那么抛2次，1次朝上：
$$\mathcal{L}(\theta \mid 1,2)=2\theta (1-\theta )$$

那么抛2次，0次朝上：
$$\mathcal{L}(\theta \mid 1,2)=(1-\theta {)}^2$$

此时，涉及多个独立事件的似然函数，必须将每个事件的概率包含在内：
$$\mathcal{L}=\prod _{i=1}^N{p}_i$$

举个例子，假设进行了4次“两抛硬币”实验，每次实验的概率如下：
$$\{\begin{array}{l}{p}_1=\mathcal{P}(2,2\mid \theta )={\theta }^2\\ p_2=\mathcal{P}(1,2\mid \theta )=2\theta (1-\theta )\\ p_3=\mathcal{P}(1,2\mid \theta )=2\theta (1-\theta )\\ p_4=\mathcal{P}(0,2\mid \theta )=(1-\theta {)}^2\end{array}$$

那么其似然函数为：
$$\mathcal{L}=\prod _{i=1}^N{p}_i={\theta }^2\cdot (2\theta (1-\theta ){)}^2\cdot (1-\theta {)}^2=4{\theta }^2(1-\theta {)}^2$$

函数图像为：

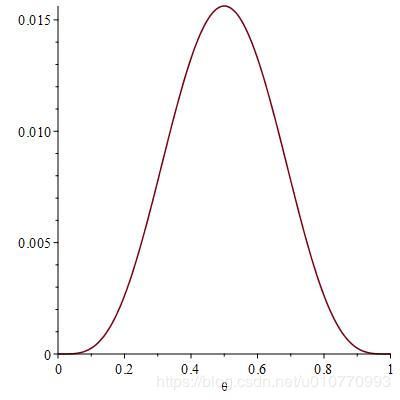
从这个图像，我们就能正确得出硬币是一枚抛一次正面朝上概率是50%（$\theta =0.5$）的概率最大，概率为$\mathcal{L}=1.5625\%$，所以我们就说似然函数L的极值点为(0.5,0.15625)，这就是常说的“最大似然”。这是什么意思呢？意思是，在进行4次两抛硬币实验，结果为1次正正，2次正背，1次背背的情况下，硬币是一个抛一次正面朝上概率为0.5的非均匀硬币的可能性最大。

如果我们进行的试验次数越多，假设抛了100次，25次两抛都朝上，50次对半分，25次两抛都朝下：

$$\mathcal{L}=\prod _{i=1}^{100}{p}_i=1125899906842624\cdot {\theta }^{100}(1-\theta {)}^{100}$$

其函数图像如下：

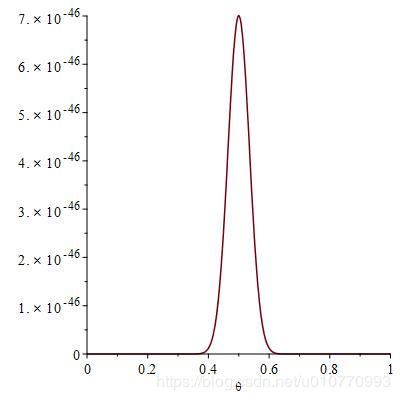
可以发现硬币是一枚均匀硬币的概率远远超过其它情况。所以进行的试验次数越多，通过似然函数极值（最大似然）判断其原本物理属性的准确率就越高。