LeetCode刷题记录(四)
LeetCode刷题记录(四)
1、数组拆分 I
题目:
我的思路:
这一题我的思路分为两步:首先要将这个数组中的元素进行排序,使其成为一个有序数组,然后挑选出其中第奇数个元素,将它们相加的和就是结果。
为什么是第奇数个元素相加呢?根据题目中要求,要选出两两组合中较小的元素相加然后得到最大的总和,所以我们就要使两两组合中较小的那个元素尽量大,因为已经先对这个数组进行了排序,所以这2n个数中值最大的元素就是第2n个数,它是不可能被选出来的,那么比2n小但是比其他的元素都大的数是第2n-1个数,因此它可以被选中,以此类推,我们继续从剩下的2n-2个元素中继续挑选较大的元素,都是奇数索引所对应的元素。
按照这个思路实现的代码如下:
class Solution {
public int arrayPairSum(int[] nums) {
//1、先排序
for (int i = 1; i < nums.length; i++) {
int get = nums[i];
int left = 0;
int right = i - 1;
while (left <= right)
{
int mid = (left + right) / 2;
if (nums[mid] > get)
right = mid - 1;
else
left = mid + 1;
}
for (int j = i - 1; j >= left; j--)
{
nums[j + 1] = nums[j];
}
nums[left] = get;
}
//2、获取第奇数个数相加
int rslt = 0;
for(int a = 0; a < nums.length; a = a + 2) {
rslt += nums[a];
}
return rslt;
}
}
反思:
这一题我是自己写的一个排序方法,可能效率不高,其实可以调用Java提供的数组排序方法。
2、两数之和 II - 输入有序数组
题目:
我的思路:
- 因为这个数组是升序排列的,所以可以定义两个指针i和j分别指向数组的第一个元素和最后一个元素;
- 判断target减去j指向的元素,得到的结果如果小于i指向的元素,那么说明j指向的元素较大,因此j要向前移,如果得到的结果大于i指向的元素,说明i指向的元素较小,i要向后移,这样移动i和j直到得到结果为止。
按照这个思路实现的代码如下:
class Solution {
public int[] twoSum(int[] numbers, int target) {
int i = 0, j = numbers.length - 1;
int[] rslt = new int[2];
while(i < j) {
if(target - numbers[j] < numbers[i]) {
//1、j指向的值较大,j向前移
j--;
} else if(target - numbers[j] > numbers[i]) {
//2、i指向的值较小,i向后移
i++;
} else {
rslt[0] = i + 1;
rslt[1] = j + 1;
break;
}
}
return rslt;
}
}
3、移除元素
题目:
我的思路:
- 因为题目要求要原地移除元素,所以不能定义新的数组,可以定义两个指针i和j分别指向数组第一个元素和最后一个元素;
- 从前向后遍历数组,如果i指向的元素和要移除的元素值相同,那么替换i指向元素的值为j指向的元素,同时j指针向前移动一位,否则直接将i指针向后移动一位;
- 这样移动i和j指针直到两个指针相遇。
按照这个思路实现的代码如下:
class Solution {
public int removeElement(int[] nums, int val) {
if(nums == null || nums.length == 0) {
return 0;
}
if(nums.length == 1 && nums[0] == val) {
return 0;
} else if(nums.length == 1 && nums[0] != val) {
return 1;
}
int i =0, j = nums.length - 1;
while(i <= j) {
if(nums[i] != val) {
i++;
} else {
nums[i] = nums[j];
j--;
}
}
return i;
}
}
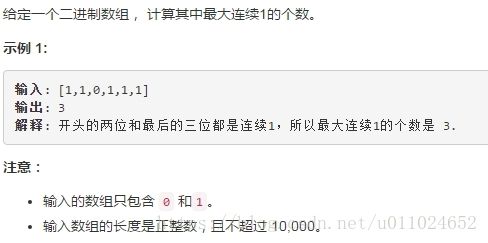
4、最大连续1的个数
题目:
我的思路:
- 这一题也可以定义两个指针i和j,它们属于快慢指针,一开始都是指向的是数组的第一个元素,由j指针依次遍历整个数组;
- 可以判断i指针指向的元素和j指针指向的元素,如果都是1的话,那么可以得到连续1的个数,并且与最大长度进行比较,如果大于最大长度,那么可以得到最新的一个最大长度,如果i和j的值都是0的话,i指针也要向后移动一位,如果j指针为0而i指针为1的话,那么i指针直接指向j指针指向的下一个元素即可。
按照这个思路实现的代码如下:
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int max = 0;
int i = 0, j = 0;
for(; j < nums.length; j++) {
int len = 0;
if(nums[j] == 1 && nums[i] == 1) {
len = j - i + 1;
if(len > max) {
max = len;
}
} else if(nums[j] == 0 && nums[i] == 0) {
i++;
} else if(nums[j] == 0 && nums[i] == 1) {
i = j + 1;
}
}
return max;
}
}
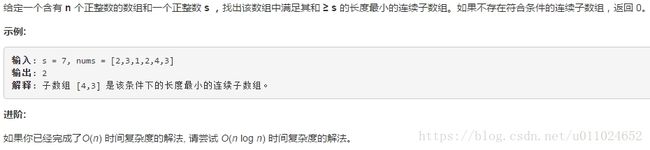
5、长度最小的子数组
题目:
我的思路:
这一题我的思路可能时间复杂度会比较高,仍然定义快慢指针i和j,一开始都是指向数组的第一个元素,由j依次向后遍历,计算i到j值的和,如果和大于等于s,那么向后移动i,再计算i到j值的和,这样依次计算直到最后得到最小长度。
按照这个思路实现的代码如下:
class Solution {
public int minSubArrayLen(int s, int[] nums) {
if(nums == null || nums.length == 0) {
return 0;
}
int rslt = nums.length, sum = 0;
int i = 0, j = 0;
//1、定义一个布尔值用于判断是否得到结果
boolean getRslt = false;
//2、分两种循环,一种是没有得到结果且j遍历到最后,另一种是已经获取到结果并且i还没遍历到最后
while((!getRslt && j <= nums.length - 1) || (getRslt && i < nums.length)) {
for(int m = i; m <= j; m++) {
sum += nums[m];
}
if(sum >= s) {
//3、数字和大于现有的最小值则将最小值赋予rslt,i递增
if(j - i + 1 < rslt) {
rslt = j - i + 1;
}
i++;
getRslt = true;
} else if(j < nums.length){
j++;
//4、如果j遍历到最后了但是已经得到和大于s的情况,则j在最后不变,i递增
//防止{1,2,3} 4死循环
if(j == nums.length && getRslt) {
i++;
j = nums.length - 1;
}
} else if(getRslt && i < nums.length) {
//5、递增i用于跳出循环
i++;
}
sum = 0;
}
if(getRslt) {
return rslt;
} else {
return 0;
}
}
}
反思:
这一题思路比较清晰简单,但是实际编写过程中遇到了一个问题。
一开始我的循环条件没有这么复杂,只是判断j是否遍历到最后了,如果遍历到最后直接跳出循环,这就可能存在一个问题,例如数组为[1, 2, 3],s为4,那么j遍历到最后的时候才得到1+2+3>4,这样直接跳出循环得到的子数组的长度为3,实际上的结果应该是2+3>4长度最小子数组长度为2,j遍历到最后直接跳出循环导致i无法再向后移动。因此我定义了一个布尔值变量用于控制是否得到结果,如果j遍历到最后并且得到了结果,那么j保持不变,i继续向后移动。而跳出循环的条件又分为两个,一个是没有得到最终的结果,但是j已经遍历到最后,另一个是已经得到了最终的结果,i也遍历到最后。
从最终的解法可以看出来,这样做时间复杂度是很高的,特别是对于已经得到结果仍然要等到i遍历到最后的情况,具体优化的方法还在摸索中。
6、旋转数组
题目:
我的思路:
这一题因为也是要求使用原地算法,所以不能定义额外的数组。我设计了一个循环,每次循环也就是向右移动一次数组。如果向右移动一次数组,数组的最后一个值就要移动到数组的第一位,因此可以设置一个临时变量存储数组的最后一个值,等到数组其他位数全部移动完了之后再将原数组最后的一个值设置到新数组的第一位。
按照这个思路实现的代码如下:
class Solution {
public void rotate(int[] nums, int k) {
if(nums == null || nums.length == 0 || nums.length == 1) {
return;
}
//1、对k取模,这是为了防止出现k大于nums长度的情况
//如果k大于nums的长度,那么实际上移动的位置就是k%nums.length位
if(k >= nums.length) {
k = k % nums.length;
}
//2、每次向右移动一次数组,直到移动的步数
for(int i = 0; i < k; i++) {
int lastNum = nums[nums.length - 1];
//3、将第1位到length - 1位向右移动一位
for(int j = nums.length - 2; j >= 0; j--) {
int tmp = nums[j];
nums[j + 1] = tmp;
}
//4、将第0位置为原数组的最后一个数
nums[0] = lastNum;
}
}
}
反思:
这种实现方式因为每次都要移动全部的数组,所以时间复杂度也是比较高的,以后还要继续研究一下是否有更高效的方式。
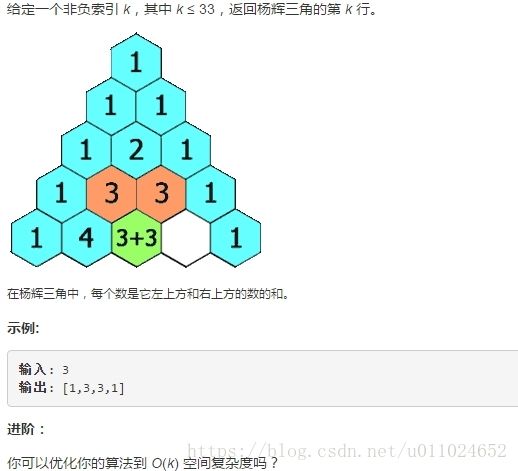
7、杨辉三角 II
题目:
我的思路:
这一题我的思路和第三篇中介绍的《杨辉三角》是一样的,只是最后返回第k行数据即可,题目中进阶要求能否优化算法到O(k)的空间复杂度暂时还未想到好的方式,以后有新的解法可以继续更新。
按照这个思路实现的代码如下:
class Solution {
public List<Integer> getRow(int rowIndex) {
List<List<Integer>> rslt = new ArrayList<List<Integer>>();
List<Integer> row;
for(int i = 0; i <= rowIndex; i++) {
row = new ArrayList<Integer>();
if(i == 0) {
row.add(1);
rslt.add(row);
} else {
for(int j = 0; j <= i; j++) {
if(j - 1 < 0) {
row.add(0 + rslt.get(i - 1).get(j));
} else if(j >= rslt.get(i - 1).size()) {
row.add(rslt.get(i - 1).get(j - 1) + 0);
} else {
row.add(rslt.get(i - 1).get(j - 1) + rslt.get(i - 1).get(j));
}
}
rslt.add(row);
}
}
return rslt.get(rowIndex);
}
}
8、翻转字符串里的单词
题目:
我的思路:
- 先将字符串通过spilt()方法以空格进行分割,得到一个字符串数组;
- 然后使用双指针的方式翻转字符串数组中的单词,在翻转字符串数组中单词的同时要剔除空格;
- 遍历字符串数组拼接一个新的字符串。
按照这个思路实现的代码如下:
public class Solution {
public String reverseWords(String s) {
if(s == null) {
return null;
}
if(s.trim().equals("")) {
return "";
}
//1、先剔除原有字符串中前后多余的空格,然后以空格分割字符串得到字符串数组
String[] words = s.trim().split(" ");
//2、翻转字符串数组
for(int i = 0, j = words.length - 1; i < j;i++, j--) {
String tmp = words[i];
words[i] = words[j].trim();
words[j] = tmp.trim();
}
//3、拼接得到新的字符串
StringBuffer sb = new StringBuffer();
for(int i = 0; i < words.length; i++) {
if(!"".equals(words[i].trim())) {
sb.append(words[i] + " ");
}
}
return sb.toString().trim();
}
}
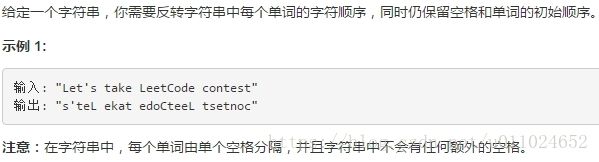
9、反转字符串中的单词 III
题目:
我的思路:
- 首先使用spilt()方法将字符串以空格进行分割,获得字符串数组;
- 将字符串数组中每个字符串进行翻转,先将字符串转换为字符数组,然后使用双指针的方式进行翻转;
- 将翻转后的字符串数组重新拼接成新的字符串。
按照这个思路实现的代码如下:
class Solution {
public String reverseWords(String s) {
if(null == s) {
return null;
}
if("".equals(s.trim())) {
return "";
}
//1、将字符串以空格进行分割
String[] words = s.split(" ");
StringBuffer sb = new StringBuffer();
for(String word : words) {
sb.append(reverseOneWord(word) + " ");
}
return sb.toString().trim();
}
//2、单独写一个方法用于翻转分割后的每个字符串
private String reverseOneWord(String word) {
char[] chars = word.toCharArray();
StringBuffer sb = new StringBuffer();
for(int i = 0, j = chars.length - 1; i < j; i++, j--) {
char tmp = chars[i];
chars[i] = chars[j];
chars[j] = tmp;
}
sb.append(chars);
return sb.toString();
}
}
10、删除排序数组中的重复项
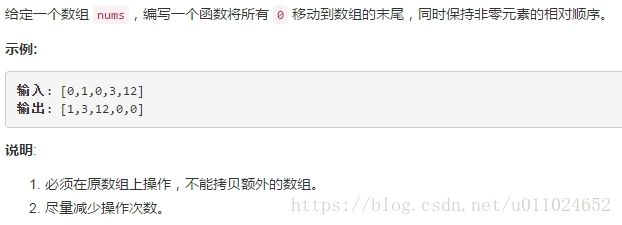
题目:
我的思路:
这一题仍然是要求原地删除数组中的重复项,也就是说仍然不能新定义数组。
我依然使用快慢指针的方式来解决,定义两个指针i和n,i用于从数组第一位开始向后遍历,而n一开始指向i的后一位,即数组第二位。i在遍历数组的时候要判断当前值在数组中是否重复,如果重复了,i向后移一位直到遇到不重复的值为止,然后将第n位的值替换为不重复的值,n向后移动一位,这样循环直到得到最终结果。
按照这个思路实现的代码如下:
class Solution {
public int removeDuplicates(int[] nums) {
if(nums == null || nums.length == 0) {
return 0;
}
if(nums.length == 1) {
return 1;
}
int tmp = nums[0];
int n = 1;
/**
1、使用快慢两个指针,快指针i遍历数组每一个数,并使用一个临时值记录数组的每个重复数字
*/
for(int i = 1; i < nums.length;) {
//2、用m记录i的初始位置
int m = i;
//3、遍历每个数,如果数字重复,i加一
while(i < nums.length && nums[i] == tmp) {
i++;
}
//4、可能遍历到最后,如果遍历到最后则直接退出
if(i >= nums.length) {
break;
}
//5、如果m不等于i,说明出现重复,则将慢指针所指的位置赋值为i所指的数值,即重复数字后一位,如果m等于i,说明未出现重复,i加1即可
if(m != i) {
nums[n] = nums[i];
} else {
i++;
}
tmp = nums[n];
n++;
}
return n;
}
}
反思:
在这一题中我加入了一个判断:
if(i >= nums.length) {
break;
}
刚开始是没有这个判断的,但是遇到一种情况就是例如[1, 1, 1]这个数组,在第一次循环的时候i就会一直遍历到最后并且值为3,如果没有这个判断在后面获取nums[i]的值时就会出现数组越界的问题。
11、移动零
题目:
我的思路:
这一题因为仍然是原地操作,所以不能够定义新的数组。我的思路和上一题删除数组重复项是类似的,定义两个指针i和j,i负责遍历整个数组,当i指向0时,j指针从i开始向后移动判断有几个连续的0,j指针直到遇到非0值时再停止移动,然后交换i指向的值和j指向的值即可。
按照这个思路实现的代码如下:
class Solution {
public void moveZeroes(int[] nums) {
if(nums == null || nums.length == 0 || nums.length == 1) {
return;
}
for(int i = 0; i < nums.length; i++) {
if(nums[i] == 0) {
int j = i;
//1、遍历有多少个0
while(j < nums.length && nums[j] == 0) {
j++;
}
//2、到最后了,直接退出
if(j == nums.length) {
break;
}
//3、交换j位的数和i位的0
nums[i] = nums[j];
nums[j] = 0;
}
}
}
}
反思:
这一题我仍然增加了j是否遍历到最后的判断,这还是为了防止出现数组越界的问题。另外我的解决方法是比较耗时的,因为如果出现重复的0的情况,例如[0, 0, 0, 1, 2],这样替换了两次之后结果为[1, 2, 0, 0, 0],i指向的是数组的第三位,因为i没有遍历到最后,所以仍然要继续循环,时间复杂度就增加了。