Python实现经典排序算法--堆排序

上次说到了经典算法选择排序，感觉是比较简单的算法，这一次说一说稍微有点难度的堆排序。

堆排序的时间复杂度要明显优于前面的冒泡排序，插入排序和选择排序（局限于n较大时）。

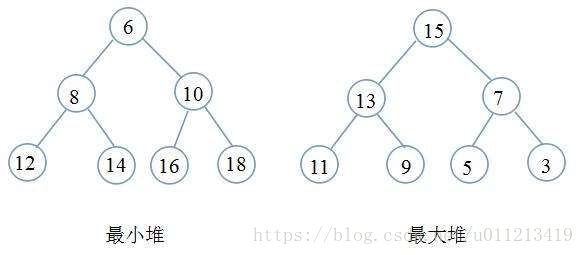
1、堆（二叉堆）

先来讲讲堆（二叉堆），是一个数组，它可以近似被看作是一个完全二叉树。树上每一个节点对应一个元素，除了最底层外，该树是完全充满的，而且是从左至右填充的，所有最底层的元素会从左向右填充。表示堆的数组list包括两个属性，list.length表示数组的个数，list.heap_size则表示有多少个堆元素存储在该数组中。也就是0<=list.heap_size<=list.length，list中可能存在若干个元素不是堆元素，在讲堆性质的时候会举例说明。

2、堆性质

二叉堆有两种形式，最大堆和最小堆，但其实本身性质是一样的，就和从小到大排序和从大到小排序一样。

最大堆性质是指除了根以外的所有节点，都要满足：

list[PARENT(i)] >= list[i]

最小堆性质要满足：

list[PARENT(i)] <= list[i]

3、堆高度

如果把堆看作是一棵树，堆高度就是指的堆中节点的高度，即为根节点到叶节点最长简单路径上的数目。对于一个元素数量为n的list，其堆高度为floor(lg n)。

下面来证明一下：在高度为h的堆中，元素最多的应该是当底层全满时，即：1+2+2^2+……+2^h=2^(h+1)-1

                                                  元素最少的应该是当底层只有一个元素时，即：1+2+……+2^(h-1)+1=2^h

则有：2^h<=n<=2^(h+1)-1,分别对不等式里面取对数lg，既有lg(2^h)<=lg n<=lg(2^(h+1)-1)，则有h<=lg n

4、堆排序的算法实现

其实堆排序就只有两种过程，一个是建堆，一个是堆的维护，建堆的历遍的过程，而维护则是递归的过程。在这里维护是底层，而历遍是顶层。我们先来看看维护，以求解最大堆为例，先定义一个初始化的根节点，这里我们选择root=length//2，来作为初始化值，left=2*root（左结点），right=left+1（右结点），堆维护实质上就是通过不断的交换顺序来保证堆的性质。即判断根结点与左结点、右结点的最大值，如果左结点的值最大，则与根结点交换位置，若是右结点的值最大，则与根结点交换位置，否则该结点即为根结点，左结点，右结点的最大值，传递根结点下标到下一次递归，直到找到list中的最大根结点。而顶层循环则是倒序历遍lenth//2，这样足以完成所有元素的调用，甚至可以为(length-2)//2，终止条件是当根结点的下标为0时，结点1已经为最大堆的根节点了，此时循环结束。但是到这一步还不够，这一步仅仅是能确保下标为0的结点1为根结点，即只能确保list[0]为根节点，通过讲该根节点与list[list.szie]进行互换，去掉根节点，形成一个新堆，长度为length-=1，构造新堆后，在利用堆维护性质来获取新堆的根节点，依次的我们可以结点提取出来，形成一个序列，这就是我们要求的序列。以下是用Python实现经典插入排序的code。这里的时间复杂度为omiga（n*lg n)

def heapsort(list):
	if list!=None:
		if list==1:
			pass
		else:
			for start in range((len(list))//2,-1,-1):#顶层循环第一步，找到堆的根结点
				rootsort(list,start,len(list)-1)
			for end in range(len(list)-1,-1,-1):#顶层循环第二步，讲根结点依次提取并排序
					list[0],list[end]=list[end],list[0]
					end-=1
					rootsort(list,0,end)
	print (list)
def rootsort(list,root,end):#递归函数，对list做最大堆调整
	left=2*root #父结点的左结点
	right=left+1#父结点的右结点
	if left<=end and list[root]

out:[1, 2, 4, 4, 7, 8, 9, 10, 14, 16]

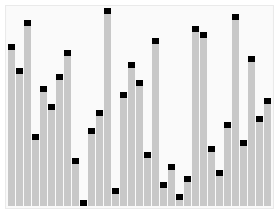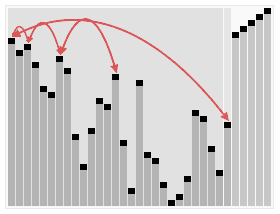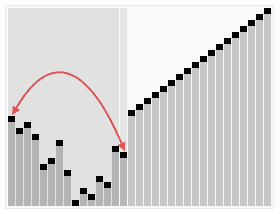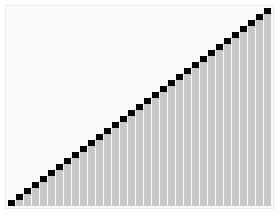
上面过程可以用网络上的一张图片进行描述：

这里我再详细将每一次求根结点过程展示一下：

def heapsort(list):
	if list!=None:
		if list==1:
			pass
		else:
			for start in range((len(list))//2,-1,-1):
				print(start)
				rootsort(list,start,len(list)-1)
			for end in range(len(list)-1,-1,-1):
					list[0],list[end]=list[end],list[0]
					print ('*',end,'*')
					print ('^',list,'^')
					end-=1
					rootsort(list,0,end)
	print (list)
def rootsort(list,root,end):
	left=2*root 
	right=left+1
	if left<=end and list[root]

out：

5
4
3
" 3 "
[4, 1, 4, 14, 16, 9, 10, 2, 8, 7]
2
" 2 "
[4, 1, 16, 14, 4, 9, 10, 2, 8, 7]
" 4 "
[4, 1, 16, 14, 8, 9, 10, 2, 4, 7]
1
" 1 "
[4, 16, 1, 14, 8, 9, 10, 2, 4, 7]
" 2 "
[4, 16, 9, 14, 8, 1, 10, 2, 4, 7]
0
" 0 "
[16, 4, 9, 14, 8, 1, 10, 2, 4, 7]
" 1 "
[16, 14, 9, 4, 8, 1, 10, 2, 4, 7]
" 3 "
[16, 14, 9, 10, 8, 1, 4, 2, 4, 7]
* 9 *
^ [7, 14, 9, 10, 8, 1, 4, 2, 4, 16] ^
" 0 "
[14, 7, 9, 10, 8, 1, 4, 2, 4, 16]
" 1 "
[14, 10, 9, 7, 8, 1, 4, 2, 4, 16]
* 8 *
^ [4, 10, 9, 7, 8, 1, 4, 2, 14, 16] ^
" 0 "
[10, 4, 9, 7, 8, 1, 4, 2, 14, 16]
" 1 "
[10, 9, 4, 7, 8, 1, 4, 2, 14, 16]
" 2 "
[10, 9, 8, 7, 4, 1, 4, 2, 14, 16]
* 7 *
^ [2, 9, 8, 7, 4, 1, 4, 10, 14, 16] ^
" 0 "
[9, 2, 8, 7, 4, 1, 4, 10, 14, 16]
" 1 "
[9, 8, 2, 7, 4, 1, 4, 10, 14, 16]
" 2 "
[9, 8, 4, 7, 2, 1, 4, 10, 14, 16]
* 6 *
^ [4, 8, 4, 7, 2, 1, 9, 10, 14, 16] ^
" 0 "
[8, 4, 4, 7, 2, 1, 9, 10, 14, 16]
" 1 "
[8, 7, 4, 4, 2, 1, 9, 10, 14, 16]
* 5 *
^ [1, 7, 4, 4, 2, 8, 9, 10, 14, 16] ^
" 0 "
[7, 1, 4, 4, 2, 8, 9, 10, 14, 16]
" 1 "
[7, 4, 1, 4, 2, 8, 9, 10, 14, 16]
" 2 "
[7, 4, 2, 4, 1, 8, 9, 10, 14, 16]
* 4 *
^ [1, 4, 2, 4, 7, 8, 9, 10, 14, 16] ^
" 0 "
[4, 1, 2, 4, 7, 8, 9, 10, 14, 16]
" 1 "
[4, 4, 2, 1, 7, 8, 9, 10, 14, 16]
* 3 *
^ [1, 4, 2, 4, 7, 8, 9, 10, 14, 16] ^
" 0 "
[4, 1, 2, 4, 7, 8, 9, 10, 14, 16]
" 1 "
[4, 2, 1, 4, 7, 8, 9, 10, 14, 16]
* 2 *
^ [1, 2, 4, 4, 7, 8, 9, 10, 14, 16] ^
" 0 "
[2, 1, 4, 4, 7, 8, 9, 10, 14, 16]
* 1 *
^ [1, 2, 4, 4, 7, 8, 9, 10, 14, 16] ^
* 0 *
^ [1, 2, 4, 4, 7, 8, 9, 10, 14, 16] ^
[1, 2, 4, 4, 7, 8, 9, 10, 14, 16]