大话数据结构学习笔记 - 图的最小生成树之Kruskal算法

大话数据结构学习笔记 - 图的最小生成树之Kruskal算法

Kruskal算法

克鲁斯卡尔(Kruskal)算法，是用来求加权连通图的最小生成树的算法

大话数据结构定义

假设 N=(V,{E}) N = ( V , { E } ) 是连通网，则令最小生成树的初始状态为只有n个顶点而无边的非连通图 T={V,{}} T = { V , { } } 。图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量上，则将此边加入到T中，否则社区此边而选择下一条代价最小的边，以此类推，直至T中所有顶点都在同一连通分量上为止。

基本思想

按照权值从小到大的顺序选择n - 1条边，并保证这n - 1条边不构成回路

具体做法

首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林不产生回路，直至森林变成过一棵树为止

Kruskal算法图解

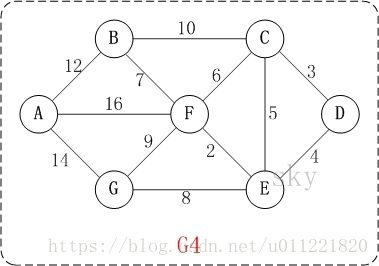
以上图G4为例，使用克鲁斯卡尔算法进行演示实现最小生成树，用parent表示

第零步： 将邻接矩阵转换为边表数组，并且按权值大小排序

第一步： 将边 <E,F> < E , F > 加入最小生成树中

​ 边 <E,F> < E , F > 的权值最小，故将其加入最小生成树

第二步： 将边 <C,D> < C , D > 加入最小生成树中

​ 上一步操作后， 边 <C,D> < C , D > 的权值最小，故将其加入最小生成树

第三步： 将边 <D,E> < D , E > 加入最小生成树中

​ 上一步操作后， 边 <D,E> < D , E > 的权值最小，故将其加入最小生成树

第四步： 将边 <B,F> < B , F > 加入最小生成树中

​ 上一步操作后，边 <C,E> < C , E > 的权值最小， 但边 <C,E> < C , E > 会和最小生成树中的已有边构成回路，故跳过。同理，跳过边 <C,F> < C , F >

第五步：将边 <E,G> < E , G > 加入到最小生成树中

​ 上一步操作后，边 <E,G> < E , G > 的权值最小，故将其加入到最小生成树中

第六步： 将边 <A,B> < A , B > 加入到最小生成树中

​ 上一步操作后，边 <F,G> < F , G > 权值最小， 但会和已有边构成回路，跳过。同理跳过边 <B,C> < B , C > 。将边 <A,B> < A , B > 加入

此时，最小生成树构造完成，含有的依次为 <E,F><C,D><D,E><B,F><E,G><A,B> < E , F >< C , D >< D , E >< B , F >< E , G >< A , B >

Kruskal算法要点

1. 对图的所有边按照权值大小排序

   此问题可通过代码实例理解

2. 将边添加到最小生成树中，如何判断是否形成回路

   通过记录每个顶点在最小生成树中的终点。终点即在最小生成树中与它连通的最大顶点。每次添加一条边到最小生成树中时，判断该边的两个顶点的终点是否重合，重合则构成回路。

   

   在将 <E,F><C,D><D,E> < E , F >< C , D >< D , E > 加入到最小生成树中后，这几条边的顶点就都有了终点

   • C的终点是F
   • D的终点是F
   • E的终点是F
   • F的终点是F

   关于终点，就是将所有顶点按照从小到大的顺序排列好之后；某个顶点的终点就是”与它连通的最大顶点”。 虽然边 <C,E> < C , E > 权值最小，但终点都是F， 故会形成回路

Kruskal算法代码

Edge边集数组结构

typedef struct
{
    int begin;
    int end;
    int weight;
}Edge;

算法

/* 生成最小生成树 */
void MiniSpanTree_Kruskal(MGraph G)
{
    int i, j, n, m;
    int k = 0;
    int parent[MAXVEX];  /* 定义一数组用来判断边与边是否形成环路 */
    Edge edges[MAXEDGE];  /* 定义边集数组,edge的结构为begin,end,weight,均为整型 */

    /* 用来构建边集数组并排序********************* */
    for(i = 0; i < G.numVertexes - 1; i++)
    {
        for(j = i + 1; j < G.numVertexes; j++)
        {
            if(G.arc[i][j] < INF)
            {
                edges[k].begin = i;
                edges[k].end = j;
                edges[k].weight = G.arc[i][j];
                k++;
            }
        }
    }
    sort(edges, &G);
    /* ******************************************* */

    printf("打印最小生成树：\n");

    for(i = 0; i < G.numVertexes; i++)
        parent[i] = 0;  /* 初始化数组值为0 */

    for(i = 0; i < G.numEdges; i++)  /* 循环每一条边 */
    {
        n = Find(parent, edges[i].begin);
        m = Find(parent, edges[i].end);
        if(n != m)  /* 假如n与m不等，说明此边没有与现有的生成树形成环路 */
        {
            parent[n] = m;  /* 将此边的结尾顶点放入下标为起点的parent中。 表示此顶点已经在生成树集合中*/
            printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
        }
    }

}

算法源码

邻接矩阵源码

参考资料

• 大话数据结构
• Kruskal算法(一)之 C语言详解