深入理解Spark ML：基于ALS矩阵分解的协同过滤算法与源码分析

http://blog.csdn.net/u011239443/article/details/51752904

1. 引言

随着互联网的迅猛发展,为了满足人们在繁多的信息中获取自己需要内容的需求,个性化推荐应用而生。协同过滤推荐是其中运用最为成功的技术之一。其中,基于用户的最近邻法根据相似用户的评分来预测当前用户的评分。然而,在用户数量以及用户评分不足的情况下,该方法存在冷启动和数据稀疏的问题。为了解决这两个问题，业界提出了提出了基于项的最近邻法，利用项之间相似性稳定的特点可以离线计算相似性,降低了在线计算量,提高了推荐效率,但同样存在冷启动和数据稀疏问题。若使用 矩 阵 分 解 中 的 奇 异 值 分 解 ( Singular Value Decomposition,SVD) 减少评分矩阵的维数,之后应用最近邻法预测评分,一定程度上解决了同义词问题,但由于评分矩阵中大部分的评分是分解之前填充的,所以得到的特征矩阵不能直接用于评分。业界还提出了一种基于矩阵分解和用户近邻模型的算法,解决了数据稀疏的问题,但存在模型过拟合的问题。而协同过滤提出了一种支持不完整评分矩阵的矩阵分解方法,不用对评分矩阵进行估值填充,有很好的推荐精度。在 Netflix推荐系统竞赛中的应用表明,该矩阵分解相对于其他的推荐算法能产生更精确的推荐。 [1 2] [ 1   2 ]

在矩阵分解推荐算法中,每项评分预测都需要整合现有评分集的信息。随着用户数与项目数的增长,算法的计算量也会随着增长,单机模式的推荐算法逐渐难以满足算法的计算以及推送的即时性需求,因此分布式推荐算法成为推荐算法中研究的一个新的方向。业界提出了分布式的矩阵分解算法,为矩阵分解的并行计算提供了一种可行的解决方案,但其使用的MapReduce框架在各计算节点的迭代计算中会产生过多的磁盘文件读写操作,影响了算法的执行效率。

本文旨在深入与Spark并行计算框架结合,探索协同过滤算法原理与在Spark上的实现,来解决大数据情况下矩阵分解推荐算法时间代价过高的问题。

2. 基于ALS矩阵分解协同过滤算法

如上述提及的，协同过滤提出了一种支持不完整评分矩阵的矩阵分解方法,不用对评分矩阵进行估值填充,有很好的推荐精度。Spark MLlib中实现的基于ALS矩阵分解协同过滤算法。下面我们来介绍下ALS矩阵分解

2.1 矩阵分解模型

用户对物品的打分行为可以表示成一个评分矩阵A(m*n)，表示m个用户对n各物品的打分情况。如下表所示：

U\V	v1	v2	v3	v4
u1	4	3	?	5
u2	?	5	4	5
u3	?	?	3	3
u4	5	5	3	3
u5	2	1	5	?

其中， A(i,j) A ( i , j ) 表示用户 useri u s e r i 对物品 itemj i t e m j 的打分。但是，用户不会对所以物品打分，表中”？”表示用户没有打分的情况，所以这个矩阵A很多元素都是空的，我们称其为“缺失值（missing value）”。协同过滤提出了一种支持不完整评分矩阵的矩阵分解方法,不用对评分矩阵进行估值填充。在推荐系统中，我们希望得到用户对所有物品的打分情况，如果用户没有对一个物品打分，那么就需要预测用户是否会对该物品打分，以及会打多少分。这就是所谓的“矩阵补全（填空）”。

ALS 的核心假设是：打分矩阵A是近似低秩的，即一个 m∗n m ∗ n 的打分矩阵 A A 可以用两个小矩阵 U(m∗k) U ( m ∗ k ) 和 V(n∗k) V ( n ∗ k ) 的乘积来近似：

A≈UVT,k<<m,n A ≈ U V T , k << m , n

我们把打分理解成相似度，那么“打分矩阵 A(m∗n) A ( m ∗ n ) ”就可以由“用户喜好特征矩阵 U(m∗k) U ( m ∗ k ) ”和“产品特征矩阵 V(n∗k) V ( n ∗ k ) ”的乘积。

2.2 交替最小二乘法（ALS）

我们使用用户喜好特征矩阵 U(m∗k) U ( m ∗ k ) 中的第i个用户的特征向量 ui u i ，和产品特征矩阵 V(n∗k) V ( n ∗ k ) 第j个产品的特征向量 vj v j 来预测打分矩阵 A(m∗n) A ( m ∗ n ) 中的 aij a i j 。我们可以得出一下的矩阵分解模型的损失函数为：

C=∑(i,j)∈R[(aij−uivTj)2+λ(u2i+v2j)] C = ∑ ( i , j ) ∈ R [ ( a i j − u i v j T ) 2 + λ ( u i 2 + v j 2 ) ]

有了损失函数之后，下面就开始介绍优化方法。通常的优化方法分为两种：交叉最小二乘法（alternative least squares）和随机梯度下降法（stochastic gradient descent）。Spark使用的是交叉最小二乘法（ALS）来最优化损失函数。算法的思想就是：我们先随机生成然后固定它求解，再固定求解，这样交替进行下去，直到取得最优解 min(C) m i n ( C ) 。因为每步迭代都会降低误差，并且误差是有下界的，所以 ALS 一定会收敛。但由于问题是非凸的，ALS 并不保证会收敛到全局最优解。但在实际应用中，ALS 对初始点不是很敏感，是否全局最优解造成的影响并不大。

算法的执行步骤：

• 先随机生成一个。一般可以取0值或者全局均值。

• 固定，即认为是已知的常量，来求解：
  C=∑(i,j)∈R[(aij−u(0)ivTj)2+λ((u2i)(0)+v2j)] C = ∑ ( i , j ) ∈ R [ ( a i j − u i ( 0 ) v j T ) 2 + λ ( ( u i 2 ) ( 0 ) + v j 2 ) ]
  由于上式中只有 vj v j 一个未知变量，因此C的最优化问题转化为最小二乘问题，用最小二乘法求解 vj v j 的最优解：
  固定 j,j∈(1,2,...,n) j , j ∈ ( 1 , 2 , . . . , n ) ，则：等式两边关于为 vj v j 求导得：

  d(c)d(vj) d ( c ) d ( v j )
  =dd(vj)(∑i=1m[(aij−u(0)ivTj)2+λ((u2i)(0)+v2j)]) = d d ( v j ) ( ∑ i = 1 m [ ( a i j − u i ( 0 ) v j T ) 2 + λ ( ( u i 2 ) ( 0 ) + v j 2 ) ] )
  =∑i=1m[2(aij−u(0)ivTj)(−(uTi)(0))+2λvj] = ∑ i = 1 m [ 2 ( a i j − u i ( 0 ) v j T ) ( − ( u i T ) ( 0 ) ) + 2 λ v j ]
  =2∑i=1m[(u(0)i(uTi)(0)+λ)vj−aij(uTi)(0)] = 2 ∑ i = 1 m [ ( u i ( 0 ) ( u i T ) ( 0 ) + λ ) v j − a i j ( u i T ) ( 0 ) ]

  令 d(c)d(vj)=0 d ( c ) d ( v j ) = 0 ，可得：
  ∑i=1m[(u(0)i(uTi)(0)+λ)vj]=∑i=1maij(uTi)(0) ∑ i = 1 m [ ( u i ( 0 ) ( u i T ) ( 0 ) + λ ) v j ] = ∑ i = 1 m a i j ( u i T ) ( 0 )
  =>(U(0)(UT)(0)+λE)vj=aTjU(0) => ( U ( 0 ) ( U T ) ( 0 ) + λ E ) v j = a j T U ( 0 )

  令 M1=U(0)(UT)(0)+λE,M2=aTjU(0) M 1 = U ( 0 ) ( U T ) ( 0 ) + λ E , M 2 = a j T U ( 0 ) ，则 vj=M−11M2 v j = M 1 − 1 M 2
  按照上式依次计算 v1，v2，...，vn v 1 ， v 2 ， . . . ， v n ，从而得到 V(0) V ( 0 )

• 同理，用步骤2中类似的方法:
  C=∑(i,j)∈R[(aij−ui(vTj)(0))2+λ(u2i+(v2j)(0))] C = ∑ ( i , j ) ∈ R [ ( a i j − u i ( v j T ) ( 0 ) ) 2 + λ ( u i 2 + ( v j 2 ) ( 0 ) ) ]
  固定 i,i∈(1,2,...,m) i , i ∈ ( 1 , 2 , . . . , m ) ，则：等式两边关于为 ui u i 求导得：

  d(c)d(ui) d ( c ) d ( u i )
  =dd(ui)(∑j=1n[(aij−ui(vTj)(0))2+λ((u2i)+(v2j)(0))]) = d d ( u i ) ( ∑ j = 1 n [ ( a i j − u i ( v j T ) ( 0 ) ) 2 + λ ( ( u i 2 ) + ( v j 2 ) ( 0 ) ) ] )
  =∑j=1n[2(aij−ui(vTj)(0))(−(vTj)(0))+2λui] = ∑ j = 1 n [ 2 ( a i j − u i ( v j T ) ( 0 ) ) ( − ( v j T ) ( 0 ) ) + 2 λ u i ]
  =2∑j=1n[(v(0)j(vTj)(0)+λ)ui−aij(vTj)(0)] = 2 ∑ j = 1 n [ ( v j ( 0 ) ( v j T ) ( 0 ) + λ ) u i − a i j ( v j T ) ( 0 ) ]

  令 d(c)d(ui)=0 d ( c ) d ( u i ) = 0 ，可得：
  ∑j=1n[(v(0)j(vTj)(0)+λ)ui]=∑j=1naij(vTj)(0) ∑ j = 1 n [ ( v j ( 0 ) ( v j T ) ( 0 ) + λ ) u i ] = ∑ j = 1 n a i j ( v j T ) ( 0 )
  =>((V(0)(VT)(0)+λE)ui=aTiV(0) => ( ( V ( 0 ) ( V T ) ( 0 ) + λ E ) u i = a i T V ( 0 )
  令 M1=V(0)(VT)(0)+λE,M2=aTiV(0) M 1 = V ( 0 ) ( V T ) ( 0 ) + λ E , M 2 = a i T V ( 0 ) ，则 ui=M−11M2 u i = M 1 − 1 M 2
  按照上式依次计算 u1，u2，...，un u 1 ， u 2 ， . . . ， u n ，从而得到 U(1) U ( 1 )

• 循环执行步骤2、3，直到损失函数C的值收敛（或者设置一个迭代次数N，迭代执行步骤2、3，N次后停止）。这样，就得到了C最优解对应的矩阵U、V。

2.3 显示反馈与隐式反馈

推荐系统依赖不同类型的输入数据，最方便的是高质量的显式反馈数据，它们包含用户对感兴趣商品明确的评价。例如，Netflix收集的用户对电影评价的星星等级数据。但是显式反馈数据不一定总是找得到，因此推荐系统可以从更丰富的隐式反馈信息中推测用户的偏好。

隐式反馈类型包括购买历史、浏览历史、搜索模式甚至鼠标动作。例如，购买同一个作者许多书的用户可能喜欢这个作者。

许多研究都集中在处理显式反馈，然而在很多应用场景下，应用程序重点关注隐式反馈数据。因为可能用户不愿意评价商品或者由于系统限制我们不能收集显式反馈数据。在隐式模型中，一旦用户允许收集可用的数据，在客户端并不需要额外的显式数据。

了解隐式反馈的特点非常重要，因为这些特质使我们避免了直接调用基于显式反馈的算法。最主要的特点有如下几种：

• 没有负反馈。通过观察用户行为，我们可以推测那个商品他可能喜欢，然后购买，但是我们很难推测哪个商品用户不喜欢。这在显式反馈算法中并不存在，因为用户明确告诉了我们哪些他喜欢哪些他不喜欢。
• 隐式反馈是内在的噪音。虽然我们拼命的追踪用户行为，但是我们仅仅只是猜测他们的偏好和真实动机。例如，我们可能知道一个人的购买行为，但是这并不能完全说明偏好和动机，因为这个商品可能作为礼物被购买而用户并不喜欢它。
• 显示反馈的数值值表示偏好（preference），隐式回馈的数值值表示信任（confidence）。基于显示反馈的系统用星星等级让用户表达他们的喜好程度，例如一颗星表示很不喜欢，五颗星表示非常喜欢。基于隐式反馈的数值值描述的是动作的频率，例如用户购买特定商品的次数。一个较大的值并不能表明更多的偏爱。但是这个值是有用的，它描述了在一个特定观察中的信任度。
  一个发生一次的事件可能对用户偏爱没有用，但是一个周期性事件更可能反映一个用户的选择。
• 评价隐式反馈推荐系统需要合适的手段。

2.3.1 显式反馈模型

潜在因素模型由一个针对协同过滤的交替方法组成，它以一个更加全面的方式发现潜在特征来解释观察的ratings数据。我们关注的模型由奇异值分解（SVD）推演而来。一个典型的模型将每个用户 u u （包含一个用户-因素向量 ui u i ）和每个商品 v v （包含一个用户-因素向量 vj v j ）联系起来。
预测通过内积 rij=(uT)ivj r i j = ( u T ) i v j 来实现。另一个需要关注的地方是参数估计。许多当前的工作都应用到了显式反馈数据集中，这些模型仅仅基于观察到的rating数据直接建模，同时通过一个适当的正则化来避免过拟合。公式就如上一节所提到的：

minu,v∑(i,j)∈R[(aij−uivTj)2+λ(u2i+v2j)] m i n u , v ∑ ( i , j ) ∈ R [ ( a i j − u i v j T ) 2 + λ ( u i 2 + v j 2 ) ]

2.3.2 隐式反馈模型

在显式反馈的基础上，我们需要做一些改动得到我们的隐式反馈模型。首先，我们需要形式化由 rij r i j 变量衡量的信任度的概念。我们引入了一组二元变量 pij p i j ，它表示用户 u u 对商品 v v 的偏好。 pij p i j 的公式如下：

pij={1,rij>00,rij=0 p i j = { 0 , r i j = 0 1 , r i j > 0

换句话说，如果用户购买了商品，我们认为用户喜欢该商品，否则我们认为用户不喜欢该商品。然而我们的信念（beliefs）与变化的信任（confidence）等级息息相关。首先，很自然的，pij的值为0和低信任有关。用户对一个商品没有得到一个正的偏好可能源于多方面的原因，并不一定是不喜欢该商品。例如，用户可能并不知道该商品的存在。
另外，用户购买一个商品也并不一定是用户喜欢它。因此我们需要一个新的信任等级来显示用户偏爱某个商品。一般情况下， rij r i j 越大，越能暗示用户喜欢某个商品。因此，我们引入了一组变量 cij c i j ，它衡量了我们观察到pij的信任度。 cij c i j 一个合理的选择如下所示：

cij=1+αrij c i j = 1 + α r i j

按照这种方式，我们存在最小限度的信任度，并且随着我们观察到的正偏向的证据越来越多，信任度也会越来越大。

我们的目的是找到用户向量 ui u i 以及商品向量 vj v j 来表明用户偏好。这些向量分别是用户因素（特征）向量和商品因素（特征）向量。本质上，这些向量将用户和商品映射到一个公用的隐式因素空间，从而使它们可以直接比较。这和用于显式数据集的矩阵分解技术类似，但是包含两点不一样的地方：
（1）我们需要考虑不同的信任度
（2）最优化需要考虑所有可能的u，v对，而不仅仅是和观察数据相关的u，v对。因此，通过最小化下面的损失函数来计算相关因素（factors）:
minu,v∑(i,j)∈R[cij(aij−uivTj)2+λ(u2i+v2j)] m i n u , v ∑ ( i , j ) ∈ R [ c i j ( a i j − u i v j T ) 2 + λ ( u i 2 + v j 2 ) ]

3. Spark MLlib ALS

在接下来的实例中, 我们将加载来着MovieLens数据集, 每行包含了用户ID, 电影ID,该用户对该电影的评分以及时间戳.

3.1 训练模型

import org.apache.spark.ml.evaluation.RegressionEvaluator
import org.apache.spark.ml.recommendation.ALS

case class Rating(userId: Int, movieId: Int, rating: Float, timestamp: Long)
def parseRating(str: String): Rating = {
  val fields = str.split("::")
  assert(fields.size == 4)
  Rating(fields(0).toInt, fields(1).toInt, fields(2).toFloat, fields(3).toLong)
}

val ratings = spark.read.textFile("data/mllib/als/sample_movielens_ratings.txt")
  .map(parseRating)
  .toDF()
val Array(training, test) = ratings.randomSplit(Array(0.8, 0.2))

val als = new ALS()
  .setRank(12)
  .setMaxIter(50)
  .setRegParam(0.01)
  .setUserCol("userId")
  .setItemCol("movieId")
  .setRatingCol("rating")
val model = als.fit(training)

val predictions = model.transform(test)

• Rank: 对应ALS模型中的因子个数，即矩阵分解出的两个矩阵的新的行/列数，即 A≈UVT,k<<m,n A ≈ U V T , k << m , n 中的k。
• MaxIter: 对应运行时的最大迭代次数
• RegParam: 控制模型的正则化过程，从而控制模型的过拟合情况。

3.2 基于物品的推荐系统

物品推荐，给定一个物品，哪些物品和它最相似。这里我们使用余弦相似度。假设现在我们有一个测试集特征向量A和一个训练集的特征向量B：

A：[1, 2, 2, 1, 1, 1, 0]
B：[1, 2, 2, 1, 1, 2, 1]

到这里，问题就变成了如何计算这两个向量的相似程度。我们可以把它们想象成空间中的两条线段，都是从原点（[0, 0, …]）出发，指向不同的方向。两条线段之间形成一个夹角，如果夹角为0度，意味着方向相同、线段重合；如果夹角为90度，意味着形成直角，方向完全不相似；如果夹角为180度，意味着方向正好相反。因此，我们可以通过夹角的大小，来判断向量的相似程度。夹角越小，就代表越相似。

以二维空间为例，上图的a和b是两个向量，我们要计算它们的夹角θ。余弦定理告诉我们，可以用下面的公式求得：

cosΘ=x1x2+y1y2x21+y21‾‾‾‾‾‾√∗x22+y22‾‾‾‾‾‾√ c o s Θ = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 ∗ x 2 2 + y 2 2

拓展到n维向量，假定A和B是两个n维向量，A是 [A1, A2, …, An] ，B是 [B1, B2, …, Bn] ，则A与B的夹角θ的余弦等于：

cosΘ=Σni=1(Ai∗Bi)Σni=1(Ai)2‾‾‾‾‾‾‾‾‾√∗Σni=1(Bi)2‾‾‾‾‾‾‾‾‾√=A⋅B|A|∗|B| c o s Θ = Σ i = 1 n ( A i ∗ B i ) Σ i = 1 n ( A i ) 2 ∗ Σ i = 1 n ( B i ) 2 = A ⋅ B | A | ∗ | B |

使用这个公式，我们就可以得到，特征向量A与特征向量B的夹角的余弦：

cosΘ=1∗1+2∗2+2∗2+1∗1+1∗1+1∗2+0∗112+22+22+12+12+12+02‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√∗12+22+22+12+12+22+12‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√=1312‾‾‾√∗16‾‾‾√=0.938 c o s Θ = 1 ∗ 1 + 2 ∗ 2 + 2 ∗ 2 + 1 ∗ 1 + 1 ∗ 1 + 1 ∗ 2 + 0 ∗ 1 1 2 + 2 2 + 2 2 + 1 2 + 1 2 + 1 2 + 0 2 ∗ 1 2 + 2 2 + 2 2 + 1 2 + 1 2 + 2 2 + 1 2 = 13 12 ∗ 16 = 0.938

余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫”余弦相似度”

我们这个方案，计算出一条测试集的特征向量与训练集各个特征向量的余弦相似度，将该条测试集的类别标记为与其余弦相似度最大的训练集特征向量所对应的类别。

def cosineSimilarity(vec1: DoubleMatrix, vec2: DoubleMatrix): Double = {
    vec1.dot(vec2) / (vec1.norm2() * vec2.norm2())
}

import org.jblas.DoubleMatrix
val aMatrix = new DoubleMatrix(Array(1.0, 2.0, 3.0))

求各个产品的余弦相似度：

val sims = model.productFeatures.map{ case (id, factor) => 
    val factorVector = new DoubleMatrix(factor)
    val sim = cosineSimilarity(factorVector, itemVector)
    (id, sim)
}

求相似度最高的前10个相识电影。第一名肯定是自己，所以要取前11个，再除去第1个：

val sortedSims2 = sims.top(K + 1)(Ordering.by[(Int, Double), Double] { case (id, similarity) => similarity })
sortedSims2.slice(1, 11).map{ case (id, sim) => (titles(id), sim) }.mkString("\n")
/* 
(Hideaway (1995),0.6932331537649621)
(Body Snatchers (1993),0.6898690594544726)
(Evil Dead II (1987),0.6897964975027041)
(Alien: Resurrection (1997),0.6891221044611473)
(Stephen King's The Langoliers (1995),0.6864214133620066)
(Liar Liar (1997),0.6812075443259535)
(Tales from the Crypt Presents: Bordello of Blood (1996),0.6754663844488256)
(Army of Darkness (1993),0.6702643811753909)
(Mystery Science Theater 3000: The Movie (1996),0.6594872765176396)
(Scream (1996),0.6538249646863378)
*/

在ALS矩阵分解基础上，还有很多其他推荐系统实现的方式，这里就不在列举。

4. ALS矩阵分解算法并行化

有许多机器学习算法需要将这次迭代权值调优后的结果数据集作为下次迭代的输入，而使用MapReduce计算框架经过一次Reduce操作后输出数据结果写回磁盘，大大的降低的速度。我们所使用的ALS矩阵分解算法也是一种需要迭代的算法，如将上次计算得的 U(n) U ( n ) 代入下次计算 V(n) V ( n ) 操作中，再将 V(n) V ( n ) 带入下次计算 Un+1 U n + 1 的操作中，以此类推：

在Spark框架下的并行化,不同于MapReduce的并行化 [3] [ 3 ] 。Spark RDD允许用户在执行多个查询时显式地将工作集缓存在内存中，后续的查询能够重用工作集，这极大地提升了查询速度。RDD提供了一种高度受限的共享内存模型，即RDD是只读的记录分区的集合，只能通过在其他RDD执行确定的转换操作（如map、join和group by）而创建，然而这些限制使得实现容错的开销很低。

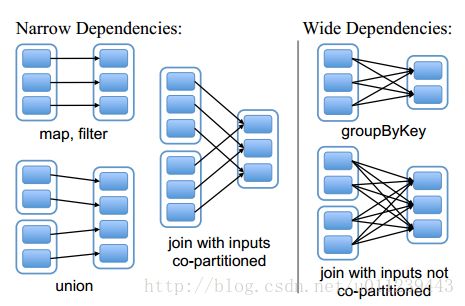
设计接口的一个关键问题就是，如何表示RDD之间的依赖。RDD之间的依赖关系可以分为两类，即：
（1）窄依赖（narrow dependencies）：子RDD的每个分区依赖于常数个父分区（即与数据规模无关）；
（2）宽依赖（wide dependencies）：子RDD的每个分区依赖于所有父RDD分区。例如，map产生窄依赖，而join则是宽依赖（除非父RDD被哈希分区） [4] [ 4 ] 。

我们也可以这样认为：

窄依赖指的是：每个parent RDD 的 partition 最多被 child RDD的一个partition使用
宽依赖指的是：每个parent RDD 的 partition 被多个 child RDD的partition使用

窄依赖每个child RDD 的partition的生成操作都是可以并行的，而宽依赖则需要所有的parent partition shuffle结果得到后再进行。

我们可以看到公式中： ∑i=1m[(u(n)i(uTi)(n)+λ)vj]=∑i=1maij(uTi)(n) ∑ i = 1 m [ ( u i ( n ) ( u i T ) ( n ) + λ ) v j ] = ∑ i = 1 m a i j ( u i T ) ( n ) ，若 parent RDD 中 u(n)i u i ( n ) 在上一迭代中已经计算出结果，并可以交给下个RDD来计算 v(n)j v j ( n ) 。 所以，parent RDD 和 child RDD 之间是窄依赖，不需要昂贵的shuffle，各个partition的任务可以并行执行。

5. ALS模型实现

基于Spark架构，我们可以将迭代算法ALS很好的并行化。本章将详细讲解Spark MLlib 中的ALS模型的实现。

val als = new ALS()
  .setRank(12)
  .setMaxIter(50)
  .setRegParam(0.01)
  .setUserCol("userId")
  .setItemCol("movieId")
  .setRatingCol("rating")
val model = als.fit(training)

val predictions = model.transform(test)

5.1 ALS.fit

首先，我们研究下ALS模型在设置好参数后，是如何fit训练集的：

 override def fit(dataset: Dataset[_]): ALSModel = {
    transformSchema(dataset.schema)        //(1)
    import dataset.sparkSession.implicits._

    val r = if ($(ratingCol) != "") col($(ratingCol)).cast(FloatType) else lit(1.0f) //（2）
    val ratings = dataset
      .select(checkedCast(col($(userCol)).cast(DoubleType)),
        checkedCast(col($(itemCol)).cast(DoubleType)), r)
      .rdd
      .map { row =>
        Rating(row.getInt(0), row.getInt(1), row.getFloat(2))
      }                                      //（3）
    val instrLog = Instrumentation.create(this, ratings) //（4）
    instrLog.logParams(rank, numUserBlocks, numItemBlocks, implicitPrefs, alpha,
                       userCol, itemCol, ratingCol, predictionCol, maxIter,
                       regParam, nonnegative, checkpointInterval, seed)   //（5）
    val (userFactors, itemFactors) = ALS.train(ratings, rank = $(rank),
      numUserBlocks = $(numUserBlocks), numItemBlocks = $(numItemBlocks),
      maxIter = $(maxIter), regParam = $(regParam), implicitPrefs = $(implicitPrefs),
      alpha = $(alpha), nonnegative = $(nonnegative),
      intermediateRDDStorageLevel = StorageLevel.fromString($(intermediateStorageLevel)),
      finalRDDStorageLevel = StorageLevel.fromString($(finalStorageLevel)),
      checkpointInterval = $(checkpointInterval), seed = $(seed))  //（6）
    val userDF = userFactors.toDF("id", "features")  //（7）
    val itemDF = itemFactors.toDF("id", "features")  //（8）
    val model = new ALSModel(uid, $(rank), userDF, itemDF).setParent(this) //（9）
    instrLog.logSuccess(model)  //（10）
    copyValues(model)  //（11）
  }

(1)： transformSchema函数最终会调用validateAndTransformSchema将dataset的中的validateAndTransformSchema，去检查用户ID、物品ID、评分是否都为数值，并为dataset新增predictionCol的列，其类型为Float。

(2)(3)：将dataset将用户ID和商品ID转为Int类型，将评分转为Double类型，并生成Rating RDD。

(4)(5)：生成训练时打印log的仪器并设置参数。

(6)(7)(8)：训练模型得到用户特征矩阵userFactors和物品特征矩阵itemFactors，并对列重命名得到userDF与itemDF。

(9)(10)(11)：传入rank, userDF, itemDF创建ALS模型。

5.2 ALS.train

这一节我们来深入研究下，上节代码（6）中是如何计算出用户特征矩阵userFactors和物品特征矩阵itemFactors的。接下来，我们来逐行分析。

5.2.1 参数

我们先来看下ALS.train的参数：

ALS.train

  def train[ID: ClassTag]( 
      ratings: RDD[Rating[ID]],
      rank: Int = 10,
      numUserBlocks: Int = 10,
      numItemBlocks: Int = 10,
      maxIter: Int = 10,
      regParam: Double = 1.0,
      implicitPrefs: Boolean = false,
      alpha: Double = 1.0,
      nonnegative: Boolean = false,
      intermediateRDDStorageLevel: StorageLevel = StorageLevel.MEMORY_AND_DISK,
      finalRDDStorageLevel: StorageLevel = StorageLevel.MEMORY_AND_DISK,
      checkpointInterval: Int = 10,
      seed: Long = 0L)(
      implicit ord: Ordering[ID]): (RDD[(ID, Array[Float])], RDD[(ID, Array[Float])]) = {
      ......
      }

以上定义中，

• ratings指用户提供的训练数据，它包括用户id集、商品id集以及相应的打分集。

  case class Rating[@specialized(Int, Long) ID](user: ID, item: ID, rating: Float)

• rank表示隐含因素的数量，也即特征的数量。
• numUserBlocks和numItemBlocks分别指用户和商品的块数量，即分区数量。
• regParam表示最小二乘法中lambda值的大小。
• implicitPrefs表示我们的训练数据是否是隐式反馈数据。
• Nonnegative表示求解的最小二乘的值是否是非负,根据Nonnegative的值的不同，spark使用了不同的求解方法。

5.2.2 初始化ALSPartitioner和LocalIndexEncoder

ALS.train

    require(intermediateRDDStorageLevel != StorageLevel.NONE,
      "ALS is not designed to run without persisting intermediate RDDs.")
    val sc = ratings.sparkContext
    val userPart = new ALSPartitioner(numUserBlocks)
    val itemPart = new ALSPartitioner(numItemBlocks)
    val userLocalIndexEncoder = new LocalIndexEncoder(userPart.numPartitions)
    val itemLocalIndexEncoder = new LocalIndexEncoder(itemPart.numPartitions)

• ALSPartitioner实现了基于hash的分区，它根据用户或者商品id的hash值来进行分区。ALSPartitioner即HashPartitioner：

 private[recommendation] type ALSPartitioner = org.apache.spark.HashPartitioner

class HashPartitioner(partitions: Int) extends Partitioner {
  require(partitions >= 0, s"Number of partitions ($partitions) cannot be negative.")

  def numPartitions: Int = partitions

  def getPartition(key: Any): Int = key match {
    case null => 0
    case _ => Utils.nonNegativeMod(key.hashCode, numPartitions)
  }

  override def equals(other: Any): Boolean = other match {
    case h: HashPartitioner =>
      h.numPartitions == numPartitions
    case _ =>
      false
  }

  override def hashCode: Int = numPartitions
}

• LocalIndexEncoder对（blockid，localindex）即（分区id，分区内索引）进行编码，并将其转换为一个整数，这个整数在高位存分区ID，在低位存对应分区的索引，在空间上尽量做到了不浪费。同时也可以根据这个转换的整数分别获得blockid和localindex。这两个对象在后续的代码中会用到。

  private[recommendation] class LocalIndexEncoder(numBlocks: Int) extends Serializable {

    require(numBlocks > 0, s"numBlocks must be positive but found $numBlocks.")

    private[this] final val numLocalIndexBits =
      math.min(java.lang.Integer.numberOfLeadingZeros(numBlocks - 1), 31)
    private[this] final val localIndexMask = (1 << numLocalIndexBits) - 1

    /** 将一个(blockId, localIndex) 在一个 integer 中编码 */
    def encode(blockId: Int, localIndex: Int): Int = {
      require(blockId < numBlocks)
      require((localIndex & ~localIndexMask) == 0)
      (blockId << numLocalIndexBits) | localIndex
    }

    /** 从编码的index得到 block id */
    @inline
    def blockId(encoded: Int): Int = {
      encoded >>> numLocalIndexBits
    }

    /**  从编码的index得到 local index */
    @inline
    def localIndex(encoded: Int): Int = {
      encoded & localIndexMask
    }
  }

5.2.3 根据nonnegative参数选择解决矩阵分解的方法

ALS.train

    val solver = if (nonnegative) new NNLSSolver else new CholeskySolver

如果需要解的值为非负,即nonnegative为true，那么用非负最小二乘（NNLS）来解，如果没有这个限制，用乔里斯基（Cholesky）分解来解。优化器的工作原理我们会在后续讲解。

5.2.4 将ratings数据转换为分区的格式

ALS.train

    val blockRatings = partitionRatings(ratings, userPart, itemPart)
      .persist(intermediateRDDStorageLevel)

将ratings数据转换为分区的形式，即（（用户分区id，商品分区id），分区数据集blocks））的形式，并缓存到内存中。其中分区id的计算是通过ALSPartitioner的getPartitions方法获得的，分区数据集由RatingBlock组成，

它表示（用户分区id，商品分区id ）对所对应的用户id集，商品id集，以及打分集，即（用户id集，商品id集，打分集）。

我们来看下partitionRatings：

  private def partitionRatings[ID: ClassTag](
      ratings: RDD[Rating[ID]],
      srcPart: Partitioner,
      dstPart: Partitioner): RDD[((Int, Int), RatingBlock[ID])] = {
      // 计算总共的分区数，默认的 10 × 10
    val numPartitions = srcPart.numPartitions * dstPart.numPartitions
    // 对ratings的每个分区进行操作
    ratings.mapPartitions { iter =>
    // 用numPartitions个RatingBlockBuilder[ID]一维数组来模拟RatingBlockBuilder[ID]矩阵
      val builders = Array.fill(numPartitions)(new RatingBlockBuilder[ID])
      // 对同一分区中每个ratings值操作
      iter.flatMap { r =>
        // 得到用户分区id
        val srcBlockId = srcPart.getPartition(r.user)
        // 得到商品分区id
        val dstBlockId = dstPart.getPartition(r.item)
        // 计算出对应的RatingBlockBuilder[ID]数组中的id
        val idx = srcBlockId + srcPart.numPartitions * dstBlockId
        // 得到该 RatingBlockBuilder
        val builder = builders(idx)
        // 将 该 ratings值 加入 该builder
        builder.add(r)
        // 若该builder>=2048 
        if (builder.size >= 2048) { // 2048 * (3 * 4) = 24k
        // 
          builders(idx) = new RatingBlockBuilder
        // 得到结果
          Iterator.single(((srcBlockId, dstBlockId), builder.build()))
        } else {
          Iterator.empty
        }
      } ++ {
        //上步结束后，若builders有还存在着ratings值builder
        builders.view.zipWithIndex.filter(_._1.size > 0).map { case (block, idx) =>
        // 根据 RatingBlockBuilder[ID]数组中的id 反推出 用户分区id和商品分区id
          val srcBlockId = idx % srcPart.numPartitions
          val dstBlockId = idx / srcPart.numPartitions
          // 得到结果
          ((srcBlockId, dstBlockId), block.build())
        }
      }
      // 根据 （用户分区id，商品分区id） 为key 进行聚合
      // 然后对 每个值Value 中的 blocks 操作
    }.groupByKey().mapValues { blocks =>
      val builder = new RatingBlockBuilder[ID]
      //  将每个block 合并 到 builder
      blocks.foreach(builder.merge)
      // 得到合并后的结果
      builder.build()
    }.setName("ratingBlocks")
  }

5.2.5 获取inblocks和outblocks数据

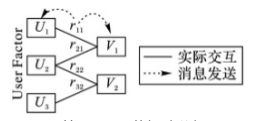
我们知道，通信复杂度是分布式实现一个算法时要重点考虑的问题，不同的实现可能会对性能产生很大的影响。我们假设最坏的情况：即求解商品需要的所有用户特征都需要从其它节点获得。 如下图所示：

求解v1需要获得u1,u2，求解v2需要获得u1,u2,u3等，在这种假设下，每步迭代所需的交换数据量是O(m*rank)，其中m表示所有观察到的打分集大小，rank表示特征数量。

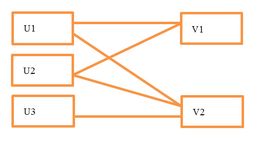
我们知道，如果计算v1和v2是在同一个分区上进行的，那么我们只需要把u1和u2一次发给这个分区就好了，而不需要将u1和u2分别发给v1,v2，这样就省掉了不必要的数据传输。

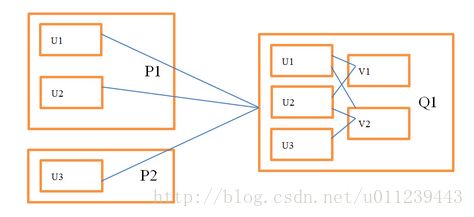
下图描述了如何在分区的情况下通过U来求解V，注意节点之间的数据交换量减少了：

使用这种分区结构，我们需要在原始打分数据的基础上额外保存一些信息。

在Q1中，我们需要知道和v1相关联的用户向量及其对应的打分，从而构建最小二乘问题并求解。这部分数据不仅包含原始打分数据，还包含从每个用户分区收到的向量排序信息，在代码里称作InBlock。

在P1中，我们要知道把u1,u2发给Q1。我们可以查看和u1相关联的所有产品来确定需要把u1发给谁，但每次迭代都扫一遍数据很不划算，所以在spark的实现中只计算一次这个信息，然后把结果通过RDD缓存起来重复使用。这部分数据我们在代码里称作OutBlock。

所以从U求解V，我们需要通过用户的OutBlock信息把用户向量发给商品分区，然后通过商品的InBlock信息构建最小二乘问题并求解。从V求解U，我们需要商品的OutBlock信息和用户的InBlock信息。所有的InBlock和OutBlock信息在迭代过程中都通过RDD缓存。打分数据在用户的InBlock和商品的InBlock各存了一份，但分区方式不同。这么做可以避免在迭代过程中原始数据的交换。

下面介绍获取InBlock和OutBlock的方法。下面的代码用来分别获取用户和商品的InBlock和OutBlock：

ALS.train

    val (userInBlocks, userOutBlocks) =
      makeBlocks("user", blockRatings, userPart, itemPart, intermediateRDDStorageLevel)
    userOutBlocks.count()
    // 交换userBlockId和itemBlockId以及其对应的数据
    val swappedBlockRatings = blockRatings.map {
      case ((userBlockId, itemBlockId), RatingBlock(userIds, itemIds, localRatings)) =>
        ((itemBlockId, userBlockId), RatingBlock(itemIds, userIds, localRatings))
    }
    val (itemInBlocks, itemOutBlocks) =
      makeBlocks("item", swappedBlockRatings, itemPart, userPart, intermediateRDDStorageLevel)
    itemOutBlocks.count()

我们会以求商品的InBlock以及用户的OutBlock为例来分析makeBlocks方法。

5.2.5.1 InBlock

下面以求商品的InBlock为例子，则src将代表商品，dst代表着用户。看下makeBlocks方法中的InBlock部分：

    val inBlocks = ratingBlocks.map {
    // 这部分代码工作主要是：
    // 将用户id映射为该分区中的用户id。
      case ((srcBlockId, dstBlockId), RatingBlock(srcIds, dstIds, ratings)) =>
        val start = System.nanoTime()
        // 用 OpenHashSet 对用户id去重
        val dstIdSet = new OpenHashSet[ID](1 << 20)
        dstIds.foreach(dstIdSet.add)
        val sortedDstIds = new Array[ID](dstIdSet.size)
        var i = 0
        var pos = dstIdSet.nextPos(0)
        while (pos != -1) {
          sortedDstIds(i) = dstIdSet.getValue(pos)
          pos = dstIdSet.nextPos(pos + 1)
          i += 1
        }
        assert(i == dstIdSet.size)
        // 将用户id 排序
        Sorting.quickSort(sortedDstIds)
        val dstIdToLocalIndex = new OpenHashMap[ID, Int](sortedDstIds.length)
        i = 0
        // 建立用户id与分区中的用户id（从0开始：0,1,2...）的映射关系
        while (i < sortedDstIds.length) {
          dstIdToLocalIndex.update(sortedDstIds(i), i)
          i += 1
        }
        logDebug(
          "Converting to local indices took " + (System.nanoTime() - start) / 1e9 + " seconds.")
          //将用户id 映射为 该分区中的用户id
        val dstLocalIndices = dstIds.map(dstIdToLocalIndex.apply)
        // 返回结果为：（商品分区id，（用户分区id，商品id集合，分区中对应的用户id集合，打分集合）
        (srcBlockId, (dstBlockId, srcIds, dstLocalIndices, ratings))
        // srcPart的分区进行聚合
    }.groupByKey(new ALSPartitioner(srcPart.numPartitions))
    .mapValues { iter =>
    ......

可见spark代码实现中，并没有存储用户的真实id，而是存储的使用LocalIndexEncoder生成的编码，这样节省了空间，格式为UncompressedInBlock:（商品id集合，分区中对应的用户id集合，打分集合）， 如：

([v1, v2, v1, v2, v2], [ui1, ui1, ui2, ui2, ui3], [r11, r12, r21, r22, r32])。

这种结构仍旧有压缩的空间，spark调用compress方法将商品id进行排序（排序有两个好处，除了压缩以外，后文构建最小二乘也会因此受益）， 并且转换为（不重复的有序的商品id集合，商品位置偏移集合，分区中对应的用户id集合，打分集合）的形式，以获得更优的存储效率（代码中就是将矩阵的coo格式转换为csc格式，你可以更进一步了解矩阵存储，以获得更多信息）。 以这样的格式修改：

([v1, v2, v1, v2, v2], [ui1, ui1, ui2, ui2, ui3], [r11, r12, r21, r22, r32])

排序后得到：

([v1, v1 v2, v2, v2], [ui1, ui1, ui2, ui2, ui3], [r11, r12, r21, r22, r32])

最终得到的结果是：

([v1, v2], [0, 2, 5], [ui1, ui2, ui1, ui2, ui3], [r11, r21, r12, r22, r32])

其中[0, 2]指v1对应的打分的位置区间是[0, 2），v2对应的打分的位置区间是[2, 5）。

我们继续看mapValues中的代码 ：

      .mapValues { iter =>
        val builder =
          new UncompressedInBlockBuilder[ID](new LocalIndexEncoder(dstPart.numPartitions))
        iter.foreach { case (dstBlockId, srcIds, dstLocalIndices, ratings) =>
          builder.add(dstBlockId, srcIds, dstLocalIndices, ratings)
        }
        builder.build().compress()
      }.setName(prefix + "InBlocks")
      .persist(storageLevel)

下面我们就来看下compress方法是如何创建InBlock的：

    def compress(): InBlock[ID] = {
      val sz = length
      assert(sz > 0, "Empty in-link block should not exist.")
      // 商品id进行排序
      sort()
      val uniqueSrcIdsBuilder = mutable.ArrayBuilder.make[ID]
      val dstCountsBuilder = mutable.ArrayBuilder.make[Int]
      var preSrcId = srcIds(0)
      uniqueSrcIdsBuilder += preSrcId
      var curCount = 1
      var i = 1
      // 笔者认为这里的变量j是无用的
      var j = 0
      while (i < sz) {
        val srcId = srcIds(i)
        if (srcId != preSrcId) {
          uniqueSrcIdsBuilder += srcId
          dstCountsBuilder += curCount
          preSrcId = srcId
          j += 1
          curCount = 0
        }
        curCount += 1
        i += 1
      }
      dstCountsBuilder += curCount
      val uniqueSrcIds = uniqueSrcIdsBuilder.result()
      val numUniqueSrdIds = uniqueSrcIds.length
      val dstCounts = dstCountsBuilder.result()
      val dstPtrs = new Array[Int](numUniqueSrdIds + 1)
      var sum = 0
      i = 0
      while (i < numUniqueSrdIds) {
      // 计算偏移
        sum += dstCounts(i)
        i += 1
        dstPtrs(i) = sum
      }
      // 返回值InBlock中包含 （不重复的有序的商品id集合，商品位置偏移集合，分区中对应的用户id集合，打分集合）
      InBlock(uniqueSrcIds, dstPtrs, dstEncodedIndices, ratings)
    }

笔者认为上述的变量j是无用的

      var j = 0

该问题已经提交到Spark Github 并merged：https://github.com/apache/spark/commit/cca8680047bb2ec312ffc296a561abd5cbc8323c

5.2.5.2 OutBlock

下面以求用户的OutBlock为例子，则src将代表用户，dst代表着商品。看下makeBlocks方法中的OutBlock部分：

// 这里的inBlocks的格式为
// （用户分区id，（不重复的有序的用户id集合，用户位置偏移集合，分区中对应的商品id集合，打分集合））
    val outBlocks = inBlocks.mapValues { case InBlock(srcIds, dstPtrs, dstEncodedIndices, _) =>
      val encoder = new LocalIndexEncoder(dstPart.numPartitions)
      // activeIds是一个二维数组
      // 第一维是 商品的分区id
      // 第二位是 不重复的有序的用户id集合的位置的集合
      val activeIds = Array.fill(dstPart.numPartitions)(mutable.ArrayBuilder.make[Int])
      var i = 0
      // 用来记录 该用户的id是否已经加入activeIds了各个第一维度（商品的分区）中 
      val seen = new Array[Boolean](dstPart.numPartitions)
      // 遍历不重复的有序的用户id集合
      while (i < srcIds.length) {
      // 遍历用户id为i的用户所对应的所有商品id
        var j = dstPtrs(i)
        // 置全为否
        ju.Arrays.fill(seen, false)
        while (j < dstPtrs(i + 1)) {
        // 根据商品id得到商品分区id
          val dstBlockId = encoder.blockId(dstEncodedIndices(j))
          if (!seen(dstBlockId)) {
          // 该不重复的有序的用户id集合的位置 加入activeIds对应的商品分区下
            activeIds(dstBlockId) += i
            seen(dstBlockId) = true
          }
          j += 1
        }
        i += 1
      }
      activeIds.map { x =>
        x.result()
      }
    }.setName(prefix + "OutBlocks")
      .persist(storageLevel)

5.2.6 利用inblock和outblock信息构建最小二乘

交换最小二乘算法是分别固定用户特征矩阵和商品特征矩阵来交替计算下一次迭代的商品特征矩阵和用户特征矩阵

初始化后的userFactors的格式是（用户分区id，用户特征矩阵factors），其中factors是一个二维数组，第一维的长度是用户数，第二维的长度是rank数。初始化的值是异或随机数的F范式。itemFactors的初始化与此类似。

通过用户的OutBlock把用户信息发给商品分区，然后结合商品的InBlock信息构建最小二乘问题，我们就可以借此解得商品的极小解。反之，通过商品OutBlock把商品信息发送给用户分区，然后结合用户的InBlock信息构建最小二乘问题，我们就可以解得用户解：

ALS.train

    val seedGen = new XORShiftRandom(seed)
    var userFactors = initialize(userInBlocks, rank, seedGen.nextLong())
    var itemFactors = initialize(itemInBlocks, rank, seedGen.nextLong())
    var previousCheckpointFile: Option[String] = None
    val shouldCheckpoint: Int => Boolean = (iter) =>
      sc.checkpointDir.isDefined && checkpointInterval != -1 && (iter % checkpointInterval == 0)
    val deletePreviousCheckpointFile: () => Unit = () =>
      previousCheckpointFile.foreach { file =>
        try {
          val checkpointFile = new Path(file)
          checkpointFile.getFileSystem(sc.hadoopConfiguration).delete(checkpointFile, true)
        } catch {
          case e: IOException =>
            logWarning(s"Cannot delete checkpoint file $file:", e)
        }
      }
      // 隐式偏好
    if (implicitPrefs) {
      for (iter <- 1 to maxIter) {
        userFactors.setName(s"userFactors-$iter").persist(intermediateRDDStorageLevel)
        val previousItemFactors = itemFactors
        itemFactors = computeFactors(userFactors, userOutBlocks, itemInBlocks, rank, regParam,
          userLocalIndexEncoder, implicitPrefs, alpha, solver)
        previousItemFactors.unpersist()
        itemFactors.setName(s"itemFactors-$iter").persist(intermediateRDDStorageLevel)
        val deps = itemFactors.dependencies
        if (shouldCheckpoint(iter)) {
          itemFactors.checkpoint() 
        }
        val previousUserFactors = userFactors
        userFactors = computeFactors(itemFactors, itemOutBlocks, userInBlocks, rank, regParam,
          itemLocalIndexEncoder, implicitPrefs, alpha, solver)
        if (shouldCheckpoint(iter)) {
          ALS.cleanShuffleDependencies(sc, deps)
          deletePreviousCheckpointFile()
          previousCheckpointFile = itemFactors.getCheckpointFile
        }
        previousUserFactors.unpersist()
      }
      // 显示偏好
    } else {
      for (iter <- 0 until maxIter) {
        itemFactors = computeFactors(userFactors, userOutBlocks, itemInBlocks, rank, regParam,
          userLocalIndexEncoder, solver = solver)
        if (shouldCheckpoint(iter)) {
          val deps = itemFactors.dependencies
          itemFactors.checkpoint()
          itemFactors.count() 
          ALS.cleanShuffleDependencies(sc, deps)
          deletePreviousCheckpointFile()
          previousCheckpointFile = itemFactors.getCheckpointFile
        }
        userFactors = computeFactors(itemFactors, itemOutBlocks, userInBlocks, rank, regParam,
          itemLocalIndexEncoder, solver = solver)
      }
    }
    // 生成用户特征矩阵
    val userIdAndFactors = userInBlocks
      .mapValues(_.srcIds)
      .join(userFactors)
      .mapPartitions({ items =>
        items.flatMap { case (_, (ids, factors)) =>
          ids.view.zip(factors)
        }
      }, preservesPartitioning = true)
      .setName("userFactors")
      .persist(finalRDDStorageLevel)
      // 生成商品特征矩阵
    val itemIdAndFactors = itemInBlocks
      .mapValues(_.srcIds)
      .join(itemFactors)
      .mapPartitions({ items =>
        items.flatMap { case (_, (ids, factors)) =>
          ids.view.zip(factors)
        }
      }, preservesPartitioning = true)
      .setName("itemFactors")
      .persist(finalRDDStorageLevel)
    if (finalRDDStorageLevel != StorageLevel.NONE) {
      userIdAndFactors.count()
      itemFactors.unpersist()
      itemIdAndFactors.count()
      userInBlocks.unpersist()
      userOutBlocks.unpersist()
      itemInBlocks.unpersist()
      itemOutBlocks.unpersist()
      blockRatings.unpersist()
    }
    (userIdAndFactors, itemIdAndFactors)
  }

5.2.6.1 computeFactors

我们可以看到，构建最小二乘的方法是在computeFactors方法中实现的。我们以商品inblock信息结合用户outblock信息构建最小二乘为例来说明这个过程:

  private def computeFactors[ID](
      srcFactorBlocks: RDD[(Int, FactorBlock)],
      srcOutBlocks: RDD[(Int, OutBlock)],
      dstInBlocks: RDD[(Int, InBlock[ID])],
      rank: Int,
      regParam: Double,
      srcEncoder: LocalIndexEncoder,
      implicitPrefs: Boolean = false,
      alpha: Double = 1.0,
      solver: LeastSquaresNESolver): RDD[(Int, FactorBlock)] = {
    val numSrcBlocks = srcFactorBlocks.partitions.length
    // 若隐式偏好 
    // 则计算 YtY
    val YtY = if (implicitPrefs) Some(computeYtY(srcFactorBlocks, rank)) else None
    val srcOut =
    // 用用户outblock与userFactor进行join操作 
    srcOutBlocks.join(srcFactorBlocks).flatMap {
      case (srcBlockId, (srcOutBlock, srcFactors)) =>
        srcOutBlock.view.zipWithIndex.map { case (activeIndices, dstBlockId) =>
        // 每一个商品分区包含一组所需的用户分区及其对应的用户factor信息
        // 格式即（商品分区id集合，（用户分区id集合，用户分区对应的factor集合））
          (dstBlockId, (srcBlockId, activeIndices.map(idx => srcFactors(idx))))
        }
    }

    // 以商品分区id为key进行分组
    val merged = srcOut.groupByKey(new ALSPartitioner(dstInBlocks.partitions.length))
    // 用商品inblock信息与merged进行join操作
    dstInBlocks.join(merged).mapValues {
    ......

我们知道求解商品值时，我们需要通过所有和商品关联的用户向量信息来构建最小二乘问题。这里有两个选择，第一是扫一遍InBlock信息，同时对所有的产品构建对应的最小二乘问题； 第二是对于每一个产品，扫描InBlock信息，构建并求解其对应的最小二乘问题。第一种方式复杂度较高，spark选取第二种方法求解最小二乘问题，同时也做了一些优化。 做优化的原因是二种方法针对每个商品，都会扫描一遍InBlock信息，这会浪费较多时间，为此，将InBlock按照商品id进行排序，我们通过一次扫描就可以创建所有的最小二乘问题并求解。 我们来继续看代码：

......
// 遍历各个商品分区
// 数据格式为 （（该商品分区的不重复的有序的商品id集合，该商品分区的商品位置偏移集合，该商品分区中对应的用户id集合，打分集合），（用户分区id集合->用户分区对应的factor集合））
      case (InBlock(dstIds, srcPtrs, srcEncodedIndices, ratings), srcFactors) =>
      // 从 srcFactors: Iterable[(Int,Array[Array[Float]])] 中取出值到数组sortedSrcFactors
      // 即得得到用户特征数组
        val sortedSrcFactors = new Array[FactorBlock](numSrcBlocks)
        srcFactors.foreach { case (srcBlockId, factors) =>
          sortedSrcFactors(srcBlockId) = factors
        }
        // 保存要求解的商品特征
        val dstFactors = new Array[Array[Float]](dstIds.length)
        var j = 0
        // 保存rank维度的正规方程组
        val ls = new NormalEquation(rank)
        // 遍历商品
        while (j < dstIds.length) {
          ls.reset()
          if (implicitPrefs) {
            ls.merge(YtY.get)
          }
          var i = srcPtrs(j)
          var numExplicits = 0
          // 商品dstIds(j)对应的遍历用户
          while (i < srcPtrs(j + 1)) {
          // 解码得到用户分区号 和 该分区内的地址
            val encoded = srcEncodedIndices(i)
            val blockId = srcEncoder.blockId(encoded)
            val localIndex = srcEncoder.localIndex(encoded)
            // 得到 该用户特征向量
            val srcFactor = sortedSrcFactors(blockId)(localIndex)
            val rating = ratings(i)
            if (implicitPrefs) {
              val c1 = alpha * math.abs(rating)
              if (rating > 0) {
                numExplicits += 1
                ls.add(srcFactor, (c1 + 1.0) / c1, c1)
              }
            } else {
              ls.add(srcFactor, rating)
              numExplicits += 1
            }
            i += 1
          }
          // 优化商品dstIds(j)对应的特征向量
          dstFactors(j) = solver.solve(ls, numExplicits * regParam)
          j += 1
        }
        dstFactors
    }
  }

5.2.7 优化器

接下来我们讲讲上一节中对特征向量进行优化的优化器。

  private[recommendation] trait LeastSquaresNESolver extends Serializable {
    def solve(ne: NormalEquation, lambda: Double): Array[Float]
  }

CholeskySolver和NNLSSolver实现了LeastSquaresNESolver。

5.2.7.1 CholeskySolver

  private[recommendation] class CholeskySolver extends LeastSquaresNESolver {

    /**
     * 这里所使用的代价函数为：
     *   $min norm(A x - b)^2^ + lambda * norm(x)^2^$
     */
    override def solve(ne: NormalEquation, lambda: Double): Array[Float] = {
      val k = ne.k
      // 在上正定矩阵A的对角线上加上lambda
      var i = 0
      var j = 2
      while (i < ne.triK) {
        ne.ata(i) += lambda
        i += j
        j += 1
      }
      //直接调用netlib-java封装的方法实现
      CholeskyDecomposition.solve(ne.ata, ne.atb)
      val x = new Array[Float](k)
      i = 0
      while (i < k) {
        x(i) = ne.atb(i).toFloat
        i += 1
      }
      ne.reset()
      x
    }
  }

5.2.7.2 NNLSSolver

  private[recommendation] class NNLSSolver extends LeastSquaresNESolver {
    private var rank: Int = -1
    private var workspace: NNLS.Workspace = _
    private var ata: Array[Double] = _
    private var initialized: Boolean = false

    private def initialize(rank: Int): Unit = {
      if (!initialized) {
        this.rank = rank
        workspace = NNLS.createWorkspace(rank)
        ata = new Array[Double](rank * rank)
        initialized = true
      } else {
        require(this.rank == rank)
      }
    }

    /**
     * Solves a nonnegative least squares problem with L2 regularization:
     *
     *   min_x_  norm(A x - b)^2^ + lambda * n * norm(x)^2^
     *   subject to x >= 0
     */
    override def solve(ne: NormalEquation, lambda: Double): Array[Float] = {
      val rank = ne.k
      initialize(rank)
      fillAtA(ne.ata, lambda)
      val x = NNLS.solve(ata, ne.atb, workspace)
      ne.reset()
      x.map(x => x.toFloat)
    }

    /**
     * Given a triangular matrix in the order of fillXtX above, compute the full symmetric square
     * matrix that it represents, storing it into destMatrix.
     */
    private def fillAtA(triAtA: Array[Double], lambda: Double) {
      var i = 0
      var pos = 0
      var a = 0.0
      while (i < rank) {
        var j = 0
        while (j <= i) {
          a = triAtA(pos)
          ata(i * rank + j) = a
          ata(j * rank + i) = a
          pos += 1
          j += 1
        }
        ata(i * rank + i) += lambda
        i += 1
      }
    }
  }

6. 参考文献

【1】Y Koren, R Bell, C Volinsky. Matrix factorization techniques for recommender systems. IEEE, Computer Journal,2009: 42(8), 30-37
【2】ZHENG F. Matrix factorization recommendation algorithm based on Spark [D]. Chengdu: School of Information Science and Technology, Southwest Jiaotong University, 2015.
【3】Yang Z.The Research of Recommendation System Based on Spark Platform [D].Anhui:University of Science and Technology of China,2015.
【4】M Zaharia，M Chowdhury，T Das，A Dave，J Ma . Resilient Distributed Datasets: A Fault-Tolerant Abstraction for In-Memory Cluster Computing. Usenix Conference on Networked Systems Design, 2012, 70(2):141-146
【5】《交换最小二乘》