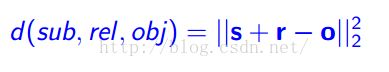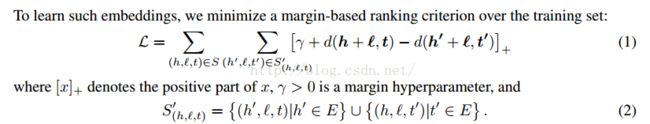TransE算法(Translating Embedding)
http://blog.csdn.net/u011274209/article/details/50991385
一、引言
网络上已经存在了大量知识库(KBs),比如OpenCyc,WordNet,Freebase,Dbpedia等等。这些知识库是为了各种各样的目的建立的,因此很难用到其他系统上面。为了发挥知识库的图(graph)性,也为了得到统计学习(包括机器学习和深度学习)的优势,我们需要将知识库嵌入(embedding)到一个低维空间里(比如10、20、50维)。我们都知道,获得了向量后,就可以运用各种数学工具进行分析。深度学习的输入也是向量。(考虑一下,word2vec,我们训练出一个向量后,可以做好多事情,深度学习的输入也往往是一个矩阵。另可见:词嵌入的类比特性有实用意义吗?)。
二、基础背景
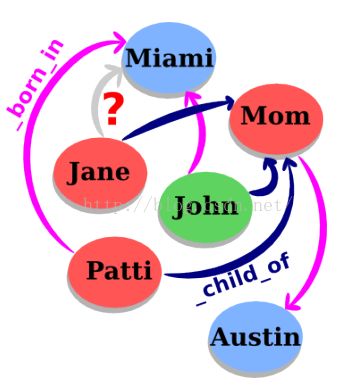
一条知识图谱可以表示为一个三元组(sub,rel,obj)。举个例子:小明的爸爸是大明,表示成三元组是(小明,爸爸,大明)。前者是主体,中间是关系,后者是客体。主体和客体统称为实体(entity)。关系有一个属性,不可逆,也就是说主体和客体不能颠倒过来。
知识图谱的集合,链接起来成为一个图(graph),每个节点是一个一个实体,每条边是一个关系,或者说是一个事实(fact)。也就是有向图,主体指向客体。
具体的用处和知识图谱提取方式可见刘知远大神的文章http://www.36dsj.com/archives/31317(ps,最好是买本他的书)
Freebase的例子:
上面三条都是知识图谱的例子。
三、TransE的提出
TranE是一篇Bordes等人2013年发表在NIPS上的文章提出的算法。它的提出,是为了解决多关系数据(multi-relational data)的处理问题。我们现在有很多很多的知识库数据knowledge bases (KBs),比如Freebase、 Google Knowledge Graph 、 GeneOntology等等。
TransE的直观含义,就是TransE基于实体和关系的分布式向量表示,将每个三元组实例(head,relation,tail)中的关系relation看做从实体head到实体tail的翻译(其实我一直很纳闷为什么叫做translating,其实就是向量相加),通过不断调整h、r和t(head、relation和tail的向量),使(h + r) 尽可能与 t 相等,即 h + r = t。
以前有很多种训练三元组的方法,但是参数过多,以至于模型过于复杂难以理解(作者表达的意思就是,我们的工作效果和你们一样,但我们的简单易扩展)。(ps:作者以前也做过类似的工作,叫做Structured Embeddings,简称SE,只是将实体转为向量,关系是一个矩阵,利用矩阵的不可逆性反映关系的不可逆性。距离表达公式是1-norm)。
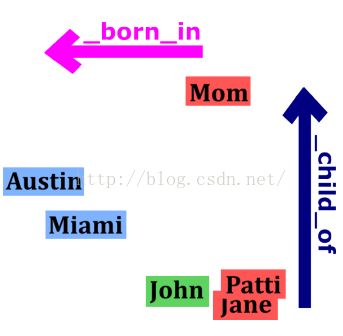
如下图,作者的目的是将向量转为这种形式(此图是2维)
为此,作者定义了距离公式为
四、TransE的训练
注释:
1、
直观上,我们要前面的项(原三元组)变小(positive),后面的项(打碎的三元组)变大(negative)。就跟喂小狗一样,它做对了,就给骨头吃;做错了,就打两下。前面的项是对的(来自于训练集),后面的项是错的(我们随机生成的)。不同时打碎主体和客体,随机挑选一个打碎,另一个保持不变,这样才能够有对照性。
2、图上的加号是大于0取原值,小于0则为0。我们叫做合页损失函数(hinge loss function),这种训练方法叫做margin-based ranking criterion。是不是听起来很熟悉?对的,就是来自SVM。支持向量机也是如此,要将正和负尽可能分开,找出最大距离的支持向量。同理,TransE也是如此,我们尽可能将对的和错的分开。margin值一般设为1了。
3、关于模型的参数:参数θ是所有实体的向量。设一共有 |E| 个实体和 |R| 个关系,每个实体/关系的向量长度为d维,因此,一共有( |E| + |R| ) * d 个参数。
4、关于参数的更新:我们使用的是随机梯度下降(Stochastic Gradient Descent,SGD)训练方法。SGD不用对所有的和求梯度,而是对一个batch求梯度之后就立即更新theta值。
对于数据集大的情况下,有速度。但是每一次更新都是针对这一个batch里的三元组的向量更新的,也就是意味着,一次更新最多更新(3+2)*batch_size*d 个参数(设一个batch的长度为batch_size)。并不是把所有的theta值都更新了,或者说不用更新整个( |E| + |R| ) * d 矩阵,只需要更新sample里抽出来的batch里的向量即可。为什么可以这样呢(也就是为什么可以不用把参数全更新了,而是只更新一部分)?因为参数之间并没有依赖(或者说冲突conflict),对于此,可以参考论文 Hogwild!: A Lock-Free Approach to Parallelizing Stochastic。
5、对SGD多说两句:SGD的收敛没有GD好,但是,这反而是优点,因为在机器学习领域,过于best的结果反而是害处,因为用于过拟合(overfitting)。也就是,尽管叫做D(下降),但整个过程我们难保一直D下去。只能保证在forever可以做到D。
6、归一化公式的分母是向量的平方和再开方;而对于距离公式,是向量的平方和(没有开方)。公式的错误书写,会引起收敛的失败。
7、对于每一次迭代,每一次的归一化约束(constraint)实体长度为1(减少任意度量(scaling freedoms(SE)),使得收敛有效(避免 trivially minimize(transE)),但对关系不做此要求。(然而我自己试验的结果是,归一化关系,会使精度加大和收敛加强)
tranE的python代码(github)