java并行流
在java7之前,处理并行数据非常麻烦. 第一:你得明确的把包含的数据结构分成若干子部分. 第二:你要给每个子部分分配独立的线程. 第三:你需要在恰当的时候对他们进行同步,来避免不希望出现的竞争条件,等待所有线程完成,最后把这些结果合并起来.
在前面的文章中,我们介绍了 Stream接口,让你可以很方便的处理它的元素,可以调用ParallelStream 方法把集合转换成并行流.
并行流就是把一个内容分成多个数据块,并用不同线程分别处理每个数据块的流.
这样一来,你就可以把给定的工作负荷自动分配给多个处理器内核,让他们都忙起来.
假设你需要写一个方法,接受数字n作为参数,并返回从1到给定参数的所有数字的和。一个 直接(也许有点土)的方法是生成一个无穷大的数字流,把它限制到给定的数目,然后用对两个 数字求和的 BinaryOperator 来归约这个流,如下所示:
//顺序
public static Long sequentialSum(Long n){
return Stream.iterate(1L, i->i+1L)
.limit(n)
.reduce(0L,Long::sum);
}
用更为传统的Java术语来说,这段代码与下面的迭代等价
//传统迭代
public static Long iterativeSum(Long n){
Long result = 0L;
for (Long i=1L;i这似乎是利用并行流的好机会,特别是n很大的时候,那该怎样做呢?
你要对结果变量进行同步吗?用多少个线程呢?谁负责生成数呢?谁来做加法呢?
其实根本不必担心,并行流已经帮我们做完了这些令人头疼的工作
将顺序流转换为并行流
//并行流
public static Long parallelSum(Long n){
return Stream.iterate(1L,i->i+1L)
.limit(n)
.parallel()
.reduce(0L,Long::sum);
}
在现实中,对顺序流调用 parallel 方法并不意味着流本身有任何实际的变化。它 在内部实际上就是设了一个 boolean 标志,表示你想让调用 parallel 之后进行的所有操作都并 行执行.类似地,你只需要对并行流调用 sequential 方法就可以把它变成顺序流.
测量流性能
我们说并行求和的方法应该比顺序迭代的方法更好.但在软件工程上, 靠猜绝对不是什么好办法,有时候经验也靠不住. 你应该始终遵循三个黄金规则;测量,测量,再测量.
为了简化测量,我们写个方法,专门用来测试 ParallelStreams类里的三个求和方法: sequentialSum iterativeSum, parallelSum.
public Long measureSumPref(Function addr, Long n) {
long fastest = Long.MAX_VALUE;
for (int i = 0; i < 10; i++) {
Long start = System.nanoTime();
Long sum = addr.apply(n);
Long druation = (System.nanoTime() - start)/1000000;
if (druation < fastest) {
fastest = druation;
}
}
return fastest;
}
这个方法会接收一个函数和一个Long类型参数.它会对传给方法的参数应用函数10次,记录每次执行的时间.
下面是测试结果
//顺序
@Test
public void test4() {
Long fast = measureSumPref(ParallelStreams::sequentialSum, 1000 * 10000L);
System.out.println("sequentialSum= " + fast);//398毫秒
}
//迭代
@Test
public void test5() {
Long fast = measureSumPref(ParallelStreams::iterativeSum, 1000 * 10000L);
System.out.println("iterativeSum= "+ fast);//153毫秒
}
//并行
@Test
public void test6(){
Long fast = measureSumPref(ParallelStreams::parallelSum, 1000 * 10000L);
System.out.println("parallelSum= "+fast);//1309毫秒
}
看到结果,我们发现并行流操作相当令我们失望.
求和方法的并行版本比顺序版本要慢很多!!! 其实对这个意外的结果,有两方面的原因:
-
一:iterate 生成的是装箱对象,必须拆箱成数字才能求和.
-
二:我们很难把iterate分成多个独立的块来执行.
对于第二个问题,很有意思,我们直觉上可能是这样运行的,如图:
但是,iterate 很难分割成能够独立执行的小块,因为每次应用这个函数都要依赖前一次应用的结果
也就是说,整张数字表在归纳过程开始时还没准备好,因为Stream在遇到终端操作才会开始执行,因而无法有效的把流划分为小块进行处理. 把流标记为并行,其实是给顺序处理增加了开销,它还要把每次求和操作的结果分到一个不同的线程上.
这就说明了并行编程肯能很复杂,如果用得不对(比如采用了一个不易并行化的操作,如 iterate ),它甚至可能让程序的整体性能更差. 所以在调用那个看似神奇的 parallel 操作时,了解背后到底发生了什么是很有必要的。
并行流使用注意事项:使用更有针对性的方法
对于上面那种出人意料的结果,我们万不可把锅退给并行流,其实仔细分析,不难发现,这是我们使用了不恰当的的数据结构导致的.
对于上面的并行处理操作,我们可做如下改进.在之前的文章中,我们介绍过一个叫LongStream的流.这个流有个专门针对Long型的方法
- LongStream.rangeClosed 直接产生原始类型的long数字,没有装箱拆箱的开销.
- LongStream.rangeClosed 会生成数字范围,很容易查分为独立的小块.
LongStream和Stream一样都继承了BaseStream
public interface LongStream extends BaseStream {...}
public interface Stream extends BaseStream> {...}
这两个流的用法基本完全相同,唯一的不同相比从名字就能看出来,LongStream 指明了流类型为Long,类似的还有,IntStream,DoubleStream等
我们改进代码如下:
//顺序流改进版 LongStream.rangeClosed
public static Long sequentialSum2(Long n) {
return LongStream.rangeClosed(1, n)
.reduce(0L,Long::sum);
}
//并行流改进版
public static Long paraparallelSum2(Long n) {
return LongStream.rangeClosed(1, n)
.parallel()
.reduce(0L,Long::sum);
}
然后再次进行测量
//顺序流(改进版)
@Test
public void test7(){
Long fast = measureSumPref(ParallelStreams::sequentialSum2, 1000 * 10000L);
System.out.println("顺序流(改进版)="+fast);//56毫秒------改进之前:398毫秒
}
//并行流(改进版)
@Test
public void test8(){
Long fast = measureSumPref(ParallelStreams::paraparallelSum2, 1000 * 10000L);
System.out.println("并行流(改进版)="+fast);//14毫秒--------改进之前:1309毫秒
}
由此结果可得出结论:
-
使用LongStream比iterate效率提高 710%
-
在上面基础上使用 并行流 比 顺序流 效率提高 400%
可见:选择适当的数据结构往往比并行算法正重要,使用正确的数据结构后再选择并行算法能保证最佳的性能.
尽管如此,我们也必须知道,并行化不是没有代价的.并行化本身需要对流做递归划分,把每个子流的归纳操作分配到不同的线程,然后把这些操作的结果合并成一个值.
但在多个内核之间移动数据的代价也可能比你想的要大,所以在使用并行操作很重要的一点就是要保证并行执行的工作时间要比数据在内核之前移动的时间要长.
在使用并行Stream加速代码之前,你必须确保用的对,如果用错了,算得快就毫无意义了.让我们看一个常见的陷阱.
高效使用并行流
如果有疑问,测量。把顺序流转成并行流轻而易举,但却不一定是好事
-
留意装箱。自动装箱和拆箱操作会大大降低性能。Java 8中有原始类型流( IntStream 、 LongStream 、 DoubleStream )来避免这种操作,但凡有可能都应该用这些流
-
有些操作本身在并行流上的性能就比顺序流差。特别是 limit 和 findFirst 等依赖于元 素顺序的操作,它们在并行流上执行的代价非常大。例如, findAny 会比 findFirst 性 能好,因为它不一定要按顺序来执行。
-
还要考虑流的操作流水线的总计算成本。设N是要处理的元素的总数,Q是一个元素通过 流水线的大致处理成本,则N*Q就是这个对成本的一个粗略的定性估计。Q值较高就意味 着使用并行流时性能好的可能性比较大。
-
对于较小的数据量,选择并行流几乎从来都不是一个好的决定。并行处理少数几个元素 的好处还抵不上并行化造成的额外开销
-
要考虑流背后的数据结构是否易于分解。例如, ArrayList 的拆分效率比 LinkedList 高得多,因为前者用不着遍历就可以平均拆分,而后者则必须遍历
-
还要考虑终端操作中合并步骤的代价是大是小(例如 Collector 中的 combiner 方法)
需要强调的是:并行流背后使用的基础架构是java7引入的分支/合并框架.我们想要正确高效的使用并行流,了解它的内部原理至关重要.
分支/合并框架详解
分支框架的目的是以递归的方式将可以并行的任务拆分成更小的任务,然后将每个子任务的结果合并起来生成整体结果.
它是 ExecutorService 接口的一个实现,他把子任务分配给线程池(ForkJoinPool)中的线程.
使用 RecursiveTask
要把任务提交到池,必须创建 RecursiveTask 的一个子类,其中V是并行化任务产生的结果类型,
RecursiveTask类源码:
public abstract class RecursiveTask extends ForkJoinTask {
private static final long serialVersionUID = 5232453952276485270L;
/**
* The result of the computation.
*/
V result;
/**
* The main computation performed by this task.
* @return the result of the computation
*/
protected abstract V compute();
public final V getRawResult() {
return result;
}
protected final void setRawResult(V value) {
result = value;
}
/**
* Implements execution conventions for RecursiveTask.
*/
protected final boolean exec() {
result = compute();
return true;
}
}
要定义 RecursiveTask, 只需实现它唯一的抽象方法compute :
@Override
protected Long compute() {
return null;
}
这个方法定义了将任务拆分成子任务的逻辑,以及无法再拆分或不便再拆分,生成单个子任务结果的逻辑.
即(伪代码如下):
if (任务足够小或不可分) {
顺序计算该任务
} else {
将任务分成两个子任务
递归调用本方法,拆分每个子任务,等待所有子任务完成
合并每个子任务的结果
}
如果你了解著名的分治算法,会发现这不过是分支算法的并行版本而已.
接下来我们举一个用分支/合并框架的实际例子,还以前面的例子为基础,让我们试着用这个框架为一个数字范围(这里用一个long[] 数组表示)求和
/**
* 分支合并框架测试
*
* @author itguang
* @create 2017-11-18 14:22
**/
public class ForkJoinTest extends RecursiveTask {
//要处理的任务数组
private final long[] numbers;
//子任务处理数组的起始和结束位置
private final int start;
private final int end;
//阀值,当数组小于10000就并行执行
public static final long THRESHOLD = 10000;
//公共构造函数,用于创建子任务
//私有构造函数,用于 以递归方式为主任务创建子任务
public ForkJoinTest(long[] numbers, int start, int end) {
this.numbers = numbers;
this.start = start;
this.end = end;
}
public ForkJoinTest(long[] numbers) {
this(numbers, 0, numbers.length);
}
@Override
protected Long compute() {
int length = end - start;
//如果大小小于等于阀值,则顺序计算结果
if (length <= THRESHOLD) {
return computeSequentially();
}
//否则,创建一个子任务为数组的前一半求和
ForkJoinTest leftTask = new ForkJoinTest(numbers, start, start + length / 2);
//利用另一个 ForkJoinPool 里的线程异步执行新创建的子任务.
leftTask.fork();//对子任务调用 fork 方法可以把它排进 ForkJoinPool 。
//创建一个任务为数组的后一半求和
ForkJoinTest rightTask = new ForkJoinTest(numbers, start + length / 2, end);
//**递归操作**
long rightResult = rightTask.compute();
//遇到递归终止条件,读取本次递归第一个子任务的结果,如果尚未完成就等待
long leftResult = leftTask.join();
//递归累加
return leftResult+rightResult;
}
//计算和
private long computeSequentially() {
long sum = 0;
for (int i = start; i < end; i++) {
sum += numbers[i];
}
return sum;
}
}
测试:创建一个 ForkJoinPool,并把任务传递给它的invoke()方法.在ForkPool中执行时,返回结果就是ForkJoinTest的并行递归求和结果
@Test
public void test9(){
long[] numbers = LongStream.rangeClosed(1, 1000*10000).toArray();
ForkJoinTest forkJoinTest = new ForkJoinTest(numbers);
Long sum = new ForkJoinPool().invoke(forkJoinTest);
System.out.println(sum);//50000005000000
}
请注意在实际应用时,使用多个 ForkJoinPool 是没有什么意义的。正是出于这个原因,一 般来说把它实例化一次,然后把实例保存在静态字段中,使之成为单例,这样就可以在软件中任 何部分方便地重用了。这里创建时用了其默认的无参数构造函数,这意味着想让线程池使用JVM 能够使用的所有处理器。更确切地说,该构造函数将使用 Runtime.availableProcessors 的 返回值来决定线程池使用的线程数。请注意 availableProcessors 方法虽然看起来是处理器, 但它实际上返回的是可用内核的数量,包括超线程生成的虚拟内核。
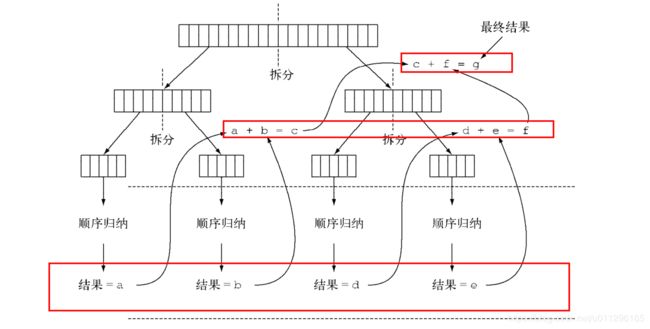
当把一个ForkJoinTask 任务交给ForkJoinPool时,这个任务就由池中的一个线程执行,这个线程会调用任务的 compute 方法. 该方法会检查任务是否小到足以顺序执行,如果不够小则会把要求和的数组分成两半,分给两个新的 ForkJoinTest ,而它们也由ForkJoinPool 安排执行.
因此这一过程可以递归重复,把原任务拆分成更小的任务执行,知道满足不可拆分的条件,在上例中是拆分数组的大小小于阀值. 这时候会从递归终止开始顺序计算每个任务的结果.然后由分支创建的二叉树遍历回它的根.接下来会合并每个子任务的部分结果,从而得到总任务的结果.
如图:
使用分支/合并框架的最佳做法
-
对一个任务调用 join 方法会阻塞调用方,直到该任务做出结果。因此,有必要在两个子 任务的计算都开始之后再调用它。否则,你得到的版本会比原始的顺序算法更慢更复杂, 因为每个子任务都必须等待另一个子任务完成才能启动。
-
不应该在 RecursiveTask 内部使用 ForkJoinPool 的 invoke 方法。相反,你应该始终直 接调用 compute 或 fork 方法,只有顺序代码才应该用 invoke 来启动并行计算。
-
对子任务调用 fork 方法可以把它排进 ForkJoinPool 。同时对左边和右边的子任务调用 它似乎很自然,但这样做的效率要比直接对其中一个调用 compute 低。这样做你可以为 其中一个子任务重用同一线程,从而避免在线程池中多分配一个任务造成的开销
-
和并行流一样,你不应理所当然地认为在多核处理器上使用分支/合并框架就比顺序计 算快。我们已经说过,一个任务可以分解成多个独立的子任务,才能让性能在并行化时 有所提升。所有这些子任务的运行时间都应该比分出新任务所花的时间长;一个惯用方 法是把输入/输出放在一个子任务里,计算放在另一个里,这样计算就可以和输入/输出 同时进行。此外,在比较同一算法的顺序和并行版本的性能时还有别的因素要考虑。就 像任何其他Java代码一样,分支/合并框架需要“预热”或者说要执行几遍才会被JIT编 译器优化。这就是为什么在测量性能之前跑几遍程序很重要,我们的测试框架就是这么 做的。同时还要知道,编译器内置的优化可能会为顺序版本带来一些优势(例如执行死 码分析——删去从未被使用的计算)。
ForkJoinTask工作窃取算法
在 ForkJoinSumCalculator 的例子中,我们决定在要求和的数组中最多包含10 000个项目 时就不再创建子任务了。这个选择是很随意的,但大多数情况下也很难找到一个好的启发式方法 来确定它,只能试几个不同的值来尝试优化它。在我们的测试案例中,我们先用了一个有1000 万项目的数组,意味着 ForkJoinSumCalculator 至少会分出1000个子任务来。这似乎有点浪费 资源,因为我们用来运行它的机器上只有四个内核。在这个特定例子中可能确实是这样,因为所 有的任务都受CPU约束,预计所花的时间也差不多。
但分出大量的小任务一般来说都是一个好的选择。这是因为,理想情况下,划分并行任务时, 应该让每个任务都用完全相同的时间完成,让所有的CPU内核都同样繁忙。不幸的是,实际中,每 个子任务所花的时间可能天差地别,要么是因为划分策略效率低,要么是有不可预知的原因,比如 磁盘访问慢,或是需要和外部服务协调执行。
分支/合并框架工程用一种称为工作窃取(work stealing)的技术来解决这个问题。在实际应 用中,这意味着这些任务差不多被平均分配到 ForkJoinPool 中的所有线程上。每个线程都为分 配给它的任务保存一个双向链式队列,每完成一个任务,就会从队列头上取出下一个任务开始执 行。基于前面所述的原因,某个线程可能早早完成了分配给它的所有任务,也就是它的队列已经 空了,而其他的线程还很忙。这时,这个线程并没有闲下来,而是随机选了一个别的线程,从队 列的尾巴上“偷走”一个任务。这个过程一直继续下去,直到所有的任务都执行完毕,所有的队 列都清空。这就是为什么要划成许多小任务而不是少数几个大任务,这有助于更好地在工作线程 之间平衡负载。
一般来说,这种工作窃取算法用于在池中的工作线程之间重新分配和平衡任务。如图展示 了这个过程。当工作线程队列中有一个任务被分成两个子任务时,一个子任务就被闲置的工作线 程“偷走”了。如前所述,这个过程可以不断递归,直到规定子任务应顺序执行的条件为真。
小结:
-
内部迭代让你可以并行处理一个流,而无需在代码中显式使用和协调不同的线程。
-
虽然并行处理一个流很容易,却不能保证程序在所有情况下都运行得更快。并行软件的 行为和性能有时是违反直觉的,因此一定要测量,确保你并没有把程序拖得更慢。
-
从性能角度来看,使用正确的数据结构,如尽可能利用原始流而不是一般化的流,几乎 总是比尝试并行化某些操作更为重要
-
分支/合并框架让你得以用递归方式将可以并行的任务拆分成更小的任务,在不同的线程 上执行,然后将各个子任务的结果合并起来生成整体结果
-
Spliterator 定义了并行流如何拆分它要遍历的数据。
引用 《java8实战》 github