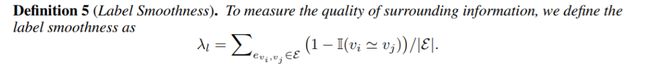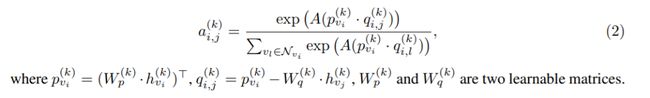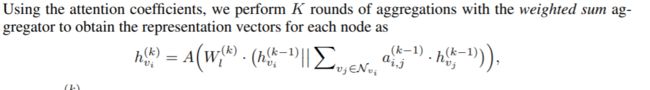ICLR2020 | CS-GNN:用平滑度刻画图信息的使用
作者 | 李梓盟
审稿 | 俞琳荟
今天给大家介绍香港中文大学和新加坡国立大学一起在ICLR2020上发布的一篇论文,该论文针对实际使用中GNN在图结构数据中能够获得多少性能的问题,提出了两种可以度量从图中获取的信息的数量和质量的平滑度指标,以及一个使用上述平滑度指标的GNN框架CS-GNN。实验显示,在不同类型的图上,对于特定任务而言,CS-GNN相比于现有的模型有更好的效果。
1
简介
图是很重要的数据结构,它可以准确表达对象(节点)之间的各种关系(边)。近些年来,国内外研究人员对GNN在诸如节点分类和边预测之类的任务上进行了广泛的研究。长期的研究显示,GNN通过利用图结构数据中的关系信息,在基准数据集上实现了对传统方法的改进。它所产生的突破性结果促使人们在探索例如计算机视觉,自然语言处理,化学,生物学和社交网络等不同领域时广泛使用GNN及其衍生模型。
本文作者主要做出了两个贡献:(1)提出两个图平滑度度量标准,用于帮助理解GNN中图信息的使用;(2)提出一种新的GNN模型,,该模型可以使用平滑度值来改善对图信息的使用。
作者认为GNN之所以优于现有的基于欧几里得(Euclidean)的方法,其主要原因之一是因为GNN可以获得来自对象邻域的丰富信息。GNN通过例如均值、求和、注意力等聚合器收集邻域信息,然后将聚合的特征向量和节点本身的特征向量合并为一个新的特征向量。经过多轮聚合后,节点的特征向量可用于诸如节点分类之类的任务。因此,图结构数据带来的性能提高与邻域信息的数量和质量有很大关系。为此,作者提出了两个关于节点特征和标签的平滑度度量,用来测量节点邻域信息的数量和质量。
作者还认为在实际任务中并非节点的所有邻居都包含相关信息,在给定任务中,邻居节点提供相关信息的同时也会提供相关干扰,简单地使用聚合器聚合邻居节点的特征向量常常不能达到最佳性能。为了解决这个问题,作者提出了一个新模型CS-GNN,该模型使用平滑度指标,选择性地聚合邻域信息,可以有效地放大有用信息并减少负面信息干扰。
2
方法与模型
作者提出了两个图平滑度度量标准,分别为特征平滑度和标签平滑度。其中特征平滑度用于描述信息的数量,特征平滑度越大意味着周围环境可以提供的信息越多。标签平滑度用于描述信息的质量,标签平滑度越小意味着积极信息越多,干扰越少。
2.1 特征平滑度
根据图1特征平滑度定义,较大的λf表示图的特征信号具有较高的频率,这意味着图中的两个连通的节点v和v‘的特征向量xv和xv’有很大可能不相似,换句话说,较大的λf意味着具有不同特征的节点更倾向于连接在一起。作者认为对于具有较高频率特征集的图,目标节点可以从其周围获得更多的信息。
图1 特征平滑度定义
为了证明λf与从周围环境中获得的信息之间的关系,作者提出了相关定理并进行了证明,图2为作者提出的相关定理。作者提出较大的λf表示GNN模型可以从图形数据中获取更多信息。这里的DKL(S || C)在使用平均聚合器时产生的,作者表示即使特征平滑度λf是常数,其他聚合器(例如池化和权重)也可能具有不同的DKL(S || C)值。
图2 相关定理
2.2 标签平滑度
根据图3标签平滑度定义,,较大的λl意味着具有不同标签的节点倾向于连接在一起,在这种情况下,周围环境对该任务产生了更大的负面干扰。作者认为较小的λl意味着节点可以从其周围获得更多积极信息。在使用λl来度量周围信息时,需要有标签的数据进行训练,当一些图结构数据没有很多有标签节点的时候,作者提出使用标记数据的子集来估计λl,这也可以获得良好的结果。
图3 标签平滑度定义
2.3 CS-GNN
本文中作者所提出的CS-GNN使用加权和聚合器,合并函数为连接。为了计算每K轮的系数,作者采用了乘法注意力机制,通过将邻居节点的特征向量与节点的自身特征向量相乘来获得注意力系数,并应用softmax函数进行归一化,第k轮中的每个系数a(k)i,j定义如图4所示:
图4 第k轮中的每个系数a(k)i,j定义
为了提高对周围信息的利用,作者在CS-GNN使用了特征平滑度和标签平滑度来控制周围信息的使用,具体使用方法如下:(1)使用λl(标签平滑度)来丢弃带有负面信息的邻居节点,即如果a(k)i,j小于第r个最小注意力系数的值,则将a(k)i,j置为0,这样可以去除这些邻居节点的干扰,保留节点自身的功能。(2)使用λf(特征平滑度)来估计获取信息的数量,并用它来设置上下文向量的维度。较大的尺寸会引起注意力机制的波动,而较小的尺寸会限制其表达力,因此设置适当的尺寸可以获得较好的性能。(3)使用了和GAT不同的注意力系数表示方法,作者使用了q(k)i,j,即节点vi与邻居vj的特征向量之差。之所以使用q(k)i,j,作者表示较大的λf表示节点及其邻居的特征更不相似,这意味着邻居可以贡献更多的信息。因此,通过使用q(k)i,j,当节点vi及其相邻节点vj的特征较为不相似/相似时,我们可以获得更大/更小的a(k)i,j,图5为使用加权和聚合器执行K轮聚合时,节点a的表示向量。
图5 第k轮节点a的特征向量
现实世界的图通常包含一些辅助信息,例如节点和边的属性,局部拓扑特征和边方向等。作者提到CS-GNN可以包含丰富的辅助信息,并使用这些信息来提高性能。作者以局部拓扑特征为例,在注意力机制中,获得局部拓扑特征后将它纳入到节点特征信息中,从而将其视为节点特征信息的一部分,图6为将局部拓扑特征tvi纳入到节点特征信息公式,图7为在全连接层中使用局部拓扑特征tvi获得预测标签公式
图6 节点使用局部拓扑特征tvi
图7 预测标签使用局部拓扑特征tvi
3
实验
作者的实验分为二部分,第一部分先比较了CS-GNN和经典模型在节点分类任务上的效果,第二部分评估了不同特征平滑度和标签平滑度对基于神经网络的方法在给定任务上性能的影响。
作者采用了三种类型的方法作比较,分别为基于拓扑的方法,基于特征的方法和GNN方法,每种方法选择了几种代表性模型,基于拓扑的方法选用了struc2vec (Ribeiro et al., 2017), GraphWave (Donnat et al., 2018) 和Label Propagation (Zhu & Ghahramani, 2002),基于特征的方法选用了LogisticRegression 和MLP(Multilayer Perceptron),GNN方法则选用了GCN,GraphSAGE和GAT。
作者采用了五个现实世界的数据集作为实验数据集,包括Citeseer, Cora,PubMed三个引用网络,一个亚马逊的计算机联合采购网络和一个边界网关协议(BGP)网络。作者将数据集的70%用于训练,10%用于验证,20%用于测试,使用F1-Micro分数来衡量每种方法的节点分类性能,并对所有模型使用默认参数或与CS-GNN相同的参数。
表1 平滑度值
表1报告了每个数据集的两个平滑度值。Amazon的λf值比其余的要大得多,而PubMed的λf值最小,这意味着Amazon中大多数节点的特征向量是不相似的,而对于PubMed而言则相反。对于标签平滑度λl,BGP(small)的值比其他数据集要大得多,这意味着大多数连接节点具有不同的标签。由于BGP(完整)包含许多未标记的节点,因此作者使用BGP(small)的λl作为估算值。
表2 节点分类结果
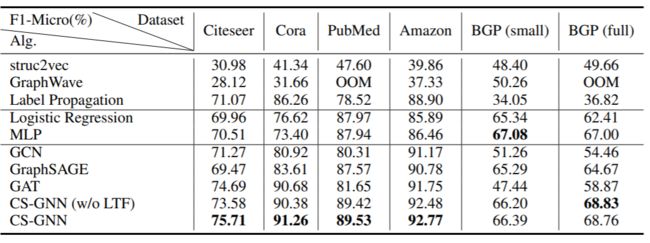
表二显示了不同的模型在五种数据集上的节点分类效果,从分类结果数据上看基于拓扑的方法Label Propagation在引用网络和Amazon网络有很好的表现,作者认为原因是Label Propagation在社区检测上有较好效果,而从图的较小λl值推断出这些图包含许多社区结构,即较小的λl意味着许多节点与其邻居具有相同的类别标签,而连接在一起并且属于同一类别的节点往往会形成一个社区。而对于BGP数据集而言,struc2vec和GraphWave则有更好的表现。对于基于特征的方法,Logistic Regression and MLP在五种数据集上均有相差不大的不错表现。
对于GNN方法而言,除了PubMed和BGP,GCN和GraphSAGE在其他数据集上均有相同的表现,GAT和CS-GNN也有相似效果。作者认为造成这些结果的主要原因是PubMed数据集的λf较小,这意味着节点从周围环境获取的信息较少,而BGP的λl较大,这意味着节点从周围环境获取的大多数信息是负面干扰 在这样的情况下,GraphSAGE和CS-GNN因为使用连接为合并函数从而保留节点自己的特征,因此在PubMed和BGP上相比于其他模型效果更好。而对于其他数据集,GAT和CS-GNN的F1-Micro得分比所有其他模型都高得多。总体而言,作者认为CS-GNN是在所有数据集上都具有较好表现的模型。
为了更好的验证平滑度对实验结果的影响,减少其他因素的干扰,作者通过在Amazon单一数据集上进行实验的方法来验证平滑度的影响。为了改变平滑度,作者对二种平滑度分别进行了相应操作:(1)为了改变λf,作者将节点的特征向量广播到其邻居,当节点接收到特征向量时,它会将其当前特征向量和接收到的那些特征向量的平均值作为新的特征向量,然后再将新的特征向量广播到其邻居。这样一直迭代下去,节点特征会收敛到相同的值,λf的值会逐渐减小(2)为了调整λl,作者随机丢弃连接两个具有不同标签的节点的一部分边,去除这些边会降低λl的值,节点可以从其相邻节点获得更多的正面信息。
图8为平滑度的影响,从图中可以看到随着广播轮数的增加,λf的值相应的减少,GNN模型的效果也随之下降。相反,当λl的值下降时,GNN模型的效果都随之提高。总的来说,GNN模型能够在图结构数据有较大的λf和较小的λl时从周围节点获得更多的正面信息,从而在节点分类等任务上有很好的表现。
图8 平滑度的影响
4
总结
在这篇文章中,作者研究了如何测量GNN从图中获取信息的数量和质量,并提出了特征平滑度和标签平滑度二种平滑度指标。然后,作者还提出了CS-GNN模型,用于应用上述平滑度指标来改善对图信息的使用。通过多个数据集以及多个模型在给定任务上性能的比较,实验结果证明CS-GNN相比于现有模型能够获得更多有用信息,在给定任务上的实验效果优于其他模型。
参考资料
https://iclr.cc/virtual_2020/poster_rkeIIkHKvS.html