语义分割代码阅读---评价指标mIoU的计算

 

1. 语义分割IoU的定义

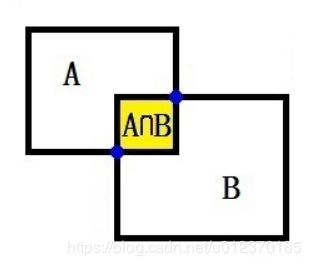
传统意义上的IoU(Intersection over Union，交并比)

直观表示:

公式:    

语义分割中的IoU

在语义分割的问题中，这两个集合为真实值（ground truth）和预测值（predicted segmentation）。
这个比例可以变形为正真数（intersection）比上真正、假负、假正（并集）之和。在每个类上计算IoU，之后平均。

语义分割中的MIoU

Mean Intersection over Union(MIoU，均交并比)：为语义分割的标准度量。其计算所有类别交集和并集之比的平均值.

 

2. 某个类别的IoU的计算

对于pascal数据集来说, 对于21个类别, 分别求IOU:
    对于某一个类别的IOU计算公式如下:

直观理解:

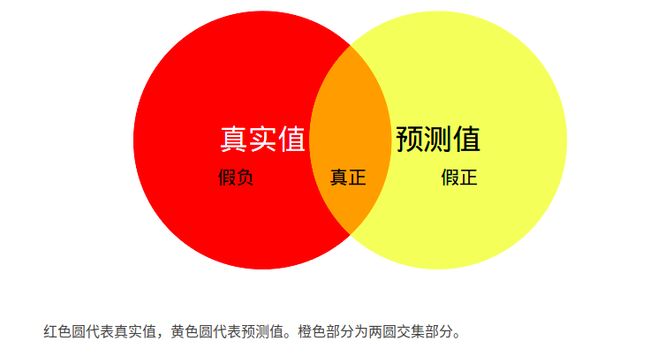
MIoU：计算两圆交集（橙色部分）与两圆并集（红色+橙色+黄色）之间的比例，理想情况下两圆重合，比例为1。

扩展提示:
        TP(真正): 预测正确, 预测结果是正类, 真实是正类 
        FP(假正): 预测错误, 预测结果是正类, 真实是负类
        FN(假负): 预测错误, 预测结果是负类, 真实是正类

        TN(真负): 预测正确, 预测结果是负类, 真实是负类   #跟类别1无关,所以不包含在并集中
        (本例中, 正类:是类别1, 负类:不是类别1)

扩展阅读:

准确率和召回率

3. mIoU的计算

    对于每个类别计算出的IoU求和取平均

步骤一 先求出混淆矩阵

步骤二 再求MIoU

混淆矩阵的每一行再加上每一列，最后减去对角线上的值

import numpy as np

class IOUMetric:
    """
    Class to calculate mean-iou using fast_hist method
    """

    def __init__(self, num_classes):
        self.num_classes = num_classes
        self.hist = np.zeros((num_classes, num_classes))

    def _fast_hist(self, label_pred, label_true):
        # 找出标签中需要计算的类别,去掉了背景
        mask = (label_true >= 0) & (label_true < self.num_classes)
        # # np.bincount计算了从0到n**2-1这n**2个数中每个数出现的次数，返回值形状(n, n)
        hist = np.bincount(
            self.num_classes * label_true[mask].astype(int) +
            label_pred[mask], minlength=self.num_classes ** 2).reshape(self.num_classes, self.num_classes)
        return hist

    # 输入：预测值和真实值
    # 语义分割的任务是为每个像素点分配一个label
    def ev aluate(self, predictions, gts):
        for lp, lt in zip(predictions, gts):
            assert len(lp.flatten()) == len(lt.flatten())
            self.hist += self._fast_hist(lp.flatten(), lt.flatten())
            
        # miou
        iou = np.diag(self.hist) / (self.hist.sum(axis=1) + self.hist.sum(axis=0) - np.diag(self.hist))
        miou = np.nanmean(iou) 
        
        # -----------------其他指标------------------------------
        # mean acc
        acc = np.diag(self.hist).sum() / self.hist.sum()
        acc_cls = np.nanmean(np.diag(self.hist) / self.hist.sum(axis=1))

        freq = self.hist.sum(axis=1) / self.hist.sum()
        fwavacc = (freq[freq > 0] * iou[freq > 0]).sum()

        return acc, acc_cls, iou, miou, fwavacc

 项目中的代码:

class Evaluator(object):
    def __init__(self, num_class):
        self.num_class = num_class
        self.confusion_matrix = np.zeros((self.num_class,)*2)#21*21的矩阵,行代表ground truth类别,列代表preds的类别,值代表

    '''
    正确的像素占总像素的比例
    '''
    def Pixel_Accuracy(self):
        Acc = np.diag(self.confusion_matrix).sum() / self.confusion_matrix.sum()
        return Acc

    '''
    分别计算每个类分类正确的概率
    '''
    def Pixel_Accuracy_Class(self):
        Acc = np.diag(self.confusion_matrix) / self.confusion_matrix.sum(axis=1)
        Acc = np.nanmean(Acc)
        return Acc

    '''

    Mean Intersection over Union(MIoU，均交并比)：为语义分割的标准度量。其计算两个集合的交集和并集之比.
    在语义分割的问题中，这两个集合为真实值（ground truth）和预测值（predicted segmentation）。
    这个比例可以变形为正真数（intersection）比上真正、假负、假正（并集）之和。在每个类上计算IoU，之后平均。
    
    对于21个类别,分别求IOU:
        例如,对于类别1的IOU定义如下:
            (1)统计在ground truth中属于类别1的像素数
            (2)统计在预测结果中每个类别1的像素数
                (1) + (2)就是二者的并集像素数(类比于两块区域的面积加和, 注:二者交集部分的面积加重复了)
                再减去二者的交集(既在ground truth集合中又在预测结果集合中的像素),得到的就是二者的并集(所有跟类别1有关系的像素:包括TP,FP,FN)
        扩展提示:
            TP(真正): 预测正确, 预测结果是正类, 真实是正类  
            FP(假正): 预测错误, 预测结果是正类, 真实是负类
            FN(假负): 预测错误, 预测结果是负类, 真实是正类
            
            TN(真负): 预测正确, 预测结果是负类, 真实是负类   #跟类别1无关,所以不包含在并集中
            (本例中, 正类:是类别1, 负类:不是类别1)
                
    mIoU:
        对于每个类别计算出的IoU求和取平均
    
    '''
    def Mean_Intersection_over_Union(self):
        MIoU = np.diag(self.confusion_matrix) / (
                    np.sum(self.confusion_matrix, axis=1) + np.sum(self.confusion_matrix, axis=0) -
                    np.diag(self.confusion_matrix))
        MIoU = np.nanmean(MIoU) #跳过0值求mean,shape:[21]
        return MIoU

    def Class_IOU(self):
        MIoU = np.diag(self.confusion_matrix) / (
                    np.sum(self.confusion_matrix, axis=1) + np.sum(self.confusion_matrix, axis=0) -
                    np.diag(self.confusion_matrix))
        return MIoU

    def Frequency_Weighted_Intersection_over_Union(self):
        freq = np.sum(self.confusion_matrix, axis=1) / np.sum(self.confusion_matrix)
        iu = np.diag(self.confusion_matrix) / (
                    np.sum(self.confusion_matrix, axis=1) + np.sum(self.confusion_matrix, axis=0) -
                    np.diag(self.confusion_matrix))

        FWIoU = (freq[freq > 0] * iu[freq > 0]).sum()
        return FWIoU


    '''
    参数的传入:
        evaluator = Evaluate(4)           #只需传入类别数4
        evaluator.add_batch(target, preb) #target:[batch_size, 512, 512]    ,    preb:[batch_size, 512, 512]
        在add_batch中统计这个epoch中所有图片的预测结果和ground truth的对应情况, 累计成confusion矩阵(便于之后求mean)
    
    
    参数列表对应:
        gt_image: target  图片的真实标签            [batch_size, 512, 512]
        per_image: preb   网络生成的图片的预测标签   [batch_size, 512, 512]
    
    parameters:
        mask: ground truth中所有正确(值在[0, classe_num])的像素label的mask---为了保证ground truth中的标签值都在合理的范围[0, 20]
        label: 为了计算混淆矩阵, 混淆矩阵中一共有num_class*num_class个数, 所以label中的数值也是在0与num_class**2之间. [batch_size, 512, 512]
        cout(reshape): 记录了每个类别对应的像素个数,行代表真实类别,列代表预测的类别,count矩阵中(x, y)位置的元素代表该张图片中真实类别为x,被预测为y的像素个数
        np.bincount: https://blog.csdn.net/xlinsist/article/details/51346523
        confusion_matrix: 对角线上的值的和代表分类正确的像素点个数(preb与target一致),对角线之外的其他值的和代表所有分类错误的像素的个数
    '''
    # 计算混淆矩阵
    def _generate_matrix(self, gt_image, pre_image):
        mask = (gt_image >= 0) & (gt_image < self.num_class)#ground truth中所有正确(值在[0, classe_num])的像素label的mask
        
        label = self.num_class * gt_image[mask].astype('int') + pre_image[mask] 
        # np.bincount计算了从0到n**2-1这n**2个数中每个数出现的次数，返回值形状(n, n)
        count = np.bincount(label, minlength=self.num_class**2)
        confusion_matrix = count.reshape(self.num_class, self.num_class)#21 * 21(for pascal)
        return confusion_matrix



# --------------------------------------------------------------------------------

    def add_batch(self, gt_image, pre_image):
        assert gt_image.shape == pre_image.shape
        tmp = self._generate_matrix(gt_image, pre_image)
        #矩阵相加是各个元素对应相加,即21*21的矩阵进行pixel-wise加和
        self.confusion_matrix += self._generate_matrix(gt_image, pre_image)


    def reset(self):
        self.confusion_matrix = np.zeros((self.num_class,) * 2)

其中, 利用计算出来的混淆矩阵计算MIoU的方法如下: 

    '''
        confusion_matrix是一个[num_classes,num_classes]的矩阵,
        confusion_matrix矩阵中(x, y)位置的元素代表该张图片中真实类别为x,被预测为y的像素个数
        第一个MIoU: [bach_size, 类别数]:对角线/(混淆矩阵各行加和+各列加和-对角线)
        第二个MIoU: [1, 类别数]
    '''
    def Mean_Intersection_over_Union(self):
        MIoU = np.diag(self.confusion_matrix) / (
                    np.sum(self.confusion_matrix, axis=1) +         
                    np.sum(self.confusion_matrix, axis=0) -
                    np.diag(self.confusion_matrix))
        MIoU = np.nanmean(MIoU) #跳过0值求mean,shape:[1, 21]
        return MIoU

后面是用fake数据帮助理解,可忽略:

其中a:预测值, b: ground truth

>>> b
array([[0, 0, 0, 2],
       [0, 0, 2, 1],
       [1, 1, 1, 0],
       [1, 0, 1, 2]])
>>> a
array([[0, 0, 0, 2],
       [0, 0, 2, 1],
       [1, 1, 1, 2],
       [1, 0, 1, 2]])
>>> label = 3 * b[mask] + a[mask]
>>> count = numpy.bincount(label)
>>> count
array([6, 0, 1, 0, 6, 0, 0, 0, 3])
>>> count = count.reshape(3, 3)
>>> numpy.sum(count, axis=1)
array([7, 6, 3])
>>> numpy.sum(count, axis=0)
array([6, 6, 4])
>>> numpy.sum(count, axis=1) + numpy.sum(count, axis=0)
array([13, 12,  7])
>>> numpy.sum(count, axis=1) + numpy.sum(count, axis=0) - numpy.diag(count)
array([7, 6, 4])

参考链接: https://blog.csdn.net/baidu_27643275/article/details/90445422