机器人运动学基础——旋转矩阵
旋转矩阵是机器人运动学的基础,但有时候经常会被各种旋转求解问题搞晕,比如旋转向量、旋转坐标系、同一空间点在不同坐标系下的坐标求解等等。正好当前需要对机械臂进行行为规划,所以又重新学习并理解了一下旋转矩阵,特此记录一下此次重温的结果。
文章目录
- 1. 本质理解
- 2. 基础概念
- 2.1 位置
- 2.2 姿态
- 3. 特例分析
- 3.1 向量的表示
- 3.2 向量的旋转
- 4. 感性总结
- 5. 参考文献
1. 本质理解
从本质上来理解,不管是坐标系中的向量旋转,还是同一空间点在不同坐标系的坐标求解等等,其最本质的原因都是坐标系之间的变换。所谓万变不离其宗,只要抓住了其本质属性,就不会再随便地被各种换着说法的求解问题搞晕。
因此在以下的介绍中会在不同的问题中寻找其共同点,总结出本质所在。
2. 基础概念
涉及到机器人运动学,就绕不开刚体的位姿这一概念,即刚体的位置和姿态。教材中的说明示意图如下图所示:

2.1 位置
刚体可以由其在空间中相对于参考坐标系的位置和方向进行完整的描述。在上图中假设 O − x y z O-xyz O−xyz 为标准正交参考坐标系,其中由蓝色箭头代表的 x , y , z \boldsymbol{ x,y,z} x,y,z为坐标轴的单位向量。
则刚体上的点 O ′ O' O′相对于坐标系 O − x y z O-xyz O−xyz的位置可以表示为: o ′ = o x ′ x + o y ′ y + o z ′ z \boldsymbol o'=o'_x\boldsymbol x+o'_y\boldsymbol y+o'_z\boldsymbol z o′=ox′x+oy′y+oz′z 其中 o x ′ , o y ′ , o z ′ o'_x, o'_y, o'_z ox′,oy′,oz′表示向量 o ′ \boldsymbol o' o′在参考坐标系的坐标轴上的分量。而 o ′ \boldsymbol o' o′的位置写为(3X1)的向量为: o ′ = [ o x ′ o y ′ o z ′ ] \boldsymbol o' = \begin{bmatrix} o'_x \\ o'_y \\ o'_z \end{bmatrix} o′=⎣⎡ox′oy′oz′⎦⎤而这个向量的完整描述可以表述为基与坐标的乘积: o ′ = [ x y z ] [ o x ′ o y ′ o z ′ ] \boldsymbol o' = \begin{bmatrix} \boldsymbol{x\, y\, z} \end{bmatrix} \begin{bmatrix} o'_x \\ o'_y \\ o'_z \end{bmatrix} o′=[xyz]⎣⎡ox′oy′oz′⎦⎤
2.2 姿态
除了位置之外,还需要对刚体的指向,即姿态进行描述。而这也是旋转矩阵最本质的来源,即来源于 坐标系的旋转,这一部分理解不好或是理解不透彻,会导致此后面对各种形式的旋转时出现混乱,所以公式将进行详细的表述。
描述姿态的方式就是为刚体建立一个固连于刚体的标准正交坐标系,并由 其相对于参考坐标系的 单位向量 在参考坐标系中的描述 来表示。如上图所示,刚体的局部固连参考系为 O − x ′ y ′ z ′ O-x'y'z' O−x′y′z′ ,其局部固连参考系坐标系的单位向量为 x ′ , y ′ , z ′ \boldsymbol{ x',y',z'} x′,y′,z′,而这局部坐标系的单位向量在参考坐标系 O − x y z O-xyz O−xyz 中的表示为: x ′ = a 1 x + a 2 y + a 3 z y ′ = b 1 x + b 2 y + b 3 z z ′ = c 1 x + c 2 y + c 3 z \boldsymbol x' = a_1\boldsymbol x + a_2\boldsymbol y + a_3\boldsymbol z \\ \boldsymbol y' = b_1\boldsymbol x + b_2\boldsymbol y + b_3\boldsymbol z \\ \boldsymbol z' = c_1\boldsymbol x + c_2\boldsymbol y + c_3\boldsymbol z x′=a1x+a2y+a3zy′=b1x+b2y+b3zz′=c1x+c2y+c3z其中 a 1 , a 2 , a 3 a_1, a_2, a_3 a1,a2,a3分别表示局部参考坐标系的 x ′ x' x′轴的基向量 x ′ \boldsymbol x' x′在参考坐标系 O − x y z O-xyz O−xyz 三个轴上的分量。其它的两轴同理。对于上式,可以进行进一步的整理,即上式等价于: [ x ′ y ′ z ′ ] = [ x y z ] [ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ] \boldsymbol{[x'\; y'\; z']} = \begin{bmatrix} \boldsymbol{x\; y\; z} \end{bmatrix} \begin{bmatrix} a_1\; b_1\; c_1 \\ a_2\; b_2\; c_2 \\ a_3\; b_3\; c_3 \end{bmatrix} [x′y′z′]=[xyz]⎣⎡a1b1c1a2b2c2a3b3c3⎦⎤最后一个矩阵就是两个坐标系基之间的关系,即两个坐标系之间的转换关系,将这个矩阵定义为旋转矩阵 R \boldsymbol R R。 R = [ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ] \boldsymbol R = \begin{bmatrix} a_1\; b_1\; c_1 \\ a_2\; b_2\; c_2 \\ a_3\; b_3\; c_3 \end{bmatrix} R=⎣⎡a1b1c1a2b2c2a3b3c3⎦⎤
通过计算过程也可以得出,当前这一旋转矩阵,是 O − x ′ y ′ z ′ O-x'y'z' O−x′y′z′ 坐标系相对于 O − x y z O-xyz O−xyz 的,同时需要注意的也有:旋转矩阵的每一列表示的是对应的刚体坐标系的基在原参考坐标系下的表示,所以每一列之间是相互正交的,且模长为1,所以旋转矩阵是一个正交矩阵,并且符合以下性质: R T R = I R T = R − 1 \boldsymbol{R^TR=I} \\ \boldsymbol{R^T=R^{-1}} RTR=IRT=R−1第二个性质说明,旋转矩阵的转置与其逆矩阵相等。
3. 特例分析
3.1 向量的表示
向量的表示问题其实就是同一空间点在不同坐标系下的求解问题,为了理解其几何意义,暂时不考虑坐标系之间的位移,即假设所有相关坐标系的原点重合。考虑一个坐标系(称之为新坐标系)通过参考坐标系(称之为旧坐标系)相对于某一旋转轴旋转得到。如果相对旋转轴作逆时针方向旋转,则旋转方向为正,反之则为负。如下图所示:
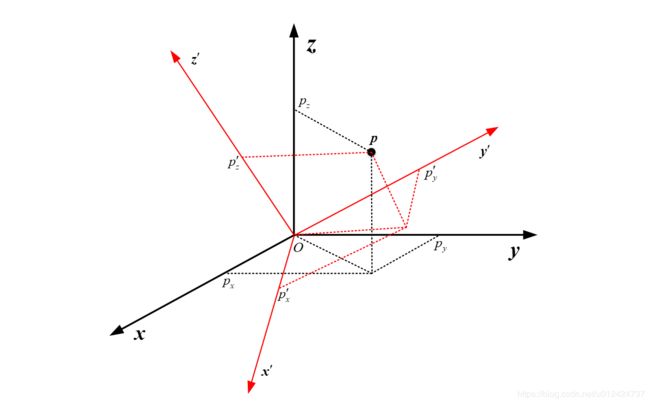
相对于旧坐标系 O − x y z O-xyz O−xyz,空间中的一点 P \boldsymbol P P 可以表示为 p = [ x y z ] [ p x p y p z ] \boldsymbol p = \begin{bmatrix} \boldsymbol{x\; y\; z} \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix} p=[xyz]⎣⎡pxpypz⎦⎤而相对于新坐标系 O ′ − x ′ y ′ z ′ O'-x'y'z' O′−x′y′z′,同一点可以表示为 p ′ = [ x ′ y ′ z ′ ] [ p x ′ p y ′ p z ′ ] \boldsymbol p' = \begin{bmatrix} \boldsymbol{x'\; y'\; z'} \end{bmatrix} \begin{bmatrix} p'_x \\ p'_y \\ p'_z \end{bmatrix} p′=[x′y′z′]⎣⎡px′py′pz′⎦⎤而以上两个方程式之间的唯一联系就是新旧坐标系之间的联系,即代表坐标系的基之间的联系。所以将上式与之前推导的坐标系之间的关系联立可以得到: p ′ = [ x ′ y ′ z ′ ] [ p x ′ p y ′ p z ′ ] = [ x y z ] [ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ] [ p x ′ p y ′ p z ′ ] \boldsymbol p' = \begin{bmatrix} \boldsymbol{x'\; y'\; z'} \end{bmatrix} \begin{bmatrix} p'_x \\ p'_y \\ p'_z \end{bmatrix} = \begin{bmatrix} \boldsymbol{x\; y\; z} \end{bmatrix} \begin{bmatrix} a_1\; b_1\; c_1 \\ a_2\; b_2\; c_2 \\ a_3\; b_3\; c_3 \end{bmatrix} \begin{bmatrix} p'_x \\ p'_y \\ p'_z \end{bmatrix} p′=[x′y′z′]⎣⎡px′py′pz′⎦⎤=[xyz]⎣⎡a1b1c1a2b2c2a3b3c3⎦⎤⎣⎡px′py′pz′⎦⎤因为 p , p ′ \boldsymbol{p, p'} p,p′在空间中是同一个点,当然 p , p ′ \boldsymbol{p, p'} p,p′的数值并不一样,但因为是空间中同一个点,所以如果将它们的坐标同时转换到同一个参考坐标系下,则数值必然是相等的,所以通过在同一基下的 p , p ′ \boldsymbol{p, p'} p,p′的表示式,可以得到纯坐标的关系为: [ p x p y p z ] = [ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ] [ p x ′ p y ′ p z ′ ] \begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix} = \begin{bmatrix} a_1\; b_1\; c_1 \\ a_2\; b_2\; c_2 \\ a_3\; b_3\; c_3 \end{bmatrix} \begin{bmatrix} p'_x \\ p'_y \\ p'_z \end{bmatrix} ⎣⎡pxpypz⎦⎤=⎣⎡a1b1c1a2b2c2a3b3c3⎦⎤⎣⎡px′py′pz′⎦⎤ 即新坐标系中的点左乘新坐标系相对于旧坐标系的旋转矩阵就等于当前点在旧坐标系中的位置。 从矩阵关系上可以很容易得出同一个点在不同坐标系下的坐标转换关系。但正如之前在第一部分所讲到的,这所有的旋转形式,不管是同一空间点在不同坐标系下的坐标关系还是向量的旋转求解,其本质都是坐标系之间的变换。那么如何从几何上理解同一点在不同坐标系下的不同表示这一问题呢?
如果想清楚其中的关键,其实很简单,甚至顺便把向量旋转的问题也解决了,那么其中的关键点是什么?用下图辅助说明:
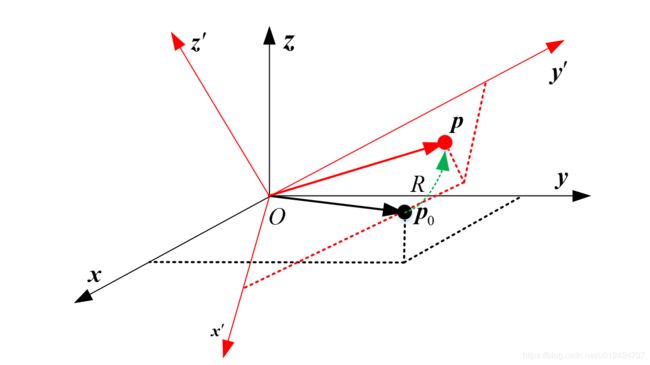
假设存在一个 p 0 \boldsymbol p_0 p0 点,位于旧坐标系中,其在旧坐标系中的坐标在数值上与 p \boldsymbol p p 点在新坐标系中的坐标完全相同。那么旧坐标系经过新坐标系相对于旧坐标系的旋转关系旋转之后, p 0 \boldsymbol p_0 p0 点与 p \boldsymbol p p 点必然是重合的。所以同一空间点在不同坐标系下的坐标求解问题,本质上是新旧坐标系之间的旋转变换问题,是旧坐标系带着与新坐标系中的点具有相同坐标数据的属于旧坐标系的点进行了新坐标系相对于旧坐标系旋转关系的旋转变换之后,所得到的点在旧坐标系中的坐标表示问题。 而这个问题,同时也是向量旋转问题。通过以上分析,可得出同一空间点在不同坐标系下的坐标求解问题的本质,是坐标系间的相对变换关系。想清楚了这一部分的几何解释,再来看向量的旋转问题。
3.2 向量的旋转
如下图所示,教科书中讲:旋转矩阵也可视为使某一向量绕空间中任一轴旋转给定角度的矩阵算子。从图中也可以看出,向量 p ′ \boldsymbol p' p′ 绕 z z z 轴旋转 α \alpha α 弧度之后,生成新的向量 p \boldsymbol p p。计算算式为 p = R z ( α ) p ′ \boldsymbol p = R_z(\alpha)\boldsymbol p' p=Rz(α)p′。

那从几何来说是为什么呢?其实这个例子比一个更直观,因为从几何上理解更容易一点,就是旧坐标系带着隶属于旧坐标系的向量 p ′ \boldsymbol p' p′绕着旧坐标系的 z z z 旋转了 α \alpha α 弧度之后,将向量 p ′ \boldsymbol p' p′绕到了现在向量 p \boldsymbol p p 的位置,所以向量 p \boldsymbol p p 的新坐标中的坐标数值就是向量 p ′ \boldsymbol p' p′在旧坐标系中的坐标数值。现在求解的就是这个随着旧坐标系到达新位置的向量 p ′ \boldsymbol p' p′在之前的旧坐标中的位置。
所以在计算上,当然是 新坐标系中的点左乘新坐标系相对于旧坐标系的旋转矩阵就等于当前点在旧坐标系中的位置。
4. 感性总结
经过这一次对旋转矩阵的重新学习与理解,试着将旋转相关的问题都解释为坐标系间的变换,将各种具有不同表象的问题统统归因于坐标系间的相对变换,返本归源。理解上又透彻了一分。
5. 参考文献
[1] Bruno Siciliano, Lorenzo Sciavicco, Luigi Villani, Giuseppe Oriolo. Robotics:Modeling,Planning and Control[M]. Springer-Verlag London, 2009.