Eigen使用的坑
先记录一个很详细的博客,还没完全看懂,后面再看
欧拉角、四元数、旋转矩阵推导及相互关系
1、切记Eigen的类型不会自动转换
YOU_MIXED_DIFFERENT_NUMERIC_TYPES__YOU_NEED_TO_USE_THE_CAST_METHOD_OF_MATRIXBASE_TO_CAST_NUMERIC_TYPES_EXPLICITLY2、Eigen中的向量其实就是单行矩阵,就是这么定义的
typedef float T;
typedef Eigen::Matrix Vector3t;
typedef Eigen::Matrix Matrix4t;
typedef Eigen::Matrix VectorXt;//列向量,列数是1 3、欧拉角转四元数&&四元数转欧拉角
float roll = 1.5707, pitch = 0, yaw = 0.707;
Quaternionf q;
q = AngleAxisf(roll, Vector3f::UnitX())
* AngleAxisf(pitch, Vector3f::UnitY())
* AngleAxisf(yaw, Vector3f::UnitZ());
std::cout << "Quaternion" << std::endl << q.coeffs() << std::endl;
std::cout << q.matrix().eulerAngles(0,1,2) << endl;4、角速度不能用欧拉角旋转表示,这是在跟自己自找麻烦!!!!为什么不先用简单的来让自己少犯错误呢??
这里在由增量角度计算四元数时,应该不是绕固定轴转的,就是正常的绕某个顺序转的,但是我从惯导拿到的角速度确是围绕固定轴算的,是真真正正的单轴的,所以会出错!!!
自己之所以一开始算的数值相差比较小,是因为在水平面上,roll和pitch都比较小,导致这两个值对yaw的影响比较小!!!
详见下面程序输出,如果把roll,pitch,以及droll,dpitch都改小一点,差别就不大了
#include
#include
using namespace Eigen;
using namespace std;
int main(int argc, char **argv)
{
//原始角度
float roll=1, pitch=1, yaw=1.4;
Quaternionf q;
q = AngleAxisf(roll, Vector3f::UnitX())
* AngleAxisf(pitch, Vector3f::UnitY())
* AngleAxisf(yaw, Vector3f::UnitZ());
std::cout <<"原始角度:"< 5、又一个坑!!!
这里给了自己一个很好的教训,先拿一些特殊例子看看,不要一开始就0 0 0
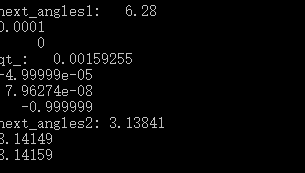
Vector3f next_angles = angles + raw_gyro * dt;
next_angles << 6.28, 0.0001, 0;
cout << "next_angles1: " << next_angles << endl;
Quaternionf qt_ = AngleAxisf(next_angles[0], Vector3f::UnitX())
* AngleAxisf(next_angles[1], Vector3f::UnitY())
* AngleAxisf(next_angles[2], Vector3f::UnitZ());
qt_.normalize();
cout << "qt_: " << qt_.coeffs() << endl;
cout << "next_angles2: " <输出结果:
本来输入的相当于0,0,0,但是结果却相差了PI。这是由于四元数表示的三维的旋转,而不是表示一个角度。
图例分析:
就跟名词和动词的区别一样。由惯导读出的欧拉角,其本来是表示一个角度,是一个名词。但是当表示旋转时,欧拉角的特定顺序也赋予了它能够表示旋转的功能,换句话说,roll,pitch,yaw不仅能表示一个姿态,也能表示一个旋转。当它表示一个姿态的时候,旋转的固定轴是没有发生变化的;但是当它表示一个旋转动作的时候,在它转换为四元数或者旋转矩阵时,其旋转轴发生了变换!!!
我所迷惑的是,我记得有两种转换方式,一种是绕固定轴,一种是绕自己的轴,那么到底是按哪个轴的???谁能解答一下