深度模型中的优化

深度模型中的优化

1、学习与纯优化有什么不同

2、神经网络优化中的挑战

3、基本算法

4、自适应学习率算法

5 、优化策略与元算法

学习与纯优化差别

1、机器学习算法的目标是降低泛化误差，即 J∗(θ)=E(x,y)→pdataL(f(x;η),y) J ∗ ( θ ) = E ( x , y ) → p d a t a L ( f ( x ; η ) , y ) ，但事实上pdata我们不知道，我们只知道训练集，因此机器学习问题转化为最优化训练集上的期望损失，即利用训练集上的分布来代替 p^ p ^ (x,y)来替代真实的 p(x,y) p ( x , y ) ,即最小化经验风险 J(θ)=E(x,y)→p^dataL(f(x;η),y)=1m∑mi=1L(f(xi;η),yi) J ( θ ) = E ( x , y ) → p ^ d a t a L ( f ( x ; η ) , y ) = 1 m ∑ i = 1 m L ( f ( x i ; η ) , y i )

2、现代优化方法是基于梯度下降的，有些经验损失函数，比如0-1损失，没有有效的导数，因此，我们通常会优化代理损失函数(surrogate loss function)，比如交叉熵损失函数。

3、机器学习算法中的优化算法在计算参数的每一次更新时通常仅使用代价函数中一部分项来估计代价函数的期望值，在整个数据集的每个样本上的损失来评估模型，代价非常大，实践中，可以从数据集中随机采样少量的样本，然后计算这些样本的平均值。

​ (1)n个样本均值的标准差为 σ/n−−√ σ / n ,基于100个样本和10000个样本，后者需要的计算量是前者的100倍，但是却只降低了10倍的标准差。因此，小批量算法会收敛的更快。

​ (2)一个原因是训练集中大量样本都对梯度做出相似的贡献

小批量的大小由以下因素决定：

(1)、更大的批量会更精确梯度计算，但是回报是现行的

(2)、极小批量难以充分利用多核架构，更小批量处理不会减少计算时间

(3)、所有样本参与训练，对内存要求过高，硬件不支持

(4)、通常采用2的幂数来作为批量大小可以获得更少的运行时间，一般选32-256

(5)、小批量算法在学习过程中加入了噪声，因此，会有一定的正则化效果。

小批量要求随机抽取，因此常常需要打乱样本顺序

神经网络优化中的挑战

传统机器学习会小心设计目标函数和约束，以确保优化问题是凸的，但训练神经网络时，一定会遇到非凸情况。

1、局部极小点

2、高原、鞍点和平坦区域：由于神经网络参数维度非常高，局部极小点出现的机会非常小，鞍点则更常见，鞍点附近的梯度非常小，但实验中梯度下降似乎可以逃离鞍点。除了鞍点和极小点，也可能存在高原、平坦区域，此时梯度和Hessian矩阵都是零，这是所有优化问题的主要问题。

3、梯度爆炸：训练非常深的神经网络或循环神经网络时，会出现像悬崖一样的斜率较大的区域，这是由于几个较大的权重相乘 导致的，遇到斜率较大的悬崖结构是，梯度更新会很大程度改变参数值，我们可以采用启发式的梯度截断 来避免，传统梯度下降至说明无限小区域内的最佳方向，但没有说明最佳步长，当梯度下降提议更新很大一步时，梯度截断会干涉以减小步长，循环神经网络中非常常见。

4、长期依赖 ：当计算图变得极深时，由于变深的结构使得模型丧失了学习到先前信息的能力，让优化变得及其困难，因为循环神经网络要在很长时间序列的各个时刻重复应用相同操作来构建非常深的计算图，并且模型参数共享，问题会更严重。例如，假设某个计算图中包含一条反复与矩阵W相乘的路径，经过t步后，相当于乘以 Wt W t ,假设W可分解为 W=Vdiag(λ)V−1 W = V d i a g ( λ ) V − 1 ,则 Wt=Vdiag(λt)V−1 W t = V d i a g ( λ t ) V − 1 ,当t比较大时， λi λ i 大于1，会发生梯度爆炸(exploding gradient) ， λi λ i 小于1，则会出现梯度消失(vanishing gradient) 。梯度消失会使得我们难以知道朝那个方向移动能改进代价函数，而梯度爆炸会使得学习不稳定。 xTWt x T W t 随着t的增加，最终会丢失点x中的有效信息（稳定状态只与W有关）

前馈神经网络中即使非常深的网络，也能很大程度上有效避免梯度消失于梯度爆炸的问题。

基本算法

随机梯度下降 (SGD)：基本训练方法，超参数：学习率

动量 (momentum)：动量算法主要有两个作用：

1、解决随机梯度下降算法梯度的高方差问题，使摆动不至于太剧烈：增加动量项，可以近似认为增加了梯度的采样的样本数(最近时间的梯度会有比较大的权重)，根据 σ/n−−√ σ / n 可知,方差减小

2、加大了步长，提高了收敛速度：每一次梯度都包含正确的梯度方向和方差引起的摆动，增加动量，相当于将之前多个梯度叠加，增加了共同方向(期望梯度方向)，因此，相等与增大了步长。

具体操作如下:

on iteration t:

​ compute dW,db on the current mini-batch

​ vdw=βvdw+(1−β)dWt v d w = β v d w + ( 1 − β ) d W t

​ vdb=βvdb+(1−β)dbt v d b = β v d b + ( 1 − β ) d b t

​ Wt+1=Wt−αvdW W t + 1 = W t − α v d W

​ bt+1=bt−αvdb b t + 1 = b t − α v d b

python 实现

1、初始化V
def initialize_velocity(parameters):
“””
Initializes the velocity as a python dictionary with:
- keys: “dW1”, “db1”, …, “dWL”, “dbL”
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters – python dictionary containing your parameters.
parameters[‘W’ + str(l)] = Wl
parameters[‘b’ + str(l)] = bl

Returns:
v -- python dictionary containing the current velocity.
                v['dW' + str(l)] = velocity of dWl
                v['db' + str(l)] = velocity of dbl
"""

L = len(parameters) // 2 # number of layers in the neural networks
v = {}

# Initialize velocity
for l in range(L):
    ### START CODE HERE ### (approx. 2 lines)
    v["dW" + str(l+1)] = np.zeros_like(parameters["W" + str(l+1)])
    v["db" + str(l+1)] = np.zeros_like(parameters["b" + str(l+1)])
    ### END CODE HERE ###

return v

2、更新权值

def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
Update parameters using Momentum

Arguments:
parameters -- python dictionary containing your parameters:
                parameters['W' + str(l)] = Wl
                parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
                grads['dW' + str(l)] = dWl
                grads['db' + str(l)] = dbl
v -- python dictionary containing the current velocity:
                v['dW' + str(l)] = ...
                v['db' + str(l)] = ...
beta -- the momentum hyperparameter, scalar
learning_rate -- the learning rate, scalar

Returns:
parameters -- python dictionary containing your updated parameters 
v -- python dictionary containing your updated velocities
"""

L = len(parameters) // 2 # number of layers in the neural networks

# Momentum update for each parameter
for l in range(L):

    ### START CODE HERE ### (approx. 4 lines)
    # compute velocities
    v["dW" + str(l+1)] = beta *v["dW" + str(l+1)] +(1-beta)*grads["dW" + str(l+1)]
    v["db" + str(l+1)] = beta *v["db" + str(l+1)] +(1-beta)*grads["db" + str(l+1)]
    # update parameters
    parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v["dW" + str(l+1)]
    parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v["db" + str(l+1)]
    ### END CODE HERE ###

return parameters, v

超参数 ： α和β α 和 β ， β β 一般取0.9，0.99

自适应学习率算法

学习率是神经网络中难以设置的超参数之一，对模型的性能有显著的影响，因此需要自适应的学习率算法，更好的学习率参数一方面可以加速收敛，一方面可以减小训练误差，本文主要介绍：AdaGrad 、RMSProp、Adam

AdaGrad : Wt+1=Wt−ηt+1√1t+1∑ti=0(gi)2√dWt=Wt−η∑ti=0(gi)2√dWt W t + 1 = W t − η t + 1 1 t + 1 ∑ i = 0 t ( g i ) 2 d W t = W t − η ∑ i = 0 t ( g i ) 2 d W t （求和和开根号都是元素级别的）

AdaGrad 自适应的为每个参数提供自适应的权重，如果某个梯度历史积累具有较大的梯度（调整已经比较大），那么给一个小的学习率（除以一个更大的值），相反，如果某个梯度历史积累相对较小（调整不是很大），则给比较大的学习率，净效果是在较为平缓的方向取得比较大的进步,有助于逃离高原平台。但是从训练开始积累平方和可能会导致有效学习率过早过过量的减小。

RMSProp

RMSProp 修改了AdaGrad梯度累加的方式，采用指数加权移动平均（丢弃时间过久的历史），多了一个超参数 β β ,用以控制移动平均的长度范围。

on iteration t:

​ compute dW,db on the current mini-batch

​ Sdw=βSdw+(1−β)(dWt)2 S d w = β S d w + ( 1 − β ) ( d W t ) 2

​ Sdb=βSdb+(1−β)(dbt)2 S d b = β S d b + ( 1 − β ) ( d b t ) 2

​ Wt+1=Wt−αdWtSdw+ϵ√ W t + 1 = W t − α d W t S d w + ϵ

​ bt+1=Wt−αdbtSdb+ϵ√ b t + 1 = W t − α d b t S d b + ϵ

Adam

Adam可以认为是将动量算法和RMSProp结合起来使用,将动量替换RMSProp中的梯度，同时Adam对动量和指数加权均分都做了偏差修正，因此更加鲁棒，超参数 β1 β 1 (momentum) β2 β 2 (RMSProp)。

on iteration t:

​ compute dW,db on the current mini-batch

​ vdw=β1vdw+(1−β1)dWt v d w = β 1 v d w + ( 1 − β 1 ) d W t

​ vdb=β1vdb+(1−β1)dbt v d b = β 1 v d b + ( 1 − β 1 ) d b t

​ vcorrectdw=vdw/(1−βt1) v d w c o r r e c t = v d w / ( 1 − β 1 t )

​ vcorrectdb=vdb/(1−βt1) v d b c o r r e c t = v d b / ( 1 − β 1 t )

​ Sdw=β2Sdw+(1−β2)(dWt)2 S d w = β 2 S d w + ( 1 − β 2 ) ( d W t ) 2

​ Sdb=β2Sdb+(1−β2)(dbt)2 S d b = β 2 S d b + ( 1 − β 2 ) ( d b t ) 2

​ Scorrectdw=Sdw/(1−βt2) S d w c o r r e c t = S d w / ( 1 − β 2 t )

​ Scorrectdb=Sdb/(1−βt2) S d b c o r r e c t = S d b / ( 1 − β 2 t )

​ Wt+1=Wt−αvcorrectdwScdworrect+ϵ√ W t + 1 = W t − α v d w c o r r e c t S d w c o r r e c t + ϵ

​ bt+1=Wt−αvcorrectdbScorrectdb+ϵ√ b t + 1 = W t − α v d b c o r r e c t S d b c o r r e c t + ϵ

python 实现

def initialize_adam(parameters) :
"""
Initializes v and s as two python dictionaries with:
            - keys: "dW1", "db1", ..., "dWL", "dbL" 
            - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.

Arguments:
parameters -- python dictionary containing your parameters.
                parameters["W" + str(l)] = Wl
                parameters["b" + str(l)] = bl

Returns: 
v -- python dictionary that will contain the exponentially weighted average of the gradient.
                v["dW" + str(l)] = ...
                v["db" + str(l)] = ...
s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
                s["dW" + str(l)] = ...
                s["db" + str(l)] = ...

"""

L = len(parameters) // 2 # number of layers in the neural networks
v = {}
s = {}

# Initialize v, s. Input: "parameters". Outputs: "v, s".
for l in range(L):
### START CODE HERE ### (approx. 4 lines)
    v["dW" + str(l+1)] = np.zeros_like(parameters['W' + str(l+1)])
    v["db" + str(l+1)] = np.zeros_like(parameters['b' + str(l+1)])
    s["dW" + str(l+1)] = np.zeros_like(parameters['W' + str(l+1)])
    s["db" + str(l+1)] = np.zeros_like(parameters['b' + str(l+1)])
### END CODE HERE ###

return v, s

def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
“””
Update parameters using Adam

Arguments:
parameters -- python dictionary containing your parameters:
                parameters['W' + str(l)] = Wl
                parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
                grads['dW' + str(l)] = dWl
                grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates 
beta2 -- Exponential decay hyperparameter for the second moment estimates 
epsilon -- hyperparameter preventing division by zero in Adam updates

Returns:
parameters -- python dictionary containing your updated parameters 
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""

L = len(parameters) // 2                 # number of layers in the neural networks
v_corrected = {}                         # Initializing first moment estimate, python dictionary
s_corrected = {}                         # Initializing second moment estimate, python dictionary

# Perform Adam update on all parameters
for l in range(L):
    # Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
    ### START CODE HERE ### (approx. 2 lines)
    v["dW" + str(l+1)] = beta1 * v["dW" + str(l+1)] + (1-beta1) * grads['dW' + str(l+1)]
    v["db" + str(l+1)] = beta1 * v["db" + str(l+1)] + (1-beta1) * grads['db' + str(l+1)]
    ### END CODE HERE ###

    # Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
    ### START CODE HERE ### (approx. 2 lines)
    v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)] / (1- np.power(beta1,t))
    v_corrected["db" + str(l+1)] = v["db" + str(l+1)] / (1- np.power(beta1,t))
    ### END CODE HERE ###

    # Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
    ### START CODE HERE ### (approx. 2 lines)
    s["dW" + str(l+1)] = beta2 * s["dW" + str(l+1)] + (1- beta2) * np.square(grads['dW' + str(l+1)])
    s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1- beta2) * np.square(grads['db' + str(l+1)])
    ### END CODE HERE ###

    # Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
    ### START CODE HERE ### (approx. 2 lines)
    s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)] / (1-np.power(beta2,t))
    s_corrected["db" + str(l+1)] = s["db" + str(l+1)] / (1-np.power(beta2,t))
    ### END CODE HERE ###

    # Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
    ### START CODE HERE ### (approx. 2 lines)
    parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v_corrected["dW" + str(l+1)] /np.sqrt(s_corrected["dW" + str(l+1)] +epsilon)
    parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v_corrected["db" + str(l+1)] /np.sqrt(s_corrected["db" + str(l+1)] +epsilon)
    ### END CODE HERE ###

return parameters, v, s

优化策略与元算法

Batch norm(批标准化)

Batch norm（批标准化）可以有效解决covariate shift 的问题，并有轻微的正则化的效果，可以让大型神经网络训练速度加快很多倍，同时收敛后的分类准确率也可以得到大幅提高。

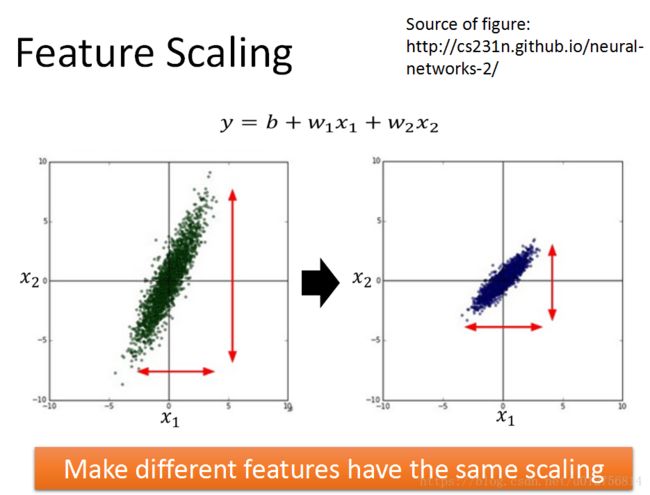
进行logistic regression 时，如果我们对输入信息进行标准化，将不同的特征比例到同一尺度下，会使得训练变得更加快速，在深层网络训练中，对输入层和每一个隐藏层都进行标准化处理。

μ=1m∑mi=1zli μ = 1 m ∑ i = 1 m z i l

σ2=1m∑mi=1(zli−μ)2 σ 2 = 1 m ∑ i = 1 m ( z i l − μ ) 2

z~lnorm，i=zli−μσ2+ϵ√ z ~ n o r m ， i l = z i l − μ σ 2 + ϵ

但是标准化一个单元的均值和标准差会降低包含该单元的神经网络的表达能力，为了保持网络的表现力，通常需要将标准化后的 z~lnorm，i z ~ n o r m ， i l 做如下操作，通过激活函数。 z~li=γz~lnorm，i+β z ~ i l = γ z ~ n o r m ， i l + β ,其中 γ和β γ 和 β 是需要学习的参数。 γ和β γ 和 β 使得新的隐藏单元可能有任何的均值和标准差，只所以这样操作，是因为原来的神经网络中，某一隐藏层的均值和方差是由前层所有参数共同决定，而采用batch_norm 则只由 γ和β γ 和 β 决定，使得每一隐藏层的训练相对稳定，受前层影响更小，学习更加独立。

关于batch_norm还有几个细节需要说明：

1、每层训练时都要做标准化处理，因此不需要在每层假设偏置项b,因此，每一层需要学习的参数包括W, β β , γ γ

2、batch_norm 通常要采用mini_batch 方法进行训练，因此，利用每一个batch进行训练时，计算的均值和方差，都是该mini_batch 的均值和方差，因此与全部数据的均值和偏差有差别，正式这些差别，使得，batch_norm 有轻微的规则化的作用。

3、测试时，需要对每一个样本进行逐一处理 单个数据的均值和方差没有意义，需要单独计算均值和方差，理论上可以在整个数据上进行统计均值和方差，实际操作中，在训练时使用指数加权平均算法得到(只需要记住上一次加权，内存要求非常小)，这个值就是该隐藏层z均值、方差的估计。

总结来说：batch_norm 主要有一下三方面作用：

1、进行标准化处理，使训练变得更加容易，加速收敛

2、一定程度上解决了covariate shift 的问题，将每一隐藏层先进行标准化，在乘上 γ γ 加上 β β ，使得每一层的均值和方差只受 β β 和 γ γ 影响，因此，batch_norm限制了浅层参数的更新对该隐藏层分布的影响,即使输入分布有一些改变，改变也不会很大，使得网络每层之间学习更加独立，从而加速整个网络的学习。

3、batch_norm 采用mini_batch 数据计算均值和方差，引入了一些噪音，有轻微的正则化的作用，由于正则化效果不是很强，因此，可以和dropout一起使用。

因此，可以说batch_norm可以帮助训练更深的网络，使学习算法收敛的更快。

坐标下降

某些情况下，将一个优化问题分解成几个部分，可以更快的解决原问题。例如我们可以对某一单一变量 xi x i 最小化f，然后相对于另一个变量 xj x j 最小化f等等，反复循环所有变量，保证达到最小值，这种方法称为坐标下降（例如Kmeans算法）。更一般地，采用块坐标下降，将变量分解为多个子集，分别在某一个子集上进行最小化。

监督预训练

有时如果模型太复杂难以优化或是任务非常困难，直接训练模型来解决特定任务的挑战可能太大，因此，尝试在一个简单的问题上进行训练，然后转移到最后的问题，可能更有效些。贪心算法 将问题分解成许多部分，然后独立地在每个部分求解最优值，结合各个最佳的部分，并不能保证得到一个最佳的完整解，然后贪心算法相比求解最优联合解算法高效的多，并且贪心算法的解在不是最优的情况下，往往也是可以接受的。贪心算法可以紧接一个精调(fine-tine)阶段，联合优化算法搜索全问题的最优解，使用贪心解初始化联合优化算法，可以极大地加速算法，并提高寻找到的解的质量。应用：迁移学习

延拓法

许多优化挑战来自代价函数的全局结构，不能仅通过局部更新方向上更好的估计来解决。延拓法是一族通过挑选初始点使优化更容易的方法，以确保局部优化花费大部分时间在表现良好的空间。其思想是构造一系列具有相同参数的目标函数，为了最小化代价函数 J(θ) J ( θ ) ,我们构建新的代价函数{ J0,J1...Jn J 0 , J 1 . . . J n },这些代价函数的难度逐步提高，其中 J0 J 0 最容易优化， Jn J n 最难，这系列代价函数设计为浅一个解释下一个的良好的初始点，因此，我们先解决一个简单的问题，然后改进解以解决逐步变难得问题，直到我们求解真正问题的解。

传统延拓法基于平滑目标函数，传统延拓法主要用来解决局部极小值问题，具体地，这些代价函数族，会通过平滑（模糊）原来的代价函数，从而使某些非凸函数在模糊后会近似凸的（这种模糊保留了全局最小的足够信息）。但是有三种方式可能失败：1、可能需要非常多的逐步代价函数，整个过程的成本可能非常高。2、有些问题，不管如何模糊，都无法变成凸的，3、模糊函数的最小值可能会追踪到一个局部最小值，而非原始代价函数的全局最小值。

延拓法可以消除平坦区域。

课程学习基于规划学习过程的想法，首先从简单概念，然后逐步学习依赖于这些简单化概念的复杂概念，课程学习被证实与人类学习一致，基于课程学习的策略比基于样本均匀采用的策略更有效，能提高其他学习策略的效率。

课程学习的另一贡献在训练循环神经网络捕获长期依赖。

优化问题是机器学习最核心的问题，本文是在自习了吴恩达深度学习课程和lan Goodfellow<深度学习>有关优化章节后的总结，如果有问题，欢迎提出意见和建议，谢谢！