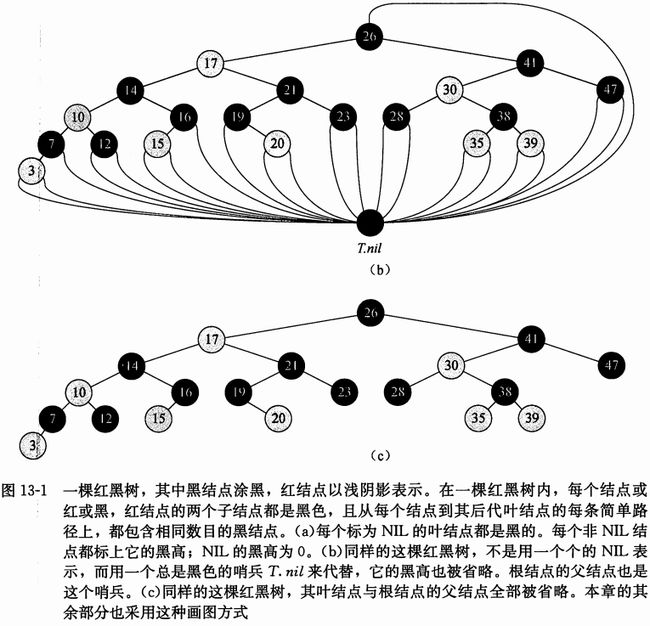
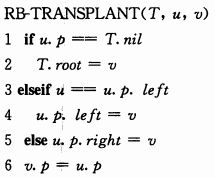红黑树理解 - 数据结构
红黑树
红黑树是很多平衡树的一种,保证最坏情况下基本动态几何操作时间复杂度为O(log(n))
1、红黑树性质
(1) 每个节点是红色的,或者是黑色的
(2) 根节点是黑色的
(3) 每个叶节点(nil)是黑色的
(4) 如果一个节点是黑色的,则它的连个子节点都是黑色的
(5) 对每个节点,从该节点到其后代叶节点的简单路径上,均包含相同数目的黑色节点
2、旋转
旋转是保持二叉搜索树局部性质的操作,包括左旋和右旋。当在节点x上做左旋时,假设它的右孩子为y而不是T.nil,X可为其右孩子不是T.nil的任何节点,同理,X做右旋也是一样的。

伪代码如下(左旋)

旋转代码(左旋-C)
static void left_rotate(rbTree *T, rbtreeNode * x)
{
rbtreeNode *y = x->right;
x->right = y->left;
if(y->left != T->nil)
y->left->p = x;
y->p = x->p;
if(x->p == T->nil)
T->root = y;
else if(x == x->p->left)
x->p->left = y;
else
x->p->right = y;
y->left = x;
x->p = y;
}3、插入
在O(log(n))时间内插入一个节点,RB-INSERT过程完成该操作,像一个普通的二叉搜索树一样,然后将要插入的节点Z着为红色。为了保持红黑树的性质,调用一个辅助函数RB-INSERT-FIXUP来对节点从新着色并旋转。待插入节点Z已保存了数据项。
RB-INSERT过程伪代码

RB-INSERT-FIXUP过程伪代码

注意:Case1属于if判断条件中,Case2和Case3输入else语句中的,Case2是else语句中的if判断语句的。具体可以看代码
RB-INSERT代码实现(C)
int rbtree_insert(rbTree *T, DataTypedef num)
{
rbtreeNode *y = T->nil;
rbtreeNode *x = T->root;
rbtreeNode *z = NULL;
if(!rbtree_in(T, num))
{
z = (rbtreeNode *)malloc(sizeof(rbtreeNode));
if(z == NULL)
err_sys("no space for z in rbtree");
z->data = num;
}
else
return ERR;
while(x != T->nil) //y is parent point of x
{
y = x;
if(z->data < x->data)
x = x->left;
else
x = x->right;
}
z->p = y;
if(y == T->nil)
T->root = z;
else if(z->data < y->data)
y->left = z;
else
y->right = z;
z->left = T->nil;
z->right = T->nil;
z->color = RED;
if( rbtree_fixup(T, z) )
return OK;
else
return ERR;
}RB-INSERT-FIXUP过程分析
第1-15行的while循环在每次迭代的开始始终保持以下3个条件是不变的
(1) 节点z是红节点
(2) 如果z.p是根节点,则z.p是黑节点
(3) 如果有任何红黑树性质贝破坏,则至多有一条被破坏,或是性质2,或是性质4(各个性质见红黑树性质总结)。如果性质2被破坏,则因为z是根节点且是红节点。性质4被破坏则是因为z和z.p都是红节点。
循环终止条件:
循环终止因为z.p是黑色的(如果z是根节点,则z.p是黑色哨兵节点),这样,在循环终止时并没有违反性质4,唯一可能不成立的就是性质2,不过第16行恢复了这个性质。
循环保持条件:
循环保持有6中条件,其中3种和另外3种是对称的,这取决于z的父节点z.p是z的祖父节点z.p.p的左孩子还是右孩子。情况1、2、3的区别就在于z的父节点的兄弟节点(z的叔节点)的颜色不同,加入y指向z的叔节点,如果y的颜色是红色的,则执行情况1,否则转向情况2和3。在所有的3种情况中,z的祖父节点z.p.p是黑色的,因为他的父节点z.p是红色的,故性质4只有在z和z.p之间被破坏了。
情况1:z的叔节点y是红色的
此时对应Case1,将z.p和y都着成黑色,解决z和z.p都是红色的问题,将z.p.p着成红色保持性质5,然后把z.p.p作为新节点z来继续进行while循环,指针z上移两层
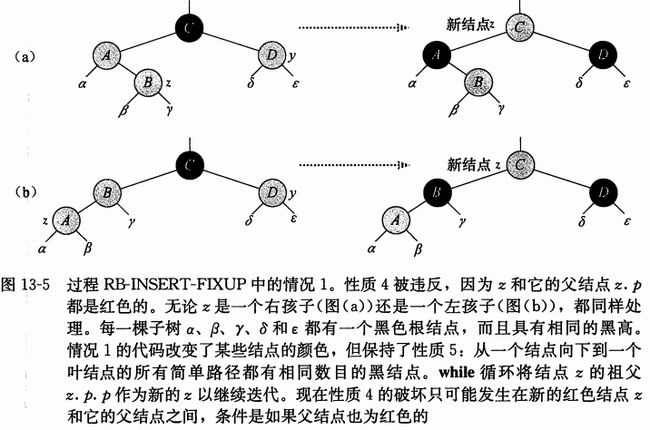
情况2:z的叔节点y是黑色的且z是一个右孩子
情况3:z的叔节点y是黑色的且z是一个左孩子
两种情况中,y都是黑色的,通过z是左孩子还是右孩子来区分,情况2中可以通过一个左旋来转化为情况3,此时z为左孩子。因为z和z.p都是红节点,对黑高(从某个节点出发,不含该节点,到达一个叶节点的任意一条简答路径上的黑色节点数为该节点的黑高)和性质5都无影响。在情况3中,改变某些节点颜色并做一次右旋,保持性质5,这样不在有两个红色节点相邻,处理完毕,此时z.p是黑色的,所以无需再执行while循环了。
RB-INSERT-FIXUP代码实现(C)
static int rbtree_fixup(rbTree *T, rbtreeNode *z)
{
rbtreeNode *y = NULL;
/*
* while循环在每次迭代的开头都保持3个部分的不变式
* 1 节点z是红色节点
* 2 如果z.p是根节点,则z.p是黑节点
* 3 如果有任何红黑性质被破坏,则至多只有一条被破坏,或是性质2(根为黑色节点),或是性质4(如果一个节点是红色的,
* 则它的两个子节点都是黑色的)
*/
while(z->p->color == RED)
{
if(z->p == z->p->p->left)//在所有的情况中,z的祖父节点z.p.p是黑色的,以为z.p是红色的
{
y = z->p->p->right;
// Case1: z uncle node y is red
if(y->color == RED)
{
z->p->color = BLACK;
y->color = BLACK;
z->p->p->color = RED;
z = z->p->p;
}
else
{
// Case2: z uncle node y is black, but z is right node
if(z == z->p->right)
{
z = z->p;
left_rotate(T, z);
}
// Case3: z uncle node y is black, but z is left node
z->p->color = BLACK;
z->p->p->color = RED;
right_rotate(T, z->p->p);
}
}
else
{
y = z->p->p->left;
if(y->color == RED)
{
z->p->color = BLACK;
y->color = BLACK;
z->p->p->color = RED;
z = z->p->p;
}
else
{
if(z == z->p->left)
{
z = z->p;
right_rotate(T, z);
}
z->p->color = BLACK;
z->p->p->color = RED;
left_rotate(T, z->p->p);
}
}
}
T->root->color = BLACK;
return OK;
}4、删除
删除操作与插入操作相比,略显复杂,与插入操作一样,也要花费O(log(n))时间。
从红黑树中删除节点,需设计一个供TREE-DELETE调用的子过程TRANSPLANT,并应用到红黑树中,TRANSPLANT过程用来调整两个节点的关系,其中的一个节点要替换掉另一个节点
TRANSPLANT过程
u节点表示将要被替换掉的节点,v节点是准备替换u节点的
RB-TRANSPLANT代码实现(C)
static void rbtree_transplant(rbTree *T, rbtreeNode *u, rbtreeNode *v)
{
if(u->p == T->nil)
{
T->root = v;
}
else if(u == u->p->left)
{
u->p->left = v;
}
else
{
u->p->right = v;
}
v->p = u->p;
}RB-DELETE过程
RB-DELETE中,z节点是要被删除的节点,其中记录了节点y的踪迹,y有可能导致红黑树性质破坏,当想删除节点z,且z的子节点少于2个时,z从书中删除,并让y称为z。当z有两个子节点时,y应该是z的后继,并且将y移到z的位置。在节点被删除或者移动时,必须记住y的颜色,并且记录节点x的踪迹,将x移到y的原来的位置,因为节点x可能引起红黑树性质破坏。删除节点z后,RB-DELETE-FIXUP过程通过改变颜色和执行旋转来恢复红黑树性质。

我们保存节点x的踪迹,使它移至节点y的原来位置。第4、7和11行的赋值语句令x或指向y的唯一子节点或指向y哨兵T.nil(y没有子节点的话)。
第5、8或14行调用RB-TRANSPLANT时,传递的第2个参数与x相同
如果y是黑色的,则有可能引入一个或多个破坏红黑色的情况,所以在第22行调用RB-TRANSPLANT来恢复红黑树性质。如果y是红色的,当y被删除或移动时,红黑树性质依然成立,因为(1) 树中黑高没有变化 (2) 不存在两个相邻的红节点,因为y在树中占据了z的位置,z的位置肯定不会违反红黑树性质的。另外,如果y是z的右孩子,则y的原右孩子x代替y,如果y是红色的,则x一定是黑色的,一次用x替代y不会使两个红节点相邻。 (3) 如果y是红色的,就不会是根节点,所以根节点仍然是黑色的。
y为黑节点情况分析
RB-DELETE代码实现(C)
void rbtree_delete(rbTree *T, DataTypedef data)
{
rbtreeNode *z = rbtree_find(T, data);
rbtreeNode *y;
rbtreeNode *x;
enum ColorTypedef y_oldcolor;
if(z == T->nil)
{
printf("the rbtree hasn't %d\n", data);
return;
}
y = z;
y_oldcolor = y->color;
if(z->left == T->nil)
{
x = z->right;
rbtree_transplant(T, z, z->right);
}
else if(z->right == T->nil)
{
x = z->left;
rbtree_transplant(T, z, z->left);
}
else
{
y = rbtree_findmin(T, z->right);
y_oldcolor = y->color;
x = y->right;
if(y->p == z)
{
x->p = y;
}
else
{
rbtree_transplant(T, y, y->right);
y->right = z->right;
y->right->p = y;
}
rbtree_transplant(T, z, y);
y->left = z->left;
y->left->p = y;
y->color = z->color;
}
if(y_oldcolor == BLACK)
rbtree_delete_fixup(T, x);
free(z);
//printf("free the node is ok\n\n");
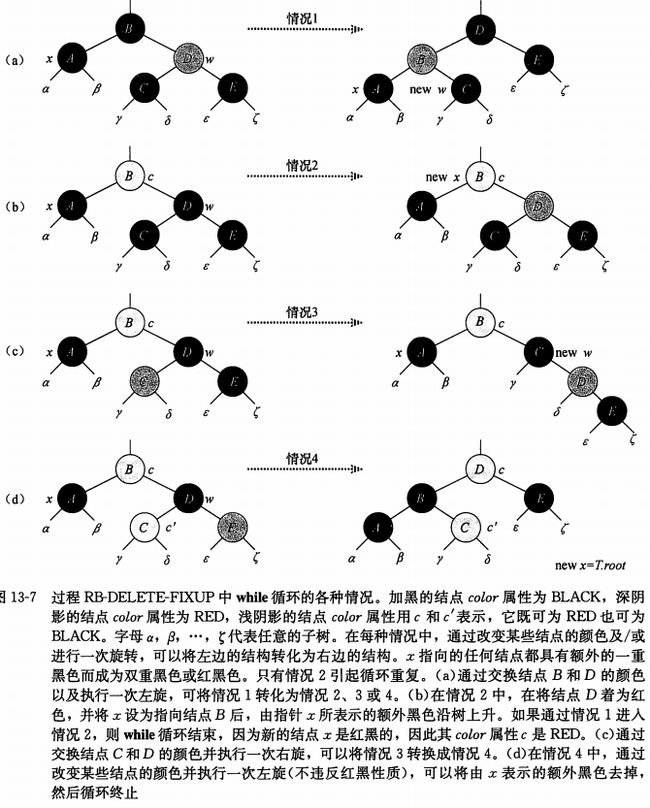
}RB-DELETE-FIXUP过程

ps:图片上的情况层次关系对应不是很齐,可以看码来的清楚
4中情况的转换关系
1 -> 2、3、4
2 -> 1、2、3、4、修复 (只有Case2是节点上移,所有有可能会使x=root)
3 -> 4
4 -> 修复
无论哪个Case,要么是为了到达平衡两个节点,路径上黑色数目相同的目的,要么是通过变形间接达到这个目的。
while循环的目标是将额外的黑色沿树上移,直到:
(1) x指向红黑节点,此时在第23行处将x着为(单个)黑色
(2) x指向根节点,此时可以简单地移除额外的黑色
(3) 执行适当的旋转和重新着色

代码中的4种情况图示
上图给出了代码中出现的四种情况,再具体研究每一个情况时,先看看如何证实每种情况中的变换保证性质5。关键思想是在每种情况下,从子树的跟(包括跟)到每棵子树之间的黑色节点个数(包括x的额外黑色)并不被变换改变,因此,如果性质5在变换之前成立,则在变换之后也成立。比如:在情况1中,在变换前后,根节点到子树a或b之间的黑色节点数是3(因为x增加了一层黑色),类似的,在变换前后根节点到其余的4个子树的叶节点中的任何一个的黑节点数是2。在图13-7(b)中,计数是还要包括所示子树的根节点的color属性的值,它是RED或是BLACK,如果定义count(RED)=0以及count(BLACK)=1,那么变换前后根节点至a的黑节点都为2+count(c)。在此情况下,变换之后新节点x具有color属性的c,但是这个节点的颜色是红黑(如果c=RED)或者双重黑色的(如果c=BLACK)。其他情况可以类似加以验证。
情况1:x的兄弟节点w是红色的
情况1(见RB-DELETE-FIXUP的第5-8行和图13-7(a))发生在节点x的兄弟节点w为红色时。因为w必须有黑色子节点,所有可以改变w的x.p的颜色,然后对x.p做一次左旋而不违反红黑树的任何性质。现在x的新兄弟节点是旋转之前w的某个子节点,其颜色为黑色。这样,就将情况1转变为了情况2、3或者4。
当节点w为黑色时,属于情况2、3或者4;这些情况有w的子节点颜色来区分了。
情况2:x的兄弟节点w是黑色的,而且w的两个子节点都是黑色的
在情况2(见RB-DELETE-FIXUP的第10-11行和图13-7(b)),w的两个子节点都是黑色的,因为w也是黑色的,所以从x和w上去掉一重黑色,使得x只有一重黑色而w为红色。为了补偿从x和w中去掉的一重黑色,在原来是红色或黑色的x.p上增加一重额外的黑色。通过将x.p作为新节点x来重复while循环。注意到,如果通过情况1进入到情况2,则新节点x就是红黑色的,因为原来的x.p是红色的,因此,新节点x的color属性值为RED,并且在测试循环条件后循环终止。然后,在第23行处将新节点x着为(单一)黑色。
情况3:x的兄弟节点w是黑色的,w的左孩子是红色的,w的右孩子是黑色的
情况3(见RB-DELETE-FIXUP的第13-16行和图13-7(c))发生在w为黑色且其左孩子为红色,右孩子为黑色时。可以交换w和其左孩子w.left的颜色,然后对w进行右旋而不违反红黑树的性质。现在x的新节点w是一个有红色右孩子的黑色节点,这样我们就从情况3转换成了情况4。
情况4:x的兄弟节点w是黑色的,且w的右孩子是红色的
情况4(见RB-DELETE-FIXUP的第17-21行和图13-7(d))发生在节点x的兄弟节点w为黑色且w的右孩子为红色时,通过进行某些颜色修改并对x.p做一次左旋,可以去掉x的额外黑色,从而使它变为单重黑色,而且不破坏红黑树性质。将x设为设为根root后,当while循环测试其循环条件时,循环终止。
RB-DELETE-FIXUP代码实现(C)
static void rbtree_delete_fixup(rbTree *T, rbtreeNode *x)
{
rbtreeNode *w;
while(x != T->root && x->color == BLACK)//while循环中,x总是指向一个具有双重黑色的非根界节点
{
if(x == x->p->left)
{
w = x->p->right;
if(w->color == RED) //情况1:x的兄弟节点w是红色
{
w->color = BLACK;
x->p->color = RED;
left_rotate(T, x->p);
w = x->p->right;
}
if(w->left->color == BLACK && w->right->color == BLACK) //情况2:x的兄弟节点w是黑色,而且w的两个子节点都是黑色的
{
w->color = RED;
x = x->p;
}
else
{
if(w->right->color == BLACK) //情况3:x的兄弟节点w是黑色的,w的左孩子是红色的,w的右孩子是黑色的
{
w->left->color = BLACK;
w->color = RED;
right_rotate(T, w);
w = x->p->right;
}
w->color = x->p->color; //情况4:x的兄弟节点w是黑色的,且w的右孩子是红色的
x->p->color = BLACK;
w->right->color = BLACK;
left_rotate(T, x->p);
x = T->root;
}
}
else//x = x->p->right
{
w = x->p->left;
if(w->color == RED)
{
w->color = BLACK;
x->p->color = RED;
right_rotate(T, x->p);
w = x->p->left;
}
if(w->left->color == BLACK && w->right->color == BLACK)
{
w->color = RED;
x = x->p;
}
else
{
if(w->left->color == BLACK)
{
w->right->color = BLACK;
w->color = RED;
left_rotate(T, w);
w = x->p->left;
}
w->color = x->p->color;
x->p->color = BLACK;
w->left->color = BLACK;
right_rotate(T, x->p);
x = T->root;
}
}
}
x->color = BLACK;
}删除分析:
参考资料:
1、《算法导论》第13章 红黑树
2、《数据结构与算法分析基础》-C语言描述
3、完整的工程代码实现见:http://download.csdn.net/detail/u012796139/8673483