深度学习笔记（七）：正则化

正则化

在上次笔记中，提到了过拟合，如何解决过拟合呢，其中正则化就是常见的减少过拟合的方法。其中常见的两种正则化方法分别是L2和L1正则化。

L2正则化

定义及公式介绍

L2正则化又叫做weight decay（权重下降），顾名思义，让神经网络尽可能学习比较小的权重。

拿之前的损失函数:交叉熵(cross-entropy)来举例子，原始的交叉熵损失函数公式和经过L2正则化后的cross-entropy公式如下(1)(2)：

$$C=-\frac{1}{n}\sum _{xj}[y_j\ln a_j^L+(1-y_j)\ln (1-a_j^L)].\text{\hspace{1em}(1)}$$
$$C=-\frac{1}{n}\sum _{xj}[y_j\ln a_j^L+(1-y_j)\ln (1-a_j^L)]+\frac{\lambda }{2n}\sum _w{w}^2.\text{\hspace{1em}(2)}$$

可以发现，我们在原来的损失函数添加了一项$\frac{\lambda }{2n}{\sum }_w{w}^2$ ,也就是加上了神经网络所有权重的平方和乘上$\frac{\lambda }{2n}$。
其中λ是一个大于0的数，n表示训练集包含实例个数

对于二次损失函数,我们也可以使用类似的方法进行L2正则化，原始函数和正则化后的函数分别如公式(3)(4):
$$C=\frac{1}{2n}\sum _x\Vert y-a^L{\Vert }^2\text{\hspace{1em}(3)}$$
$$C=\frac{1}{2n}\sum _x\Vert y-a^L{\Vert }^2+\frac{\lambda }{2n}\sum _w{w}^2.\text{\hspace{1em}(4)}$$

所以L2正则化就是对损失函数添加一项：
$$C=C_0+\frac{\lambda }{2n}\sum _w{w}^2\text{\hspace{1em}(5)}$$
其中$C_0$为原始的损失函数，$\frac{\lambda }{2n}{\sum }_w{w}^2$为L2正则化项。

因为我们神经网络的学习是为了降低损失函数Cost(最小化Cost)，所有从公式可以看出，添加正则化项偏向让神经网络学习更小的权重（因为我们已经把权重的平方和当做Cost函数的一部分了）。
可以看出公式中的$\lambda$是调整公式中的$C_0$和$\frac{\lambda }{2n}{\sum }_w{w}^2$这两项的比重,当$\lambda$比较小的时候，倾向于让$C_0$最小化,$\lambda$比较大的时候倾向于使权重之和最小化。

对于公式（5），对权重和偏向分别求偏导:
$$\frac{\partial C}{\partial w}=\frac{\partial C_0}{\partial w}+\frac{\lambda }{n}w\text{\hspace{1em}(6)}$$
$$\frac{\partial C}{\partial b}=\frac{\partial C_0}{\partial b}.\text{\hspace{1em}(7)}$$
对于单个输入实例，可以发现对偏向求偏导与之前更新法则没有区别。而权重的更新法则发生了改变:
$$w\to w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda }{n}w=\left(1-\frac{\eta \lambda }{n}\right)w-\eta \frac{\partial C_0}{\partial w}.\text{\hspace{1em}(8)}$$

权重更新公式的第一项多乘了$(1-\frac{\eta \lambda }{n})$,这是一个小于1大于0的数，相当于把$w$缩小了。

注意我们选择$\lambda$的值跟训练集实例的个数有关，当我们增加训练集实例个数，我们也需要相应的增加$\lambda$的值

实验

隐藏层: 30个神经元, mini-batch size: 10, 学习率: 0.5,损失函数使用 cross-entropy

>>> import mnist_loader 
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper() 
>>> import network2 
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000], 400, 10, 0.5,
... evaluation_data=test_data, lmbda = 0.1,
... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True,
... monitor_training_cost=True, monitor_training_accuracy=True)

Cost函数变化情况

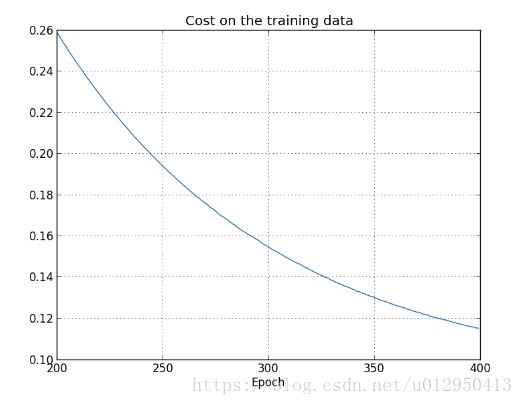
准确性的变化情况

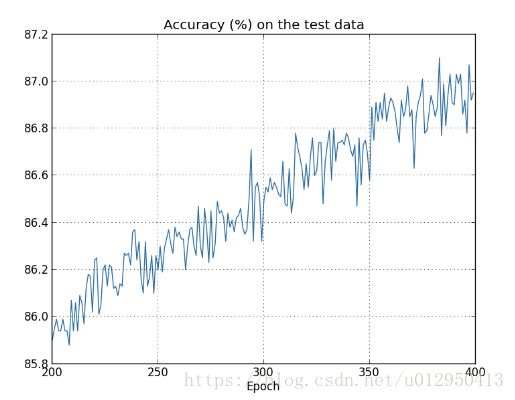
可以发现准确性一直在提高。在之前的实验中，在迭代次数变大的情况下，准确性出现不变甚至减少的情况，而添加了L2正则化项，准确性总体趋势一直在提高。

L1正则化

正则化Cost函数:
$$C=C_0+\frac{\lambda }{n}\sum _w|w|\text{\hspace{1em}(9)}$$
求偏导:
$$\frac{\partial C}{\partial w}=\frac{\partial C_0}{\partial w}+\frac{\lambda }{n}\mathrm{s}\mathrm{g}\mathrm{n}(w),\text{\hspace{1em}(10)}$$

公式中的$\mathrm{s}\mathrm{g}\mathrm{n}(\mathrm{w})$表示$w$的符号，如果是正的相当于+1,是负的相当于-1

权重的更新公式变为:
$$w\to w^{\prime }=w-\frac{\eta \lambda }{n}\mathrm{s}\mathrm{g}\mathrm{n}(\mathrm{w})-\eta \frac{\partial {\mathrm{C}}_0}{\partial \mathrm{w}},\text{\hspace{1em}(11)}$$

对比L2正则化权重更新公式:
$$w\to w^{\prime }=w\left(1-\frac{\eta \lambda }{n}\right)-\eta \frac{\partial C_0}{\partial w}.\text{\hspace{1em}(12)}$$

L1倾向于集中在少部分重要的连接上

解释:当$w=0$, 偏导数$\frac{\partial C}{\partial w}$无意义, 因为$|w|$的形状在$w=0$时是一个V字形尖锐的拐点. 所以, 当w=0时,sgn(0) = 0，相当于使用了un-regulazied表达式. 本来regularization的目的就是减小权重, 当$w=0$,无需减少。

L1和L2正则化的区别

都是减小权重, 方法不同:

1. L1减少一个常量, L2减少权重的一个固定比例
2. 如果权重本身很大, L1减少的比L2少很多
3. 如果权重本身很小, L1减少的更多

总结

正则化倾向于让神经网络学习更小的权重，输入实例X的随机变化不会对神经网络模型造成太大的影响，一些局部的噪声对神经网络的影响就比较小了，减少overfitting发生的概率。