前言
根据Gcssloop所学习的自定义View整理与笔记。
贝塞尔曲线的主要优点是可以实时控制曲线状态，一些复杂的运动状态、实时计算变化的曲线等均可使用贝塞尔曲线。
一.贝塞尔曲线初识
1. 贝塞尔曲线是由一系列点来控制曲线状态的
- 数据点 确定曲线的起始和结束位置
- 控制点 确定曲线的弯曲程度
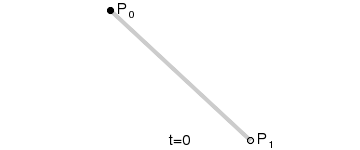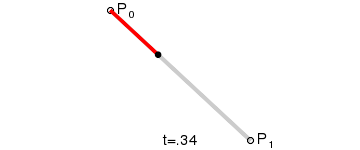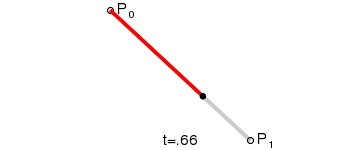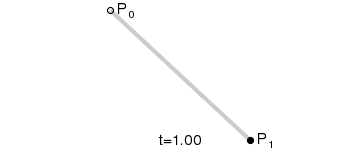
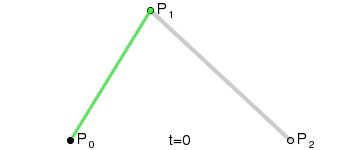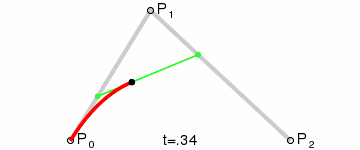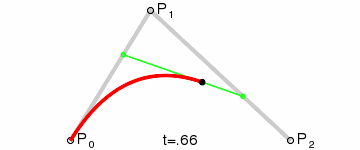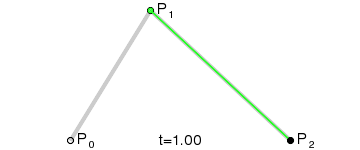
2. 一阶曲线
一阶曲线没有控制点，仅有两个数据点（P0,P1），一阶曲线就像是一条由P0至P1的直线。一阶曲线其实就是前面讲解过的lineTo
引用自维基百科
当t=0.25时，B（t）即一条由点P0至P1路径的四分之一处
公式如下：
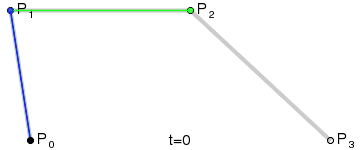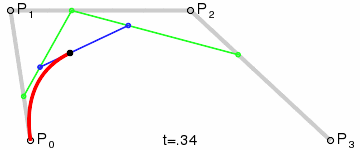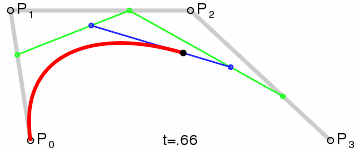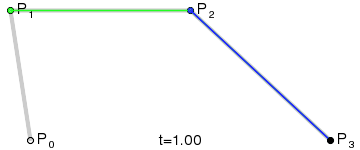
3.二阶曲线
二阶曲线由两个数据点(A 和 C)，一个控制点(B)来描述曲线状态 。 二阶曲线对应的方法是quadTo
二阶贝塞尔曲线的结构，引用自http://www.gcssloop.com/customview/Path_Bezier
此时，应满足条件：
二阶贝塞尔曲线演示动画：
二阶贝塞尔曲线演示动画
公式如下：
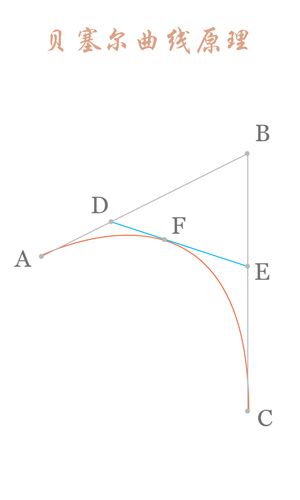
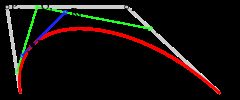
4.高阶曲线
高阶曲线计算过程与二阶类似。三阶贝塞尔曲线对应的方法是cubicTo
三阶贝塞尔曲线的结构：
引用自维基百科
三阶贝塞尔曲线的演示动画：
引用自维基百科
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是在那里提供方向资讯。P0和P1之间的间距，决定了曲线在转而趋进P2之前，走向P1方向的“长度有多长”
公式如下：
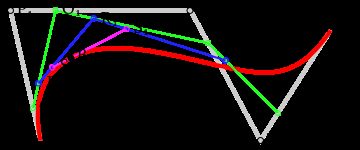
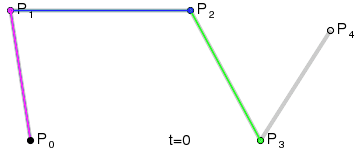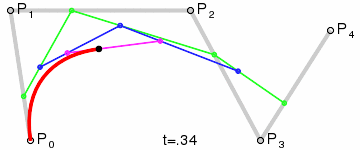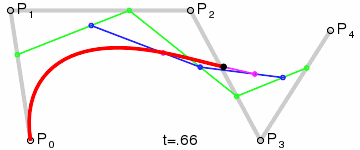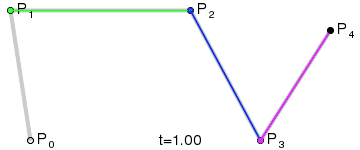
四阶的参考看一下吧，[不用的]：
四阶贝塞尔曲线：
引用自维基百科
引用自维基百科
n阶贝塞尔曲线公式：
二.贝塞尔曲线相关函数使用方法
首先，咱们用二阶曲线感受一下
demo：
public class MineView extends View {
private Paint paint;
private PointF control;//控制点
private PointF start, end;//数据点
public MineView(Context context) {
this(context, null);
}
public MineView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
paint = new Paint();
paint.setStyle(Paint.Style.STROKE);
control = new PointF(0, 0);
start = new PointF(0, 0);
end = new PointF(0, 0);
}
@Override
public boolean onTouchEvent(MotionEvent event) {
control.x = event.getX();
control.y = event.getY();
invalidate();
return true;
}
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
int centerX = w / 2;
int centerY = h / 2;
start.x = centerX - 200;
start.y = centerY;
end.x = centerX + 200;
end.y = centerY;
control.x = centerX;
control.y = centerY;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//绘制数据点
paint.setColor(Color.BLACK);
paint.setStrokeWidth(20);
canvas.drawPoint(start.x, start.y, paint);
canvas.drawPoint(end.x, end.y, paint);
//绘制辅助线
paint.setColor(Color.GRAY);
paint.setStrokeWidth(5);
canvas.drawLine(start.x, start.y, control.x, control.y, paint);
canvas.drawLine(end.x, end.y, control.x, control.y, paint);
//绘制贝塞尔曲线
paint.setColor(Color.RED);
paint.setStrokeWidth(8);
Path path = new Path();
path.moveTo(start.x, start.y);
path.quadTo(control.x, control.y, end.x, end.y);
canvas.drawPath(path, paint);
}
}
效果图如下(无法缩小了=_=，请见谅)：
一阶贝塞尔曲线demo
然后，咱们感受一下三阶曲线：
demo：
public class MineView extends View {
private Paint paint;
private PointF control, control2;//控制点
private PointF start, end;//数据点
private int changeControl;
public MineView(Context context) {
this(context, null);
}
public MineView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
public void setChangeControl(int changeControl) {
this.changeControl = changeControl;
}
private void init() {
paint = new Paint();
paint.setStyle(Paint.Style.STROKE);
control = new PointF(0, 0);
control2 = new PointF(0, 0);
start = new PointF(0, 0);
end = new PointF(0, 0);
}
@Override
public boolean onTouchEvent(MotionEvent event) {
if (changeControl == 0) {
control.x = event.getX();
control.y = event.getY();
}
else {
control2.x = event.getX();
control2.y = event.getY();
}
invalidate();
return true;
}
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
int centerX = w / 2;
int centerY = h / 2;
start.x = centerX - 200;
start.y = centerY;
end.x = centerX + 200;
end.y = centerY;
control.x = centerX;
control.y = centerY;
control2.x = centerX;
control2.y = centerY;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
paint.setColor(Color.BLACK);
paint.setStrokeWidth(20);
//绘制数据点
canvas.drawPoint(start.x, start.y, paint);
canvas.drawPoint(end.x, end.y, paint);
//绘制辅助线
paint.setColor(Color.GRAY);
paint.setStrokeWidth(5);
canvas.drawLine(start.x, start.y, control.x, control.y, paint);
canvas.drawLine(control.x, control.y, control2.x, control2.y, paint);
canvas.drawLine(end.x, end.y, control2.x, control2.y, paint);
//绘制贝塞尔曲线
paint.setColor(Color.RED);
paint.setStrokeWidth(8);
Path path = new Path();
path.moveTo(start.x, start.y);
path.cubicTo(control.x, control.y, control2.x, control2.y, end.x, end.y);
canvas.drawPath(path, paint);
}
再来一张大大的效果图~~~(>_<)~~~
三阶贝塞尔曲线效果图
后记
Gcssloop还有很多实例demo，这里便不做讲解了，大家感兴趣的，可以前去研究一下哦
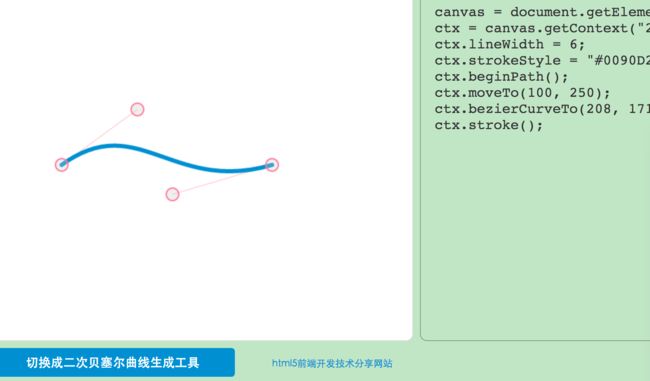
工具推荐
这里有一个贝塞尔曲线绘图工具
,大家可以用哦，大概页面是这样子的，毕竟这个控制点什么的太难算啦，至今没找到好的计算方法，如果大家有好的计算方式，求告知~~~
贝塞尔工具页面部分截图
参考网站
维基百科