simulink入门2--机器人控制系统仿真

1. 概述

详细介绍《机器人控制系统的设计与MATLAB仿真》--刘金琨 编著 的仿真程序Simulink 主程序：chap2_1sim.mdl 的仿真步骤。

2. 控制律设计

忽略在重力和外加干扰，采用独立 PD 控制，实现机器人的定点控制要求。
设 n 关节机械手方程为:
$$D(q)\ddot{q}+C(q,\dot{q})\dot{q}=\tau \text{\hspace{1em}(1)}$$
式中：D(q) 为 n×n 阶正定惯性矩阵，C(q,$\dot{q}$) 为 n×n 阶离心力和哥氏力，$\tau$为关节力矩，q 为关节角度(要实现的位置)，$\ddot{q}$为角加速度，$\dot{q}$为角速度。
独立的PD控制律为：
$$\tau =K_d\dot{e}+K_{p}e\text{\hspace{1em}(2)}$$
其中：跟踪误差为 e = q_d - q,当采用定点方式控制时，q_d 为常数项(要求机械手达到的位置)，$\dot{q}$_d = $\ddot{q}$_d = 0

3. 收敛性

由李雅普诺夫判据及 LaSalle 定理可知，(e,$\dot{e}$) = (0,0)是受控机器人全局渐进稳定的平衡点，即从任意初始条件 (q₀,$\dot{q}$₀) 出发，均有 q→q_d,$\dot{q}$_d→0.

4. 仿真实例步骤

选取二关节机械臂(不考虑重力、摩擦力和干扰)，利用拉格朗日动力学方程，求得动力学模型为：
D(q) $\ddot{q}$ + C(q,$\dot{q}$) $\dot{q}$ = $\tau$
其中：
$$D(q)=\left[\begin{array}{cc}{p}_1+p_2+2p_{3}cos{q}_2& p_2+p_{3}cos{q}_2\\ p_2+p_{3}cos{q}_2& p_2\end{array}\right]$$
$$C(q,\dot{q})=\left[\begin{array}{cc}-p_3{\dot{q}}_{2}sin{q}_2& -p_3({\dot{q}}_1+{\dot{q}}_2)sin{q}_2\\ p_3{\dot{q}}_{1}sin{q}_2& 0\end{array}\right]$$
程序中关于D(q)和C(q,$\dot{q}$)d的写法

D0=[p(1)+p(2)+2*p(3)*cos(x(3)) p(2)+p(3)*cos(x(3));
    p(2)+p(3)*cos(x(3)) p(2)];
C0=[-p(3)*x(4)*sin(x(3)) -p(3)*(x(2)+x(4))*sin(x(3));
     p(3)*x(2)*sin(x(3))  0];

取
p = [2.90   0.76   0.87   3.04   0.87]^T，
q₀ = [0 0]^T，
$\dot{q}$₀ = [0 0]^T。
关节角度位置指令为：
q_d(0) = [1 1]^T。
在控制器式（2）中，取
K_p = [100  0; 0  100],
K_d = [100  0; 0  100]。

4.1 仿真概述

详细介绍《机器人控制系统的设计与MATLAB仿真》--刘金琨 编著 的仿真程序Simulink 主程序：chap2_1sim.mdl 仿真实例的仿真步骤。

4.2 simulink窗口

4.3 新建"Blank Model",

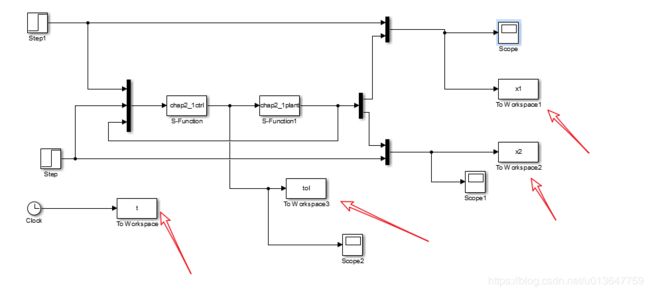
4.4 构建simulink仿真图

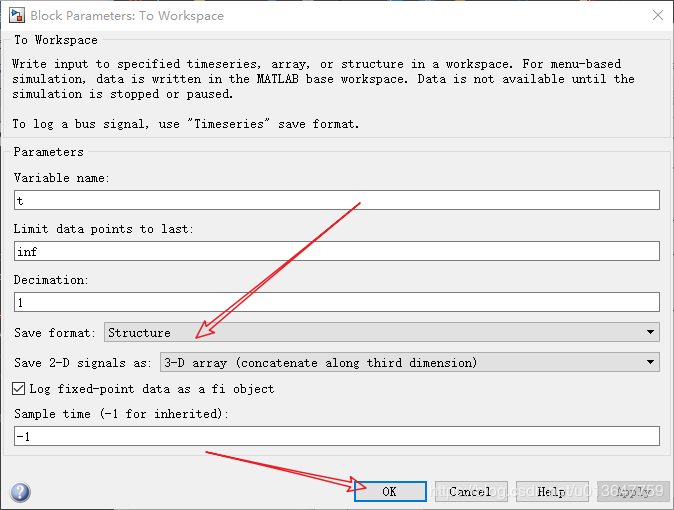
需要指出的是:position,position1,position2 是 sinks 中的 to workspace 模块.

4.4.1 注意

1. 双击t模块，将Save format更改为Structure
   
   
2. 方法如上，将 tol x1 x2的Save format均更改为Structure
   

4.4.2 关于4.4.1节内容的解释

参见如下文章：

1. 将simulink的Scope波形数据保存到workspace
2. MATLAB将simulink中波形数据输出到工作空间
3. matlab2018中simulink scope数据导出到matlab变量中；
4. matlab2018中simulink scope数据导出到matlab变量中；

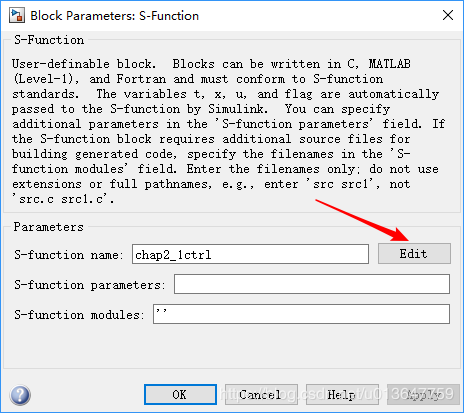
4.5 编辑第一个s函数chap2_1ctrl

• 双击 S-Function,选择 Edit,然后点击Open Editor

• 在编辑器打开后，首先选择保存，保存名为chap2_1ctrl,与simulink文件保存在同一目录下，并在编辑器中输入如下代码，然后回到Block Parameters S-Function(第4步)点击 ok
  

function [sys,x0,str,ts] = chap2_1ctrl(t,x,u,flag)
% 新定义函数 chap2_1ctrl,四个参数为 t,x,u,flag,另外 sys 是输出
% 参看 sim 仿真图，这个函数是控制器 chap2_1ctrl 控制器的函数
% 实现 τ = Kd*e + Kp*E ,其中：e 是角速度误差，E 是位置误差(2020.3.25 更新)
% 参数说明：(2020.3.25 更新)
%   x1：关节 1 的位置，其导数为其角速度
%   x2：关节 2 的位置，其导数为其角速度
%   tol:关节力矩，为 2x1 的矩阵，其中 tol(1) 为关节 1 的力矩，tol(2)同理。
% 输入输出：
%   输入：6 个输入，依次分别为 u(1),u(2),u(3),u(4),u(5),u(6)，分别对应
%        sim 图中的 step1,step2, x1 ,x1 的倒数，x2, x2 的倒数（x1, x2为实际
%        关节1，关节2 的位置，其导数则为角速度）
%   输出：tol:关节力矩，为 2x1 的矩阵，其中 tol(1) 为关节 1 的力矩，tol(2)同理。
switch flag,  % 判断flag
case 0,       % flag == 0,调用 mdlInitializeSizes 函数
    [sys,x0,str,ts]=mdlInitializeSizes;
case 3,       % flag == 3,调用 mdlOutputs 函数
    sys=mdlOutputs(t,x,u);
case {2,4,9}
    sys=[];   % 输出为空
otherwise  
    error(['Unhandled flag = ',num2str(flag)]);
end

%-------mdlInitializeSizes 函数-------------------%
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;         % 结构体模块的赋值
sizes.NumOutputs     = 2; % 输出参数为控制力矩， tol 为 2x1 的矩阵(2020.3.25 更新)
sizes.NumInputs      = 6; % 输入参数 6 个，两个 step，四个chap2_1plant的输出
sizes.DirFeedthrough = 1; % 输入直接控制输出
sizes.NumSampleTimes = 1; % 采样时间为 1
sys = simsizes(sizes);    % 确定参数赋值给 sys

x0  = [];                 % 初始值为空
str = [];                 % 默认设置为空
ts  = [0 0];              % 采样时间与偏移量


%-------mdlOutputs(t,x,u) 函数-------------------%
function sys=mdlOutputs(t,x,u)  % 函数有三个输入参数(结合sim图观察)
R1=u(1);      % step 是 u1，即前文分析的位置指令 qd(0)[1;1]的(1,1)元素
dr1=0;        % 微分，对 R1 的微分，即关节角 1 的角速度(2020.3.25 更新)
R2=u(2);      % step 是 u2，即前文分析的位置指令 qd(0)[1;1]的(1,2)元素
dr2=0;        % 微分，对 R2 的微分，即关节角 2 的角速度 (2020.3.25 更新)

x(1)=u(3);    % 状态变量，反馈环节chap2_1plant的输出作为控制器的输入x1
x(2)=u(4);    % 状态变量，反馈环节chap2_1plant的输出作为控制器的输入 x1的导数
x(3)=u(5);    % 状态变量，反馈环节chap2_1plant的输出作为控制器的输入x2
x(4)=u(6);    % 状态变量，反馈环节chap2_1plant的输出作为控制器的输入 x2的导数

e1=R1-x(1);   % 输入与输出的偏差
e2=R2-x(3);   % 输入与输出的偏差
e=[e1;e2];    % 位置偏差
 
de1=dr1-x(2); % 偏差的导数
de2=dr2-x(4); % 偏差的导数
de=[de1;de2]; % 角速度偏差

Kp=[50 0;0 50]; 
Kd=[50 0;0 50];

tol=Kp*e+Kd*de; % PD 控制，在sim中作为输出变量，输出到 workspace

sys(1)=tol(1);  % 关节 1 的驱动力矩
sys(2)=tol(2);  % 关节 2 的驱动力矩

4.6 编辑第二个s函数chap2_1plant

function [sys,x0,str,ts]=chap2_1plant(t,x,u,flag)
% S-function for continuous state equation
% 此为 sim 图中的被控对象 char2_1plant 的函数
switch flag,  % 判断 flag
%Initialization
  case 0,     % flag == 0，执行 mdlInitializeSizes 子函数
    [sys,x0,str,ts]=mdlInitializeSizes;
case 1,       % flag == 2，执行 mdlDerivatives 子函数
    sys=mdlDerivatives(t,x,u);
%Outputs
  case 3,% flag == 3，执行 mdlOutputs 子函数
    sys=mdlOutputs(t,x,u);
%Unhandled flags
  case {2, 4, 9 }
    sys = [];
%Unexpected flags
  otherwise
    error(['Unhandled flag = ',num2str(flag)]);
end

%-------mdlInitializeSizes 函数-------------------%
function [sys,x0,str,ts]=mdlInitializeSizes
global p g                  % 定义全局变量 p g 
sizes = simsizes;
sizes.NumContStates  = 4;   % 连续变量 4 个
sizes.NumDiscStates  = 0;   % 离散变量 0 个
sizes.NumOutputs     = 4;   % 输出 4 个
sizes.NumInputs      =2;    % 输入 2 个
sizes.DirFeedthrough = 0;   % 输入不控制输出
sizes.NumSampleTimes = 0;   % 采样时间为 0，被控对象,无需采样
sys=simsizes(sizes);
x0=[0 0 0 0];
str=[];
ts=[];

p=[2.9 0.76 0.87 3.04 0.87];  % p 是D(q)正定惯性矩阵的各项系数
g=9.8;      % 重力系数 9.8

%-------mdlDerivatives 函数-------------------%
function sys=mdlDerivatives(t,x,u)
global p g  
D0=[p(1)+p(2)+2*p(3)*cos(x(3)) p(2)+p(3)*cos(x(3));
    p(2)+p(3)*cos(x(3)) p(2)]; % 正定惯性矩阵
C0=[-p(3)*x(4)*sin(x(3)) -p(3)*(x(2)+x(4))*sin(x(3));
     p(3)*x(2)*sin(x(3))  0];  % 离心力和哥氏力
 
% 被控对象 chap2_1plant的输入是控制器的输出，此时的u(1:2)是
% chap2_1ctrl 的输出 sys,即经过 PD 调节的力矩
%
tol=u(1:2);        
dq=[x(2);x(4)];    % x1的导数，x2的导数

S=inv(D0)*(tol-C0*dq);  % 动力学方程的反向应用，用于求出角加速度
% 这里的sys 为中间变量，S(1),S(2)为关节角1，2的角加速度
sys(1)=x(2);
sys(2)=S(1);
sys(3)=x(4);
sys(4)=S(2);

%-------mdlOutputs 函数-------------------%
function sys=mdlOutputs(t,x,u)
sys(1)=x(1);  % 状态变量 x1,作为被控对象的输出，同时反馈到控制器
sys(2)=x(2);  % 状态变量 x1的导数,作为被控对象的输出，同时反馈到控制器
sys(3)=x(3);  % 状态变量 x2,作为被控对象的输出，同时反馈到控制器
sys(4)=x(4);  % 状态变量 x2的导数,作为被控对象的输出，同时反馈到控制器

4.7 新建m文件chap2_1plot

• 编辑器选择新建文件，保存为’chap2_1plot’，目录与上述文件目录相同
  
• 输入程序如下

close all;

% 绘制关节位置与关节角速度
figure(1);
subplot(211);
plot(t.signals(1).values(:,1), x1.signals(1).values(:,2),'r', ...
     t.signals(1).values(:,1), x1.signals(1).values(:,3),'b');
xlabel('time(s)');ylabel('position tracking of link 1');
subplot(212);
plot(t.signals(1).values(:,1), x2.signals(1).values(:,2),'r', ...
     t.signals(1).values(:,1), x2.signals(1).values(:,3),'b');
xlabel('time(s)');ylabel('position tracking of link 2');

% 关节力矩
figure(2);
subplot(211);
plot(t.signals(1).values(:,1), tol.signals(1).values(:,1),'r');
xlabel('time(s)');ylabel('tol1');
subplot(212);
plot(t.signals(1).values(:,1), tol.signals(1).values(:,2),'r');
xlabel('time(s)');ylabel('tol2');

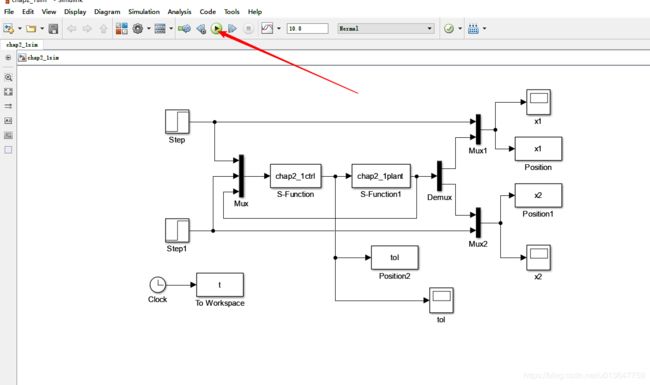
4.8 仿真

1. 在m函数编辑器处点击运行
   
2. 选择“添加到路径”
   
3. 忽略上述关于参数的提示，运行simulink(书中没有示波器，参照上文添加示波器)
   3.1 忽略下图的提示
   

3.2 运行仿真，点击示波器，观察图形：


3.3 与此同时，在matlab的工作区出现参数：

5 注意事项

1. 在搭建好simulink，完成m函数的编辑之后，首先运行m函数(忽略matlab给出的错误提示)，然后再运行simulink。分析原因：在添加到路径这一步骤中，matlab将m函数读入，从而在simulink的运行时，不会在报错(找不到函数)
2. chap2_1plant·实际输出了 4 个信号，分别为x1, x1 的导数，x2，x2 的导数。在经过一个demux分离后，x1 与 x1 的导数上行与 step1信号经过mux到达示波器，故示波器显示三根线，x2 与 x2 的导数同理与step2经mux到达示波器，示波器显示三根线。
3. simulink的搭建中，x1,x2,tol都是多个信号的混合，可以采用demux将信号分开。
4. 这本书作为入门不太好，推荐先看看《用MATLAB玩转机器人》(电子版或实体书)