朴素贝叶斯分类

朴素贝叶斯分类原理

数据挖掘课后总结一下朴素贝叶斯原理，时间久了差点儿忘，再次整理一下。
首先看要求：

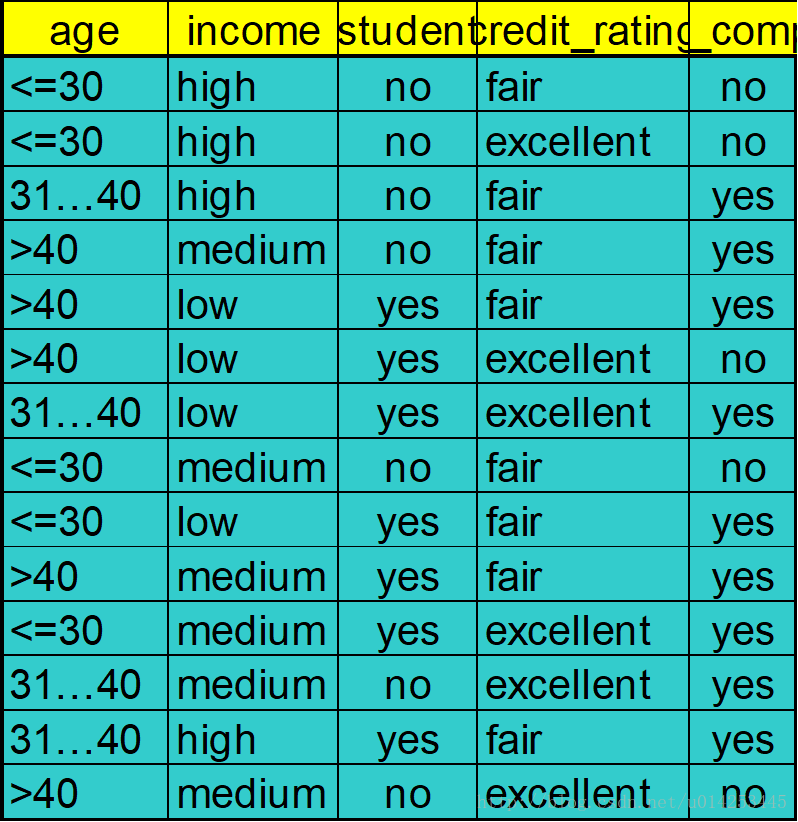
已由上述数据，现给如下数据和要求
1. Class:
C1:buys_computer = ‘yes’
C2:buys_computer = ‘no’
2. Data to be classified:
X = (age <=30, Income = medium,Student = yes，Credit_rating = Fair)

---

一、问题分析

给图表数据，是针对年龄，收入情况，是否为学生，信用评级这四个属性描述是否购买电脑。要求的是某人情况为 X（年龄<=30，收入中等，学生，信用一般）是否会买电脑。
很显然，这是分类问题，给出列表形式，现在用朴素贝叶斯来解决此问题。首先简介朴素贝叶斯的原理。

二、关于朴素贝叶斯

“朴素”何意？–条件独立性。简单认为各个属性之间都是独立的不相关的，也会有一些情况预测不准，可能属性之间并不“朴素”。那么朴素贝叶斯分类原理是什么呢？

条件概率

拿题目中的分类要求来说，可以用概率来表示P(C|X)：在X条件下，买电脑的概率是多少？如果C1表示买，C0表示不买。那么P(C1|X)>P(C0|X)就可以得出当某人满足X条件时，买电脑的概率会大些。反之，则不买。很好理解。
接下来就是要说求P(C1|X)就可以了。我们知道公式：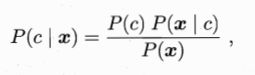
这是条件概率形式，变形有 P(C|X) * P(X) = P(X|C) * P(C) = P(X C) = P (X , C)。
其中P(C)是类先验概率，P(X|C)是样本x相对与类标记c的类条件概率，或称为似然概率；P(X)是用于归一化的证据因子，对给定样本x，证据因子P(X)与类标记无关。因此估计P(C|X)的问题，就转化为如何基于训练集数据D来估计先验概率P(C)，以及似然概率 P(X|C)。

三、求解过程

想求P(C|X)：即该人 x 情况下，会不会买电脑？因为是后验概率，所以要求P(C),P(X|C)。
P(X|C)：即买(或不买)电脑的里面符合该条件的人占多大比例

（1）求先验概率P(C)

先验概率是指根据以往经验和分析得到的概率，它往往作为“由因求果”问题中的“因”出现。
P(C1)：即买电脑的概率，数数就能算出来 9/14 = 0.643
P(C2)：不买电脑的概率，同上 5/14 = 0.357

（2）求条件概率P(X|C)

后验概率是指在得到“结果”的信息后重新修正的概率，是“执果寻因”问题中的“因” 。就是知道已经买电脑了，看看此人X的情况。

1. P(X|C1)

容易看出来X条件是有多个条件符合构成的，并且之间为条件独立。
P(X|C1)=P(age <= 30|C1)*P(income = medium|C1)*P(student = yes|C1)*P(credit_rating = fair|C1)

2. P(X|C0)

同理能得到该表达式：
P(X|C0)=P(age <= 30|C0)*P(income = medium|C0)*P(student = yes|C0)*P(credit_rating = fair|C0)

3. 可以理解为，买电脑的里面满足这四个条件是必须的。计算各条件概率为

P(age = “<=30” | C1) = 2/9 = 0.222
P(age = “<= 30” | C0) = 3/5 = 0.6
P(income = “medium” | C1) = 4/9 = 0.444
P(income = “medium” | C0) = 2/5 = 0.4
P(student = “yes” | C1) = 6/9 = 0.667
P(student = “yes” | C0) = 1/5 = 0.2
P(credit_rating = fair | C1) = 6/9 = 0.667
P(credit_rating = fair| C0) = 2/5 = 0.4

4. 得到各式结果后，就能计算得出：P(X | C1)，P(X | C0)的概率

P(X|C1)=0.222 * 0.444 * 0.667 *0.667 = 0.044
P(X|C0)=0.6 * 0.4 * 0.2 * 0.4 = 0.019

5. 再计算 P(X,C1) P(X,C0)。可以忽略P(X)证据因子

P(X|C1) * P(C1) = 0.044 * 0.643 = 0.028
P(X|C0) * P(C0) = 0.019 * 0.357 = 0.007

6. 显然，当某人条件为X时，买电脑的概率会更大。

备注：

很多情况下，很多代码中计算到P(X|C) * P(C)就可以分类了。（周志华一书：事实上，很多机器学习技术无需准确估计出后验概率P(C|X)，也就是最终结果，就可以准确进行分类了）。看公式，求得P(X , C1)与P(X, C2)比较大小即可，因为同除以P(X)不影响二者大小，更何况本题中并没有P(X)的大小。

四、小结

记忆贝叶斯分类器，记住条件概率的公式，然后确定要求的概率，剩下的就很容易理顺下来了！注意P(X|C)=P(X1|C)*P(X2|C)*……
下图为课件，解释了所有内容……