机器学习笔记——岭回归(Ridge Regression)
本内容整理自coursera,欢迎转载交流。
(https://www.coursera.org/specializations/machine-learning)
1.一般回归遇到的问题
一般的回归模型很容易出现过拟合(overfitting)的问题。
为了说明过拟合,先介绍两个概念:
error=bias+variance
bias:指的是模型在样本上的输出与真实值的误差。
variance:指的是每个模型的输出结果与所有模型平均值(期望)之间的误差。
所以模型复杂度较低的时候bias比较大,而variance很小,模型复杂度高的时候恰好相反。
因此为了获得合适的模型,我们需要在模型对数据的拟合程度(bias)和模型复杂(variance)度之间权衡。
2.岭回归模型(Ridge Regression Model)
我们定义损失函数:
Total cost=mesaure of fit+measure of magnitude of coefficients =RSS(w^)+λ|w^|2
我们该怎么确定 λ 呢?先来讨论一下以下情况:
λ=0 :这时候相当于令 RSS 最小,和之前介绍的最小二乘法一样;
λ=+∞ :这时候如果 |w^|=0 ,那么 w^ 是 0⃗ ,否则total coat无穷大。
λ 介于0~无穷大,我们可以通过数学方法求得最小值。
有上面的讨论我们可以知道, λ 为大值时,bias很大,variance很小;否则相反。
3.岭回归的求解
在前面的博客里,我们已经知道: RSS(w⃗ )=(y⃗ −H⃗ w⃗ )T(y⃗ −H⃗ w⃗ )
Total cost=(y⃗ −H⃗ w⃗ )T(y⃗ −H⃗ w⃗ )+λw⃗ Tw⃗
下面不加证明的给出 ΔTotal cost=−2H⃗ T(y⃗ −H⃗ w⃗ )+2w⃗
3.1数学描述法
令 ΔTotal cost=0 ,化简得到:
−H⃗ T(y⃗ −H⃗ w⃗ )+λI⃗ w⃗ =0w⃗ ridge=(H⃗ TH⃗ +λI⃗ )−1H⃗ Ty⃗
3.2梯度下降法(Gradient Descent)
w(t+1)j←wtj−ηΔTotal cost
化简:
w(t+1)j←(1−2ηλ)wtj+2η∑Ni=1hj(xi)(yi−yi(w^))
4.K折交叉验证(k-fold cross validation)
当数据量比较小的时候,我们可能没有足够的数据分为training set,validation set, test set。
我们可以先把数据分为training set和test set,然后我们把training set均分为K份,交叉验证的步骤如下:
for k=1, 2, 3 … … , K:
每次选择第k个作为validation set,其余的作为training set,拟合得到 w⃗ (k)
计算拟合模型在validation的误差 errork(λ)
完成循环后计算平均误差: CV(λ)=1K∑K(k=1)errork(λ)
选择CV最小的确定我们需要的λ。
K一般选取5或者10
5.如何处理截距
Total cost=(y⃗ −H⃗ w⃗ )T(y⃗ −H⃗ w⃗ )+λw⃗ Tw⃗ =RSS(w⃗ )+λ|w⃗ |2
最小化上述公式的结果是我们也希望 w0 也是很小的,也就是说我们希望截距很小,但是我们真的需要截距小吗?试问,我们拟合很多数据,可能这些数据在零点附近并没有观测值,我们需要要求我们的拟合曲线有一个小截距吗?答案是不需要。因此,我们需要单独考虑常数特征。
5.1 Option 1
我们可以这样:
RSS(w0,wrest)+λ|w⃗ rest|22
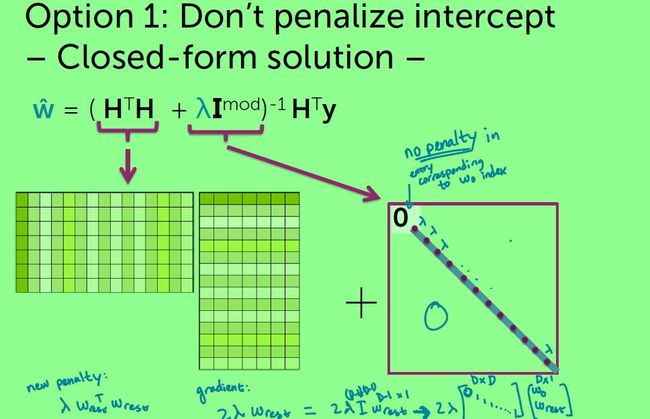
用梯度下降法可以如下表示:
当 |ΔRSS(w⃗ t)|>ϵ
for j=0,...,D:
partial[j]=−2∑Ni=1hj(xi)(yi−y^i(w⃗ t))
if j==0
w(t+1)0←wt0−η⋅partial[j]
else
w(t+1)j←(1−2ηλ)wtj−η⋅partial[j]
t←t+1
5.2 Option 2
设想如果我们的Y值均值约为0,那么我们要求截距小的话就很合理,所以我们可以先把我们所有的y值平移使之均值为0,然后就可以按照原来的方法求解了,是不是很有趣?
6. 代码实现岭回归
本部分内容代码和数据文件可以在这里下载。
以下代码分别是使用graphlab实现岭回归和使用自己编写的梯度下降算法实现岭回归。
#先使用graphlab实现,体会结果
import graphlab
#实现获得对应的数据并转换化为numpy格式
def polynomial_sframe(feature, degree):
poly_sframe = graphlab.SFrame()
# and set poly_sframe['power_1'] equal to the passed feature
poly_sframe['power_1'] = feature
# first check if degree > 1
if degree > 1:
# then loop over the remaining degrees:
# range usually starts at 0 and stops at the endpoint-1. We want it to start at 2 and stop at degree
for power in range(2, degree+1):
# first we'll give the column a name:
name = 'power_' + str(power)
# then assign poly_sframe[name] to the appropriate power of feature
poly_sframe[name] = poly_sframe['power_1'].apply(lambda x:x**power)
return poly_sframe
import matplotlib.pyplot as plt
%matplotlib inline
sales = graphlab.SFrame('kc_house_data.gl/')
sales = sales.sort(['sqft_living','price'])
l2_small_penalty = 1e-5
poly15_data = polynomial_sframe(sales['sqft_living'], 15)
featuresme=poly15_data.column_names()
poly15_data['price'] = sales['price']
model15degree = graphlab.linear_regression.create(poly15_data, target='price', features=featuresme,validation_set=None, verbose=False,l2_penalty=l2_small_penalty)
print model15degree.coefficients.print_rows(num_rows=16)
#把数据分为四个集合分别拟合
(semi_split1, semi_split2) = sales.random_split(.5,seed=0)
(set_1, set_2) = semi_split1.random_split(0.5, seed=0)
(set_3, set_4) = semi_split2.random_split(0.5, seed=0)
data1 = polynomial_sframe(set_1['sqft_living'],15)
f1=data1.column_names()
data1['price'] = set_1['price']
mymodel1 = graphlab.linear_regression.create(data1, target='price', features=f1,validation_set=None, verbose=False,l2_penalty=l2_small_penalty)
plt.plot(data1['power_1'],data1['price'],'.',data1['power_1'],mymodel1.predict(data1),'-')
print mymodel1.coefficients.print_rows(num_rows=16)
data2 = polynomial_sframe(set_2['sqft_living'],15)
f2=data2.column_names()
data2['price'] = set_2['price']
mymodel2 = graphlab.linear_regression.create(data2, target='price', features=f2,validation_set=None, verbose=False,l2_penalty=l2_small_penalty)
plt.plot(data2['power_1'],data2['price'],'.',data2['power_1'],mymodel2.predict(data2),'-')
print mymodel2.coefficients.print_rows()
data3 = polynomial_sframe(set_3['sqft_living'],15)
f3=data3.column_names()
data3['price'] = set_3['price']
mymodel3 = graphlab.linear_regression.create(data3, target='price', features=f3,validation_set=None, verbose=False,l2_penalty=l2_small_penalty)
plt.plot(data3['power_1'],data3['price'],'.',data3['power_1'],mymodel3.predict(data3),'-')
print mymodel3.coefficients.print_rows()
data4 = polynomial_sframe(set_4['sqft_living'],15)
f4=data4.column_names()
data4['price'] = set_4['price']
mymodel4 = graphlab.linear_regression.create(data4, target='price', features=f4,validation_set=None, verbose=False,l2_penalty=l2_small_penalty)
plt.plot(data4['power_1'],data4['price'],'.',data4['power_1'],mymodel4.predict(data4),'-')
print mymodel4.coefficients.print_rows()
"""
Ridge regression comes to rescue
Generally, whenever we see weights change so much in response to change in data, we believe the variance of our estimate to be large. Ridge regression aims to address this issue by penalizing "large" weights. (Weights of model15 looked quite small, but they are not that small because 'sqft_living' input is in the order of thousands.)
With the argument l2_penalty=1e5, fit a 15th-order polynomial model on set_1, set_2, set_3, and set_4. Other than the change in the l2_penalty parameter, the code should be the same as the experiment above. Also, make sure GraphLab Create doesn't create its own validation set by using the option validation_set = None in this call.
"""
data1 = polynomial_sframe(set_1['sqft_living'],15)
l2_small_penalty = 1e5
f1=data1.column_names()
data1['price'] = set_1['price']
mymodel1 = graphlab.linear_regression.create(data1, target='price', features=f1,validation_set=None, verbose=False,l2_penalty=l2_small_penalty)
plt.plot(data1['power_1'],data1['price'],'.',data1['power_1'],mymodel1.predict(data1),'-')
print mymodel1.coefficients.print_rows(num_rows=16)
data2 = polynomial_sframe(set_2['sqft_living'],15)
f2=data2.column_names()
data2['price'] = set_2['price']
mymodel2 = graphlab.linear_regression.create(data2, target='price', features=f2,validation_set=None, verbose=False,l2_penalty=l2_small_penalty)
plt.plot(data2['power_1'],data2['price'],'.',data2['power_1'],mymodel2.predict(data2),'-')
print mymodel2.coefficients.print_rows()
data3 = polynomial_sframe(set_3['sqft_living'],15)
f3=data3.column_names()
data3['price'] = set_3['price']
mymodel3 = graphlab.linear_regression.create(data3, target='price', features=f3,validation_set=None, verbose=False,l2_penalty=l2_small_penalty)
plt.plot(data3['power_1'],data3['price'],'.',data3['power_1'],mymodel3.predict(data3),'-')
print mymodel3.coefficients.print_rows()
data4 = polynomial_sframe(set_4['sqft_living'],15)
f4=data4.column_names()
data4['price'] = set_4['price']
mymodel4 = graphlab.linear_regression.create(data4, target='price', features=f4,validation_set=None, verbose=False,l2_penalty=l2_small_penalty)
plt.plot(data4['power_1'],data4['price'],'.',data4['power_1'],mymodel4.predict(data4),'-')
print mymodel4.coefficients.print_rows()
"""
Selecting an L2 penalty via cross-validation
Just like the polynomial degree, the L2 penalty is a "magic" parameter we need to select. We could use the validation set approach as we did in the last module, but that approach has a major disadvantage: it leaves fewer observations available for training. Cross-validation seeks to overcome this issue by using all of the training set in a smart way.
We will implement a kind of cross-validation called k-fold cross-validation. The method gets its name because it involves dividing the training set into k segments of roughtly equal size. Similar to the validation set method, we measure the validation error with one of the segments designated as the validation set. The major difference is that we repeat the process k times as follows:
Set aside segment 0 as the validation set, and fit a model on rest of data, and evalutate it on this validation set
Set aside segment 1 as the validation set, and fit a model on rest of data, and evalutate it on this validation set
...
Set aside segment k-1 as the validation set, and fit a model on rest of data, and evalutate it on this validation set
After this process, we compute the average of the k validation errors, and use it as an estimate of the generalization error. Notice that all observations are used for both training and validation, as we iterate over segments of data.
To estimate the generalization error well, it is crucial to shuffle the training data before dividing them into segments. GraphLab Create has a utility function for shuffling a given SFrame. We reserve 10% of the data as the test set and shuffle the remainder. (Make sure to use seed=1 to get consistent answer.)
"""
(train_valid, test) = sales.random_split(.9, seed=1)
train_valid_shuffled = graphlab.toolkits.cross_validation.shuffle(train_valid, random_seed=1)
first = train_valid_shuffled[0:5818]
second = train_valid_shuffled[7758:len(train_valid_shuffled)]
train4 = first.append(second)
"""
Now we are ready to implement k-fold cross-validation. Write a function that computes k validation errors by designating each of the k segments as the validation set. It accepts as parameters (i) k, (ii) l2_penalty, (iii) dataframe, (iv) name of output column (e.g. price) and (v) list of feature names. The function returns the average validation error using k segments as validation sets.
For each i in [0, 1, ..., k-1]:
Compute starting and ending indices of segment i and call 'start' and 'end'
Form validation set by taking a slice (start:end+1) from the data.
Form training set by appending slice (end+1:n) to the end of slice (0:start).
Train a linear model using training set just formed, with a given l2_penalty
Compute validation error using validation set just formed
"""
def k_fold_cross_validation(k, l2_penalty, data, output_name, features_list):
n = len(data)
RSS=0
for i in range(k):
start = n*i/k
end = n*(i+1)/k
validation_set = data[start:end]
first_t = data[0:start]
second_t = data[end:n]
train_set = first_t.append(second_t)
model = graphlab.linear_regression.create(train_set, target=output_name, features=features_list,l2_penalty=l2_penalty, validation_set=None,verbose=False)
predicted = model.predict(validation_set)
err = predicted-validation_set[output_name]
RSS += (err*err).sum()
Rss = RSS/k
return Rss
"""
Once we have a function to compute the average validation error for a model, we can write a loop to find the model that minimizes the average validation error. Write a loop that does the following:
We will again be aiming to fit a 15th-order polynomial model using the sqft_living input
For l2_penalty in [10^1, 10^1.5, 10^2, 10^2.5, ..., 10^7] (to get this in Python, you can use this Numpy function: np.logspace(1, 7, num=13).)
Run 10-fold cross-validation with l2_penalty
Report which L2 penalty produced the lowest average validation error.
Note: since the degree of the polynomial is now fixed to 15, to make things faster, you should generate polynomial features in advance and re-use them throughout the loop. Make sure to use train_valid_shuffled when generating polynomial features!
"""
import numpy as np
validata = polynomial_sframe(train_valid_shuffled['sqft_living'],15)
featuremy = validata.column_names()
validata['price'] = train_valid_shuffled['price']
penalty = np.logspace(1,7,num=13)
for pen in penalty:
rss = k_fold_cross_validation(10, pen, validata, 'price', featuremy)
print rss
data = polynomial_sframe(train_valid_shuffled['sqft_living'], 15)
features = data.column_names()
data['price'] = train_valid_shuffled['price']
model_last = graphlab.linear_regression.create(data, target='price', features=features, validation_set=None,verbose=False,l2_penalty=penalty[4])
pre = model_last.predict(test)
err = pre-test['price']
rss = (err*err).sum()
print rss#下面是自己编写梯度下降算法实现岭回归,体会算法
# coding: utf-8
## Regression Week 4: Ridge Regression (gradient descent)
# In this notebook, you will implement ridge regression via gradient descent. You will:
# * Convert an SFrame into a Numpy array
# * Write a Numpy function to compute the derivative of the regression weights with respect to a single feature
# * Write gradient descent function to compute the regression weights given an initial weight vector, step size, tolerance, and L2 penalty
import graphlab
sales = graphlab.SFrame('kc_house_data.gl/')
import numpy as np # note this allows us to refer to numpy as np instead
def get_numpy_data(data_sframe, features, output):
data_sframe['constant'] = 1
features = ['constant'] + features
features_sframe = data_sframe[features]
feature_matrix = features_sframe.to_numpy()
output_sarray = data_sframe[output]
output_sarray = output_sarray.to_numpy()
return (feature_matrix, output_sarray)
#预测函数
def predict_output(feature_matrix, weights):
predictions = np.dot(feature_matrix,weights)
return(predictions)
## Computing the Derivative
# We are now going to move to computing the derivative of the regression cost function. Recall that the cost function is the sum over the data points of the squared difference between an observed output and a predicted output, plus the L2 penalty term.
# ```
# Cost(w)
# = SUM[ (prediction - output)^2 ]
# + l2_penalty*(w[0]^2 + w[1]^2 + ... + w[k]^2).
# Since the derivative of a sum is the sum of the derivatives, we can take the derivative of the first part (the RSS) as we did in the notebook for the unregularized case in Week 2 and add the derivative of the regularization part. As we saw, the derivative of the RSS with respect to `w[i]` can be written as:
# 2*SUM[ error*[feature_i] ].
# The derivative of the regularization term with respect to `w[i]` is:
# 2*l2_penalty*w[i].
# Summing both, we get
# 2*SUM[ error*[feature_i] ] + 2*l2_penalty*w[i].
# That is, the derivative for the weight for feature i is the sum (over data points) of 2 times the product of the error and the feature itself, plus `2*l2_penalty*w[i]`.
# **We will not regularize the constant.** Thus, in the case of the constant, the derivative is just twice the sum of the errors (without the `2*l2_penalty*w[0]` term).
# Recall that twice the sum of the product of two vectors is just twice the dot product of the two vectors. Therefore the derivative for the weight for feature_i is just two times the dot product between the values of feature_i and the current errors, plus `2*l2_penalty*w[i]`.
# With this in mind complete the following derivative function which computes the derivative of the weight given the value of the feature (over all data points) and the errors (over all data points). To decide when to we are dealing with the constant (so we don't regularize it) we added the extra parameter to the call `feature_is_constant` which you should set to `True` when computing the derivative of the constant and `False` otherwise.
def feature_derivative_ridge(errors, feature, weight, l2_penalty, feature_is_constant):
# If feature_is_constant is True, derivative is twice the dot product of errors and feature
if feature_is_constant == True:
derivative = 2*np.dot(errors,feature)
# Otherwise, derivative is twice the dot product plus 2*l2_penalty*weight
else:
derivative = 2*np.dot(errors,feature)+2*l2_penalty*weight
return derivative
## Gradient Descent
# Now we will write a function that performs a gradient descent. The basic premise is simple. Given a starting point we update the current weights by moving in the negative gradient direction. Recall that the gradient is the direction of *increase* and therefore the negative gradient is the direction of *decrease* and we're trying to *minimize* a cost function.
# The amount by which we move in the negative gradient *direction* is called the 'step size'. We stop when we are 'sufficiently close' to the optimum. Unlike in Week 2, this time we will set a **maximum number of iterations** and take gradient steps until we reach this maximum number. If no maximum number is supplied, the maximum should be set 100 by default. (Use default parameter values in Python.)
# With this in mind, complete the following gradient descent function below using your derivative function above. For each step in the gradient descent, we update the weight for each feature before computing our stopping criteria.
def ridge_regression_gradient_descent(feature_matrix, output, initial_weights, step_size, l2_penalty, max_iterations=100):
print 'Starting gradient descent with l2_penalty = ' + str(l2_penalty)
weights = np.array(initial_weights) # make sure it's a numpy array
iteration = 0 # iteration counter
print_frequency = 1 # for adjusting frequency of debugging output
#while not reached maximum number of iterations:
while iteration < max_iterations:
iteration += 1 # increment iteration counter
### === code section for adjusting frequency of debugging output. ===
if iteration == 10:
print_frequency = 10
if iteration == 100:
print_frequency = 100
if iteration%print_frequency==0:
print('Iteration = ' + str(iteration))
### === end code section ===
# compute the predictions based on feature_matrix and weights using your predict_output() function
pre_out = predict_output(feature_matrix,weights)
# compute the errors as predictions - output
err = pre_out-output
# from time to time, print the value of the cost function
if iteration%print_frequency==0:
print 'Cost function = ', str(np.dot(errors,errors) + l2_penalty*(np.dot(weights,weights) - weights[0]**2))
for i in xrange(len(weights)): # loop over each weight
# Recall that feature_matrix[:,i] is the feature column associated with weights[i]
# compute the derivative for weight[i].
#(Remember: when i=0, you are computing the derivative of the constant!)
if i ==0:
weights[i] = weights[i] - step_size*feature_derivative_ridge(err, feature_matrix[:,i], weights[i], l2_penalty, True)
# subtract the step size times the derivative from the current weight
else:
weights[i] = (1-2*step_size*l2_penalty)*weights[i] - 2*step_size*np.dot(feature_matrix[:,i],err)
print 'Done with gradient descent at iteration ', iteration
print 'Learned weights = ', str(weights)
return weights
# Let us split the dataset into training set and test set. Make sure to use `seed=0`:
train_data,test_data = sales.random_split(.8,seed=0)
# In this part, we will only use `'sqft_living'` to predict `'price'`. Use the `get_numpy_data` function to get a Numpy versions of your data with only this feature, for both the `train_data` and the `test_data`.
(simple_feature_matrix, output) = get_numpy_data(train_data, simple_features, my_output)
(simple_test_feature_matrix, test_output) = get_numpy_data(test_data, simple_features, my_output)
initial_weights = np.array([0., 0.])
step_size = 1e-12
max_iterations=1000
# First, let's consider no regularization. Set the `l2_penalty` to `0.0` and run your ridge regression algorithm to learn the weights of your model. Call your weights:`simple_weights_0_penalty`
simple_weights_0_penalty = ridge_regression_gradient_descent(simple_feature_matrix, output, initial_weights, step_size, 0.0, max_iterations)
# Next, let's consider high regularization. Set the `l2_penalty` to `1e11` and run your ridge regression algorithm to learn the weights of your model. Call your weights:`simple_weights_high_penalty`
simple_weights_high_penalty = ridge_regression_gradient_descent(simple_feature_matrix, output, initial_weights, step_size, 1e11, max_iterations)
import matplotlib.pyplot as plt
get_ipython().magic(u'matplotlib inline')
plt.plot(simple_feature_matrix,output,'k.',
simple_feature_matrix,predict_output(simple_feature_matrix, simple_weights_0_penalty),'b-',
simple_feature_matrix,predict_output(simple_feature_matrix, simple_weights_high_penalty),'r-')
# Compute the RSS on the TEST data for the following three sets of weights:
# 1. The initial weights (all zeros)
# 2. The weights learned with no regularization
# 3. The weights learned with high regularization
# Which weights perform best?
pre1 = predict_output(simple_test_feature_matrix,initial_weights)
err1 = pre1 - test_output
rss1 = (err1*err1).sum()
print rss1
pre1 = predict_output(simple_test_feature_matrix,simple_weights_0_penalty)
err1 = pre1 - test_output
rss1 = (err1*err1).sum()
print rss1
pre1 = predict_output(simple_test_feature_matrix,simple_weights_high_penalty)
err1 = pre1 - test_output
rss1 = (err1*err1).sum()
print rss1
print initial_weights,simple_weights_0_penalty,simple_weights_high_penalty
# ***QUIZ QUESTIONS***
# 1. What is the value of the coefficient for `sqft_living` that you learned with no regularization, rounded to 1 decimal place? What about the one with high regularization?
# 2. Comparing the lines you fit with the with no regularization versus high regularization, which one is steeper?
# 3. What are the RSS on the test data for each of the set of weights above (initial, no regularization, high regularization)?
## Running a multiple regression with L2 penalty
model_features = ['sqft_living', 'sqft_living15'] # sqft_living15 is the average squarefeet for the nearest 15 neighbors.
my_output = 'price'
(feature_matrix, output) = get_numpy_data(train_data, model_features, my_output)
(test_feature_matrix, test_output) = get_numpy_data(test_data, model_features, my_output)
initial_weights = np.array([0.0,0.0,0.0])
step_size = 1e-12
max_iterations = 1000
# First, let's consider no regularization. Set the `l2_penalty` to `0.0` and run your ridge regression algorithm to learn the weights of your model. Call your weight `multiple_weights_0_penalty`
multiple_weights_0_penalty = ridge_regression_gradient_descent(feature_matrix, output, initial_weights, step_size, 0.0, max_iterations)
# Next, let's consider high regularization. Set the `l2_penalty` to `1e11` and run your ridge regression algorithm to learn the weights of your model. Call your weights:`multiple_weights_high_penalty`
multiple_weights_high_penalty = ridge_regression_gradient_descent(feature_matrix,output, initial_weights,step_size, 1e11, max_iterations)
# Compute the RSS on the TEST data for the following three sets of weights:
# 1. The initial weights (all zeros)
# 2. The weights learned with no regularization
# 3. The weights learned with high regularization
pre = predict_output(test_feature_matrix,initial_weights)
err = pre - test_output
rss = (err*err).sum()
print rss
pre = predict_output(test_feature_matrix,multiple_weights_0_penalty)
err = pre - test_output
rss = (err*err).sum()
print rss
pre = predict_output(test_feature_matrix,multiple_weights_high_penalty)
err = pre - test_output
rss = (err*err).sum()
print rss
print initial_weights,multiple_weights_0_penalty,multiple_weights_high_penalty
# Predict the house price for the 1st house in the test set using the no regularization and high regularization models. (Remember that python starts indexing from 0.) How far is the prediction from the actual price? Which weights perform best for the 1st house?
p1 = predict_output(test_feature_matrix[0],multiple_weights_0_penalty)
print p1
p2=predict_output(test_feature_matrix[0],multiple_weights_high_penalty)
print p2
print test_output[0]
# ***QUIZ QUESTIONS***
# 1. What is the value of the coefficient for `sqft_living` that you learned with no regularization, rounded to 1 decimal place? What about the one with high regularization?
# 2. What are the RSS on the test data for each of the set of weights above (initial, no regularization, high regularization)?
# 3. We make prediction for the first house in the test set using two sets of weights (no regularization vs high regularization). Which weights make better prediction for that particular house?