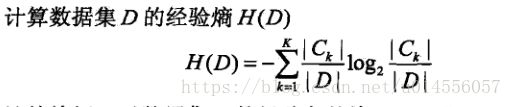机器学习--决策树python实现案例
注:文中相关截图或内容取自《统计学习方法》李航编
简介:
决策树(decision tree)是基本的分类与回归方法。对分类和回归的理解,通俗的讲就是最终结果是离散的为分类任务,结果是连续的是回归任务。决策树中每个非叶节点用一个(多个)特征进行选择向下探索的分支(每个节点相当于“switch 特征i:”的语句或者多个if 、else if的组合),最后探索至叶节点将实例判定为其分类。
如图为关于是否批准贷款的简单决策树:
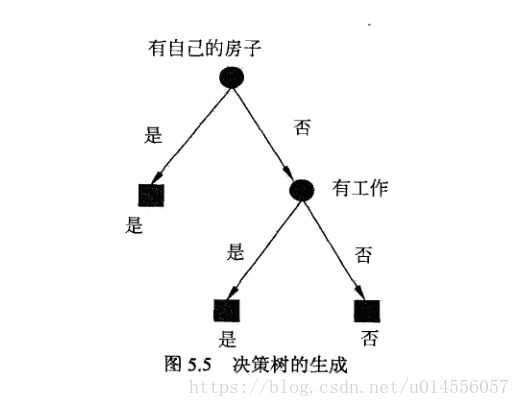
决策树中节点的分支数根据该节点所选取的特征的值域确定。
信息增益
1.熵
在节点的特征选择上,需要现了解熵、条件熵和信息增益的概念。当前节点的划分特征选择信息增益最大的特征。

其中pi=训练集中该特征值为xi的样本的数量 / 总数。熵越大,随机变量的不确定性越大。
2.条件熵

pij = 在类yi的样本集中该特征值为xi的样本的数量 / 类yi的样本数量
3.信息增益
生成决策树的步骤
案例:
下面通过一个实例来实现这个算法。
项目数据下载及说明,如下链接:
http://archive.ics.uci.edu/ml/datasets/Car+Evaluation
请自行下载数据,以及了解数据的相关内容。
数据样例:
Class Values:
unacc, acc, good, vgood
Attributes:
buying: vhigh, high, med, low.
maint: vhigh, high, med, low.
doors: 2, 3, 4, 5more.
persons: 2, 4, more.
lug_boot: small, med, big.
safety: low, med, high.
样本:
vhigh,vhigh,2,2,small,low,unacc
vhigh,vhigh,2,2,small,med,unacc
vhigh,vhigh,2,2,small,high,unacc
vhigh,vhigh,2,2,med,low,unacc
vhigh,vhigh,2,2,med,med,unacc
vhigh,vhigh,2,2,med,high,unacc
,,,
…
…
代码实现
部分函数
1、载入数据,抽象数据特征
#从文档中读取数据,每条数据转成列表的形式
def readData(path):
dataList = []
with open(path,'r') as f:
dataSet = f.readlines()
for d in dataSet:
d = d[:-1]
d = d.split(',')
dataList.append(d)
return dataList
#映射属性值,方便代码处理
Cls = {'unacc':0, 'acc':1, 'good':2, 'vgood':3} #分类值映射
#特征值映射,共6个特征值,每个特征表示为X[i],X[i][xiv]表示特征Xi的取值。
X = [{'vhigh':0, 'high':1, 'med':2, 'low':3},
{'vhigh':0, 'high':1, 'med':2, 'low':3},
{'2':0, '3':1, '4':2, '5more':3},
{'2':0, '4':1, 'more':2},
{'small':0, 'med':1, 'big':2},
{'low':0, 'med':1, 'high':2}]
2、 计算熵
def CountEachClass(dataSet):
numEachClass = [0]*len(Cls) #列表初始化
for d in dataSet:
numEachClass[Cls[d[-1]]] +=1
return numEachClass
def caculateEntropy(dataSet):
NumEachClass = CountEachClass(dataSet)
dataNum = len(dataSet)
ent = 0
for numC in NumEachClass:
temp = numC/dataNum
if(temp != 0):
ent -= temp * log(temp,2)
return ent
3、 计算每个特征的信息增益,选择信息增益最大的特征作为划分子树集的依据
def calGain(dataset,xi): #计算信息增益
res = 0
ent = caculateEntropy(dataset)
subDataSet = splitData(dataset,xi)
for xivDataSet in subDataSet:
if(xivDataSet):
res += len(xivDataSet)/len(dataset) * caculateEntropy(xivDataSet)
return ent - res
def getMaxGain(dataSet,usedX=[]): #获得最大的信息增益值和对应的特征序号
gains = []
for xi in range(len(X)):
if(xi not in usedX):
gains.append(calGain(dataSet,xi))
else:
gains.append(0)
mg = max(gains)
mx = gains.index(mg)
return mx,mg
def splitData(dataSet,xi):
subDataSets = [ [] for i in range(len(X[xi]))] #子数据集列表初始化
for d in dataSet:
subDataSets[ X[xi][d[xi]] ].append(d)
return subDataSets
4、递归构建决策树
def createTree(dataSet,r,usedX=[]): #以字典的结构构建决策树
if (len(dataSet)==0):
return {} #空树
tree = {}
numEachClass = CountEachClass(dataSet)
c = numEachClass.index(max(numEachClass))
tree['class'] = c #该树各分类中数据最多的类,记为该根节点的分类
mx,mg = getMaxGain(dataSet,usedX)
print("max gain:",mg)
if len(usedX) == len(X) or numEachClass[c] == len(dataSet) or mg < r:
tree['factureX'] = -1 #不在继续分支,即为叶节点
return tree
else:
tree['factureX']= mx #记录该根节点用于划分的特征
subDataSet = splitData(dataSet, mx) #用该特征的值划分子集,用于构建子树
for xiv in range(len(X[mx])):
xivDataSet = subDataSet[xiv]
newusedX = usedX.copy()
newusedX.append(mx)
tree[xiv] = createTree(xivDataSet,r,newusedX)
return tree
5、给样本分类
def classify(tree,data):
xi = tree['factureX'] #根节点用于划分子树的特征
if(xi>=0):
subtree = tree[X[xi][data[xi]]]
if subtree=={}: #节点没有该子树
return tree['class'] #以该节点的分类作为数据的分类
return classify(subtree,data) #否则遍历子树
else: #叶节点
return tree['class']
完整代码
from math import log
import numpy as np
#从文档中读取数据,每条数据转成列表的形式
def readData(path):
dataList = []
with open(path,'r') as f:
dataSet = f.readlines()
for d in dataSet:
d = d[:-1]
d = d.split(',')
dataList.append(d)
return dataList
#将数据集划分为训练集和测试集
def splitTestData(dataList,testnum):
trainData = []
testData = []
dataNum = len(dataList)
pred_ind = np.random.randint(0,dataNum,testnum)
for d in pred_ind:
testData.append(dataList[d])
for d in range(dataNum):
if d not in pred_ind:
trainData.append(dataList[d])
print("dataSetNum:",dataNum,len(trainData),len(testData))
return trainData,testData
#映射属性值,方便代码处理
Cls = {'unacc':0, 'acc':1, 'good':2, 'vgood':3} #分类值映射
#特征值映射,共6个特征值,每个特征表示为X[i],X[i][xiv]表示特征Xi的取值。
X = [{'vhigh':0, 'high':1, 'med':2, 'low':3},
{'vhigh':0, 'high':1, 'med':2, 'low':3},
{'2':0, '3':1, '4':2, '5more':3},
{'2':0, '4':1, 'more':2},
{'small':0, 'med':1, 'big':2},
{'low':0, 'med':1, 'high':2}]
def CountEachClass(dataSet):
numEachClass = [0]*len(Cls) #列表初始化
for d in dataSet:
numEachClass[Cls[d[-1]]] +=1
return numEachClass
def caculateEntropy(dataSet):
NumEachClass = CountEachClass(dataSet)
dataNum = len(dataSet)
ent = 0
for numC in NumEachClass:
temp = numC/dataNum
if(temp != 0):
ent -= temp * log(temp,2)
return ent
def splitData(dataSet,xi):
subDataSets = [ [] for i in range(len(X[xi]))] #子数据集列表初始化
for d in dataSet:
subDataSets[ X[xi][d[xi]] ].append(d)
return subDataSets
def calGain(dataset,xi): #计算信息增益
res = 0
ent = caculateEntropy(dataset)
subDataSet = splitData(dataset,xi)
for xivDataSet in subDataSet:
if(xivDataSet):
res += len(xivDataSet)/len(dataset) * caculateEntropy(xivDataSet)
return ent - res
def getMaxGain(dataSet,usedX=[]): #获得最大的信息增益值和对应的特征序号
gains = []
for xi in range(len(X)):
if(xi not in usedX):
gains.append(calGain(dataSet,xi))
else:
gains.append(0)
mg = max(gains)
mx = gains.index(mg)
return mx,mg
def createTree(dataSet,r,usedX=[]): #以字典的结构构建决策树
if (len(dataSet)==0):
return {} #空树
tree = {}
numEachClass = CountEachClass(dataSet)
c = numEachClass.index(max(numEachClass))
tree['class'] = c #该树各分类中数据最多的类,记为该根节点的分类
mx,mg = getMaxGain(dataSet,usedX)
print("max gain:",mg)
if len(usedX) == len(X) or numEachClass[c] == len(dataSet) or mg < r:
tree['factureX'] = -1 #不在继续分支,即为叶节点
return tree
else:
tree['factureX']= mx #记录该根节点用于划分的特征
subDataSet = splitData(dataSet, mx) #用该特征的值划分子集,用于构建子树
for xiv in range(len(X[mx])):
xivDataSet = subDataSet[xiv]
newusedX = usedX.copy()
newusedX.append(mx)
tree[xiv] = createTree(xivDataSet,r,newusedX)
return tree
def classify(tree,data):
xi = tree['factureX'] #根节点用于划分子树的特征
if(xi>=0):
subtree = tree[X[xi][data[xi]]]
if subtree=={}: #节点没有该子树
return tree['class'] #以该节点的分类作为数据的分类
return classify(subtree,data) #否则遍历子树
else: #叶节点
return tree['class']
#测试:
testNum = 100
err = 0
right = 0
dataSet = readData('car.data.txt')
trainDataSet,testDataSet = splitTestData(dataSet,testNum)
tree = createTree(trainDataSet,0.2)
for d in testDataSet:
c = classify(tree,d)
if c ==Cls[d[-1]]:
right +=1
else:
err +=1
print("分类:",c)
print('实际分类',Cls[d[-1]])
print("err:",err,"right:",right)
print("total:",testNum)
print("错误率:",err/testNum)运行结果:
...
...
分类: 0
实际分类 0
分类: 1
实际分类 1
err: 3 right: 97
total: 100
错误率: 0.03