Java实现常见的查找算法--二叉树
参考:https://blog.csdn.net/smile_from_2015/article/details/72190562?utm_source=gold_browser_extension
二叉排序树
目标是插入和查找同样高效
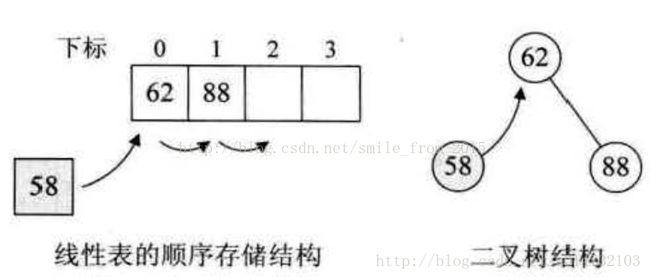
假设我们的数据集开始只有一个数{62}, 然后现在需要将88插入数据集,于是数据集成了{62,88},还保持着从小到大有序。再查找有没有58,没有则插入,可此时要想在线性表的顺序存储中有序,就得移动 62 和
88 的位置,如下左图,可不可以不移动呢?那就需要使用二叉树结构。当我们用二叉树的方式时,首先我们将第一个数62定为根结点,88因为比62大,因此让它做62的右子树,58因比62小,所以成为它的左子树。此时58的插入并没有影响到62与88的关系,如下右图所示。
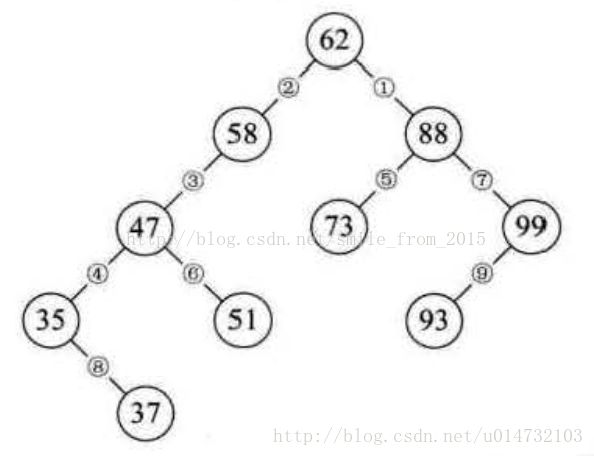
也就是说, 若我们现在需要对集合{62,88,58,47,35,73,51,99,37,93}做查找,在我们打算创建此集合时就考虑用二叉树结构,而且是排好序的二叉树来创建。如下图所示,62、88、58创建好后,下一个数 47 因比58小,是它的左子树(见③),35是47的左子树(见④),73比62大,但却比88小,是88的左子树(见⑤),51比62小、比58小、比47大,是 47的右子树(见⑥),99比62、88都大,是它的右子树(见⑦),37比62、58、47都小,但却比35大,是35的右子树(见③) ,93则因比62、88大是99的左子树(见⑨)。
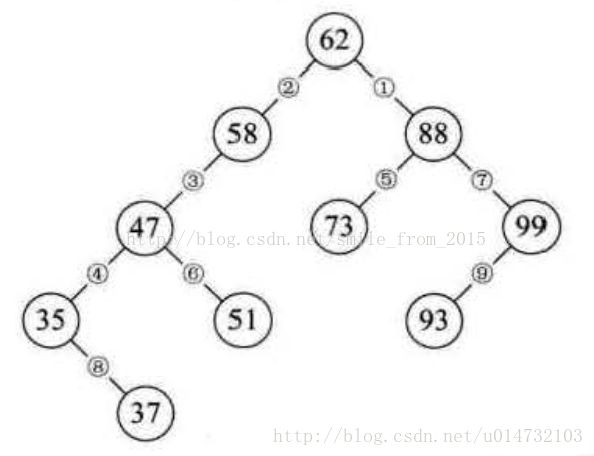
这样我们就得到了一棵二叉树,并且当我们对它进行中序遍历时,就可以得到一个有序的序列{35,37,47,51,58,62,73,88,93,99},所以我们通常称它为二叉排序树。
二叉排序树(Binary Sort Tree),又称为二叉查找树。它或者是一棵空树,或者是具有下列性质的二叉树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空 ,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树。
从二叉排序树的定义也可以知道,它前提是二叉树,然后它采用了递归的定义方法,再者,它的结点间满足一定的次序关系,左子树结点一定比其双亲结点小,右子树结点一定比其双亲结点大。
构造一棵二叉排序树的目的,其实并不是为了排序,而是为了提高查找和插入删除关键字的速度。不管怎么说,在一个有序数据集上的查找,速度总是要快于无序的数据集的,而二叉排序树这种非线性的结构,也有利于插入和删除的实现。
二叉排序树查找操作
首先我们提供一个二叉树的结构。
/**
* 二叉树,数据结构
*
*/
private static class BinaryTree {
int data;
BinaryTree lchild;
BinaryTree rchild;
}然后我们来看看二叉排序树的查找是如何实现的
public class BinarySearchTree {
public static void main(String[] args) {
// 主要是表达查询,所以手动构造一棵二叉排序树
BinaryTree binaryTree1 = new BinaryTree();
binaryTree1.data = 62;
BinaryTree binaryTree2 = new BinaryTree();
binaryTree1.lchild = binaryTree2;
binaryTree2.data = 58;
BinaryTree binaryTree3 = new BinaryTree();
binaryTree2.lchild = binaryTree3;
binaryTree3.data = 47;
BinaryTree binaryTree4 = new BinaryTree();
binaryTree3.lchild = binaryTree4;
binaryTree4.data = 35;
BinaryTree binaryTree5 = new BinaryTree();
binaryTree4.rchild = binaryTree5;
binaryTree5.data = 37;
BinaryTree binaryTree6 = new BinaryTree();
binaryTree3.rchild = binaryTree6;
binaryTree6.data = 51;
BinaryTree binaryTree7 = new BinaryTree();
binaryTree1.rchild = binaryTree7;
binaryTree7.data = 88;
BinaryTree binaryTree8 = new BinaryTree();
binaryTree7.lchild = binaryTree8;
binaryTree8.data = 73;
BinaryTree binaryTree9 = new BinaryTree();
binaryTree7.rchild = binaryTree9;
binaryTree9.data = 99;
BinaryTree binaryTree10 = new BinaryTree();
binaryTree9.lchild = binaryTree10;
binaryTree10.data = 93;
boolean search = serachBinaryTree(binaryTree1, 37, null);
System.out.println(search == true ? "查找成功" + parentNode.data : "查找失败");
}
/**
* 全局变量,存放查找到的关键字所在的父节点
*/
static BinaryTree parentNode = new BinaryTree();
/**
* 二叉排序树
*
* @param bt
* 待查询的二叉排序树
* @param key
* 查找关键字
* @param parent
* 指向bt的双亲,其初始调用值为null
* @return 查找成功返回true,并将树节点赋值给全局变量result,查找失败返回false
*/
public static boolean serachBinaryTree(BinaryTree bt, int key, BinaryTree parent) {
if (bt == null || bt.data == 0) { // 树节点不存在,返回
parentNode = parent;
return false;
} else if (key == bt.data) { // 查找成功
parentNode = bt;
return true;
} else if (key < bt.data) { // 关键字小于根节点查找左子树
return serachBinaryTree(bt.lchild, key, bt);
} else { // 关键字大于根节点查找右子树
return serachBinaryTree(bt.rchild, key, parent);
}
}
/**
* 二叉树,数据结构
*
*/
private static class BinaryTree {
int data;
BinaryTree lchild;
BinaryTree rchild;
}
}
二叉排序树插入操作
有了二叉排序树的查找函数,那么所谓的二叉排序树的插入,其实也就是将关键字放到树中的合适位置而已,来看代码。
package com.wzl.binary;
public class BinarySearchTree {
public static void main(String[] args) {
// 主要是表达查询,所以手动构造一棵二叉排序树
BinaryTree binaryTree1 = new BinaryTree();
binaryTree1.data = 62;
BinaryTree binaryTree2 = new BinaryTree();
binaryTree1.lchild = binaryTree2;
binaryTree2.data = 58;
BinaryTree binaryTree3 = new BinaryTree();
binaryTree2.lchild = binaryTree3;
binaryTree3.data = 47;
BinaryTree binaryTree4 = new BinaryTree();
binaryTree3.lchild = binaryTree4;
binaryTree4.data = 35;
BinaryTree binaryTree5 = new BinaryTree();
binaryTree4.rchild = binaryTree5;
binaryTree5.data = 37;
BinaryTree binaryTree6 = new BinaryTree();
binaryTree3.rchild = binaryTree6;
binaryTree6.data = 51;
BinaryTree binaryTree7 = new BinaryTree();
binaryTree1.rchild = binaryTree7;
binaryTree7.data = 88;
BinaryTree binaryTree8 = new BinaryTree();
binaryTree7.lchild = binaryTree8;
binaryTree8.data = 73;
BinaryTree binaryTree9 = new BinaryTree();
binaryTree7.rchild = binaryTree9;
binaryTree9.data = 99;
BinaryTree binaryTree10 = new BinaryTree();
binaryTree9.lchild = binaryTree10;
binaryTree10.data = 93;
insertBinaryTree(binaryTree1, 68);
}
/**
* 全局变量,存放查找到的关键字所在的父节点
*/
static BinaryTree parentNode = new BinaryTree();
/**
* 二叉排序树
*
* @param bt
* 待查询的二叉排序树
* @param key
* 查找关键字
* @param parent
* 指向bt的双亲,其初始调用值为null
* @return 查找成功返回true,并将树节点赋值给全局变量result,查找失败返回false
*/
public static boolean serachBinaryTree(BinaryTree bt, int key, BinaryTree parent) {
if (bt == null || bt.data == 0) { // 树节点不存在,返回
parentNode = parent;
return false;
} else if (key == bt.data) { // 查找成功
parentNode = bt;
return true;
} else if (key < bt.data) { // 关键字小于根节点查找左子树
return serachBinaryTree(bt.lchild, key, bt);
} else { // 关键字大于根节点查找右子树
return serachBinaryTree(bt.rchild, key, parent);
}
}
/**
* 在二叉树中插入关键字key
*
* @param bt
* 二叉排序树
* @param key
* 插入的关键字
* @return 插入成功返回true,失败返回false
*/
public static boolean insertBinaryTree(BinaryTree bt, int key) {
BinaryTree binaryTree;
if (!serachBinaryTree(bt, key, null)) {
binaryTree = new BinaryTree();
binaryTree.data = key;
binaryTree.lchild = binaryTree.rchild = null;
if (null == parentNode) {// 不存在,证明是父节点,将binaryTree指向bt成为新的根节点
bt = binaryTree;
} else if (key < parentNode.data) { // 当key小于子根节点,插入为左孩子
parentNode.lchild = binaryTree;
} else { // 当key大于子根节点,插入为右孩子
parentNode.rchild = binaryTree;
}
preOrderTraverse(bt);
return true;
} else {
System.out.println("该节点已存在");
}
return false;
}
/**
* 中序遍历打印线索二叉树
*
* @param t
*/
static void preOrderTraverse(BinaryTree t) {
if (null == t || t.data == 0) {
return;
}
if (t.lchild != null) {
preOrderTraverse(t.lchild); // 中序遍历左子树
}
if (t.data != 0) {
System.out.println("[" + t.data + "]"); // 显示当前节点的数据
}
if (t.rchild != null) {
preOrderTraverse(t.rchild); // 最后遍历右子树
}
}
/**
* 二叉树,数据结构
*
*/
private static class BinaryTree {
int data;
BinaryTree lchild;
BinaryTree rchild;
}
}有了二叉排序树的插入代码,我们要实现二叉排序树的构建就非常容易了。下面的代码就可以创建一棵如下图所示的树。
package com.wzl.binary;
public class BinarySearchTree {
public static void main(String[] args) {
int[] a = { 62, 88, 58, 47, 35, 73, 51, 99, 37, 93 };
for (int i = 0; i < a.length; i++) {
System.out.println("第" + i+"次");
generateBinaryTree(a[i]);
}
}
static BinaryTree newTree = new BinaryTree();
/**
* 全局变量,存放查找到的关键字所在的父节点
*/
static BinaryTree parentNode = new BinaryTree();
/**
* 二叉排序树
*
* @param bt
* 待查询的二叉排序树
* @param key
* 查找关键字
* @param parent
* 指向bt的双亲,其初始调用值为null
* @return 查找成功返回true,并将树节点赋值给全局变量result,查找失败返回false
*/
public static boolean serachBinaryTree(BinaryTree bt, int key, BinaryTree parent) {
if (bt == null || bt.data == 0) { // 树节点不存在,返回
parentNode = parent;
return false;
} else if (key == bt.data) { // 查找成功
parentNode = bt;
return true;
} else if (key < bt.data) { // 关键字小于根节点查找左子树
return serachBinaryTree(bt.lchild, key, bt);
} else { // 关键字大于根节点查找右子树
return serachBinaryTree(bt.rchild, key, parent);
}
}
/**
* 生成二叉树
* @param key
* @return
*/
public static boolean generateBinaryTree(int key) {
BinaryTree binaryTree;
if (!serachBinaryTree(newTree, key, null)) {
binaryTree = new BinaryTree();
binaryTree.data = key;
binaryTree.lchild = binaryTree.rchild = null;
if (null == parentNode) {// 不存在,证明是父节点,将binaryTree指向bt成为新的根节点
newTree = binaryTree;
} else if (key < parentNode.data) { // 当key小于子根节点,插入为左孩子
parentNode.lchild = binaryTree;
} else { // 当key大于子根节点,插入为右孩子
parentNode.rchild = binaryTree;
}
preOrderTraverse(newTree);
return true;
} else {
System.out.println("该节点已存在");
}
return false;
}
/**
* 中序遍历打印线索二叉树
*
* @param t
*/
static void preOrderTraverse(BinaryTree t) {
if (null == t || t.data == 0) {
return;
}
if (t.lchild != null) {
preOrderTraverse(t.lchild); // 中序遍历左子树
}
if (t.data != 0) {
System.out.println("[" + t.data + "]"); // 显示当前节点的数据
}
if (t.rchild != null) {
preOrderTraverse(t.rchild); // 最后遍历右子树
}
}
/**
* 二叉树,数据结构
*
*/
private static class BinaryTree {
int data;
BinaryTree lchild;
BinaryTree rchild;
}
}