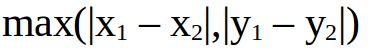“神经网络与机器学习”学习札记1：数理基础

        最近我在通过阅读学习刘凡平等编著的《神经网络与深度学习应用实战》，有一些概念比较陌生或私以为比较重要，就摘录到此，供大家学习用。

        严正声明：所有内容除特殊声明均摘自参考文献。我也已经通过邮件询问了刘凡平先生的意见，他表示只要注明出处即可。

图1 邮件咨询刘凡平先生

 

图2 刘凡平先生给予的答复

 

        有一些比较简单的概念，譬如：向量、矩阵、导数等就不一一罗列了，我只选择一些个人觉得比较陌生的内容摘录到此。

        克罗内克积：

        克罗内克积表示任意两个矩阵之间的积运算，用符号⊗表示。倘若矩阵A为p*q的一个矩阵，B为任意矩阵，则矩阵A和矩阵B的克罗内克积如下列公式所示：

 

        下面举例说明（来自百度百科，侵删！）：

 

 

        克罗内克积与数值乘法的结合律很相似，例如A、B、C为三个任意矩阵，则有以下规律：

        （1）A⊗(B+C)=A⊗B+A⊗C

        （2）(A+B)⊗C=A⊗C+B⊗C

        （3）(kA)⊗B=A⊗(kB)=k(A⊗B)

        （4）(A⊗B)⊗C=A⊗(B⊗C)

        但是克罗内克积不满足数值乘法的交换律，在一般情况下A⊗B≠B⊗A。

        除此之外，克罗内克积还有部分混合乘积的性质，例如矩阵A、B、C、D，且矩阵乘积AC和BD均存在，则(A⊗B)(C⊗D)=AC⊗BD。

        对于转置运算克罗内克积也满足，公式如下：

        距离：

        （1）欧氏距离（Eucliden Metric）。大家耳熟能详，在此不再赘述。

        （2）马氏距离（Mahalanobis Distance）。马氏距离是由印度统计学家马哈拉诺比斯提出的一种表示数值协方差距离的概念。这种协方差距离体现的是数据样本分布的距离。与欧式距离不同的是，它考虑到各种特性之间的联系，并且是尺度无关的，即独立于测量尺度。马氏距离可用于计算两个位置样本信息集合的相似度分析。

        （3）曼哈顿距离（Manhattan Distance）。曼哈顿距离是由十九世纪的赫尔曼·闵可夫斯基所创的一个词汇，是一种使用在几何度量空间的几何学用语，用以表明两个点在标准坐标系上的绝对轴距总和。它表示的不是两点间的直线距离，而是实际上从A点到达B点的距离。

        对于二维平面两点a(x1,y1) b(x2,y2)间的曼哈顿距离为：

 

        （4）切比雪夫距离（Chebyshev Distance）。切比雪夫距离是向量空间中的一种距离，两个点之间的距离定义为其各坐标数值差的最大值。以(x1,y1)和(x2,y2)两点为例，其切比雪夫距离如下所示：

 

切比雪夫距离得名自俄罗斯数学家切比雪夫。对于两个n维的变量a(p1,p2,...,pn)与变量b(q1,q2,...,qn)之间的切比雪夫距离如下：

 

        （5）闵式距离（Minkowshki Distance）。即作闵可夫斯基距离。对于两个n维的变量a(x1,x2,...,xn)与变量b(y1,y2,...,yn)之间的闵可夫斯基距离的定义如下所示，其中p是一个变参：

 

        当上述公式中p = 1时，实质上就是曼哈顿距离；当p = 2时，则是欧式空间中的一种测度，被看作是欧氏距离的一种推广，欧式距离是闵可夫斯基距离zhongp等于2的一种特殊情况；而当p趋近于无穷大时，则可视为切比雪夫距离：

 

        （6）海明距离（Hamming Distance）。在信息论中，两个等长字符串之间的海明距离是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串转变成另一个字符串时所需要替换的字符个数。

        海明重量是字符串相对于同样长度的零字符串的海明距离，也就是说，它是字符串中非零元素的个数：对于二进制字符串来说，也就是1的个数，所以11101的海明重量是4。例如，“1011111”与“1011001”之间的海明距离是2；“2243896”与“2533796”之间的海明距离是3；“beijing”与“peking”之前的海明距离是2。

        对于固定长度n，海明距离是该长度字符向量空间上的度量，很显然它满足非负、唯一与对称性，并且可以很容易地通过完全归纳法证明它满足三角不等式。两个字符a与b之间的海明距离也可看作特定运算a - b的海明距离。

        数值归一化：

        归一化（Normalization）的目的是让每一个对象在不同分类上的权值对应到区间[0,1]或[-1,1]。归一化是一种数据预处理方法，就是把需要处理的数据经过特定算法处理后，限制值区间在一定范围之内，这样做不仅是为了后面数据处理的方便，也是为了保证程序运行时加快收敛。一般常见的归一化方法如下所示。

        （1）10为底的对数函数。对数函数公式为f(x) = lg(x)。

        （2）min-max归一化。min-max归一化方法是对原始数据的线性改变，使得其结果映射在[0,1]，min表示数据集里的最小值，max表示数据集里的最大值。对于任意一个x，它的归一化公式如下：

 

        （3）z-score归一化。z-score归一化的方法借助了数据集中平均值和标准差进行计算，处理之后的数据集符合正太分布的特点，均值为0，标准差为1.对于任意的x，它的归一化公式如下，其中μ是样本均值，σ是样本的标准差：

 

 

 

 

 

 

 

 

 

 

 

 

 

参考文献：

刘凡平.神经网络与深度学习应用实战[M].北京：电子工业出版社，2018年3月.21-26.