线性表--数据结构 顺序表与链表

1.线性表的基本概念

1.1线性表的定义

线性表是一个具有相同特性数据元素的 有限 序列。
如：由n(n>=0)个数据元素(a1,a2,…,an)构成的有限的序列。
记作:L={a1,a2,…,an}

a1:表头元素
an:表尾元素

相同特性	所有元素属于同一数据类型。
有限	数据元素个数是有限的。
序列	数据元素由逻辑序号唯一确定。一个线性表中可以由相同值的元素。

线性表中所有元素的个数叫做线性表的长度，用n表示，n>=0。n=0时，表示线性表是一个空表，即表中不包含任何元素。

1.2线性表的运算

运算	描述
初始化线性表InitList(&L)	构造一个线性表L
销毁线性表Destroy(&L）	释放线性表L所占的内存空间
判断线性表是否为空表ListEmpty(L）	若L为空表，返回真，否则返回假
求线性表的长度ListLength(L)	返回L中的元素个数
输出线性表DispList(L)	线性表L不为空时，顺序显示L中各结点的值域
求线性表L中指定位置的某个元素GetElem(L,i,&e)	用e返回L中第i个元素的值
定位查找LocateElem(L,e)	返回L中第一个值域与e相等的逻辑位序。若这样的元素不存在，则返回0
插入一个数据元素ListInsert(&L,i,e)	在L的第i个元素之前插入新的元素e，L的长度增加1
删除数据元素ListDelete(&L,i,&e)	删除L的第i个元素，用e返回其值，L的长度减1

不同的存储结构的实现代码不一样，这里先不给出实现代码。
之后在具体的存储结构中给出具体代码。

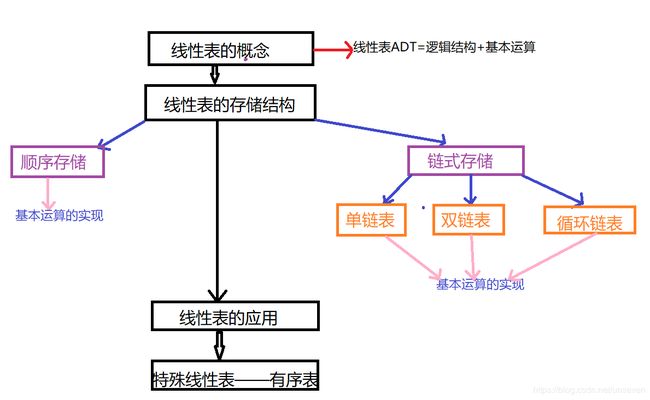
1.3线性表的知识结构

2.线性表的顺序存储结构

2.1顺序表

把线性表中的所有元素按照顺序存储结构方法进行存储。

按逻辑顺粗依次存储到一片连续的存储空间中。


顺序表类型定义：

typedef char ElemType;//假设ElemType为char
typedef struct 
{
	ElemType data[MaxSize];
   	int length;
} SqList;//顺序表类型

2.2顺序表的运算实现

1.建立顺序表
a[0…n-1]>>>顺序表L——整体创建顺序表

void CreateList(SqList L,ElemType a[],int n)
{
	int i;
	L=(SqList*)malloc(sizeof(SqList));
	for(i=0,i<n,i++)
		L->data[i]=a[i];
	L->Length=n; 
}

参数说明：
SqList *L;通过顺序表指针L操作顺序表。
SqList *&L；引用符号&放在形参L前；输出型参数均用&，不论其值是否改变。
2.初始化线性表

void InitList(Sqlist*&L)
{
	L=(SqList*)malloc(sizeof(SqLit));
	L-Length=0;
}

3.销毁线性表

void DestroyList(Sqlist *&L)
{
        free(L);
}

4.判断是否为空表

bool ListEmpty(SqList*L)
{
	return(L->length==0);//length为0，返回真，不为0，返回假 
}

5.求线性表的长度

int ListLength(SqList*L)
{
 return(L->length);
}

6.求某个数据元素的值

bool GetElem(SpList*L,int i,ElemType &e)
{
	if(i<1||i>L->length)
		return false;
	e=L->data[i-1];
	return true;
 } 

7.按元素查找

int LocateElem(SpList*L,ElemType e)
{
	int i=0;
	while(i<L->length&&L->data[i]!=e)
		i++;
	if(i>L->length) 
		return 0;
	else
		return i+1;
}

8.插入数据元素

bool ListInsert(SqList*&L,int i,ElemType e) 
{
	int i,j;
	if(i<1||i>L->length+1)//插入位置有误
		return false;
	i--;//将逻辑序号转化为物理序号，如第一个元素对应data[0] 
	for(j=L->length;j>i;j--)
		L->data[j]=L->data[j-1];//要插入元素，先把元素往后移，空出一个位置用于插入 
	L->data[i]=e; //插入元素
	L->length++;//长度加一
	return true;//插入成功 
}
//平均时间复杂度为 O(n); 

9.删除第i个元素

bool ListDelete(SqList*&L,int i,ElemType &e)
{
	int j;
	if(i<1||i>L->length)//删除位置有误 
		return false;
	i--;// 将逻辑序号转化为物理序号
	e=L->data[i];//记录删除的元素 
	for(j=i;j<L->length;j++)
		L->data[j]=L->data[j+1]; //元素前移，补齐空位
	L->length--;//长度减一
	return true;//删除成功 
}
//平均时间复杂度为 O(n);

3.线性表的链式存储结构

3.1链表

线性表中每个结点有唯一的前趋结点。
设计链式存储结构时，每个逻辑结点单独存储，为了表示逻辑关系，增加指针域。

每个物理结点增加一个指向后继结点的指针域——>单链表

每个物理结点增加一个指向后继结点的指针域和一个指向前趋结点的指针域——>双链表

为什么增加一个头结点？
1.使得第一个结点的操作与其他结点的操作相一致，否则要操作第一结点时要单独讨论。‘
2.无论链表是否为空，都有一个头结点，因此空表和非空表的处理都同一了。假如没有头结点，当为空表时又需要单独讨论。

存储密度：
指结点数据本身所占的存储量和整个结点结构所占的存储量之比

一般地，存储密度越大，存储空间利用率就越高。
顺序表的存储密度为1(100%)，而链表的存储密度小于1。

3.2单链表

单链表的结点类型LinkList的定义如下

typedef char ElemType ;//假设ElemType为char型
typedef struct LNode
{
 ElemType data;
 struct LNode *next;//指向后一个结点 
}LinkList;

1.插入和删除结点操作
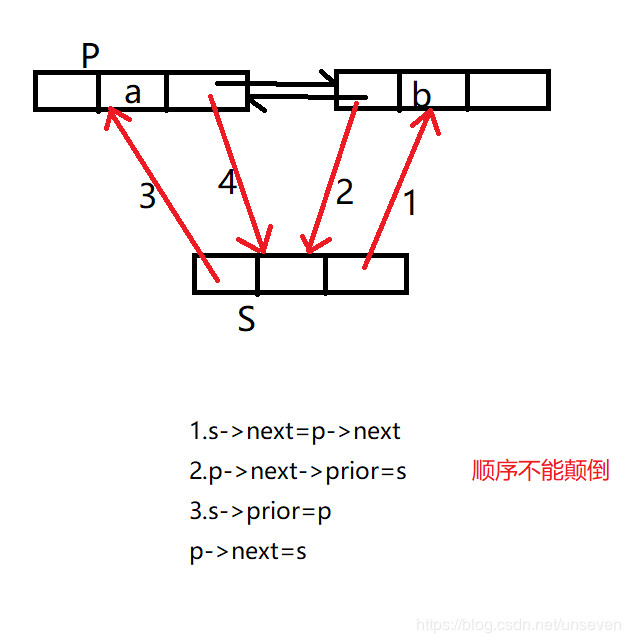
（1）插入结点
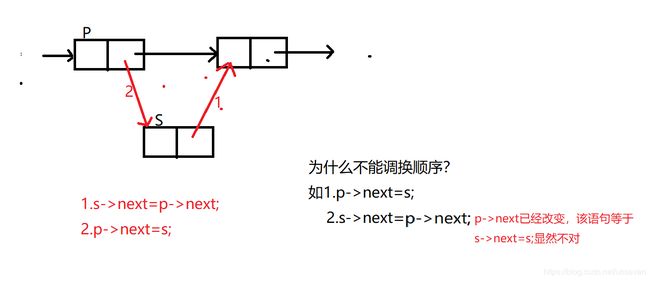特点：只需修改相关结点指针域，不需要移动过结点，节省了时间。
（2)删除结点

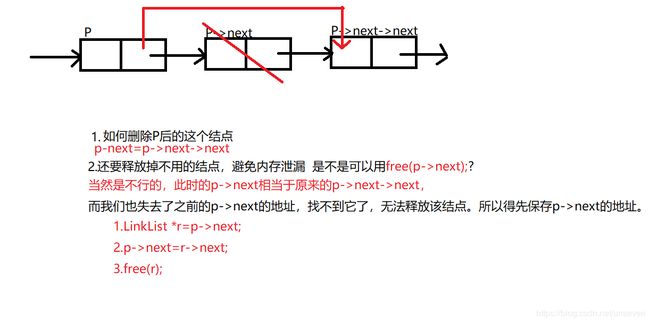
特点：只需修改相关结点的指针于，不用像顺序表一样移动结点，节省时间。

头插法建表

1.从一个空表开始，创建一个头结点
2.读取元素，生成新的结点
3.把新的结点插入到表头上
代码

void CreateListF(LinkList *&L,ElemType a[],int n)
{
	LinkList *s;
	int i;
	L=(LinkList*)malloc(sizeof(LinkList));//创建头结点 
	L->next=NULL;//头结点的指针域指向空 
	for(i=0;i<n;i++)
	{
		s=(LinkList*)malloc(sizeof(LinkList));//生成新的结点
		s->data=a[i];//从数组中取得元素
		s->next= L->next;//新的结点指向首元结点 
		L->next=s;//头结点指向新的结点，该结点变成首元结点 
	}
}

尾插法建表

1.从一个空表开始，创建一个头结点
2.读取字符数组的元素，生成新的结点
3.把新的结点插到表尾

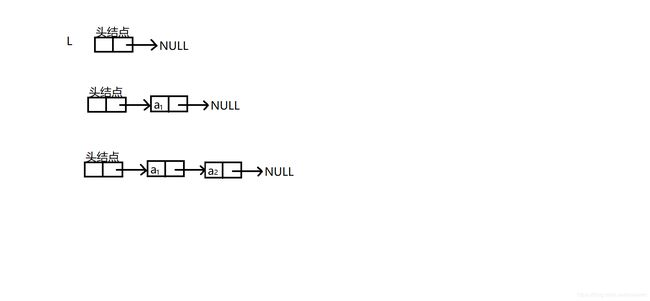
void CreateListR(LinkList *&L,ElemType a[],int n)
{
	LinkList *s,*r;
	int i;
	L=(LinkList*)malloc(sizeof(LinkList));//创建头结点 
	r=L;//r指向尾结点，开始时指向头结点，此时头结点就是尾结点
	for(i=0;i<n;i++)
	{
		s=(LinkList*)malloc(sizeof(LinkList));
		s->data=a[i];
		r->next=s;//把s插入尾部 
		r=s;//把r移到尾部 
	 } 
	r->next=NULL;//插入所有元素之后，把尾部指向空，创建完成 
 }

3.3单链表的基本算法实现

 //初始化单链表
void InitList(LinkList *&L)
{
	L=(LinkList*)malloc(sizeof(LinkList));//创建头结点
	L->next=NULL;//指向空 
 } 
 

//销毁单链表
void DestroyList(LinkList *&L)
{
	LinkList *pre=L,*p=L->next;//pre为p的前趋
	while(p!=NULL)
	{
		free(pre);//释放pre 
		pre=p;//pre后移 
		p=pre->next;//然后把p也后移，把结点一个一个释放掉 
	}	 
} 

//判断是否为空表
bool ListEmpty(LinkList *L)
{
	return (L->next==NULL);//如果头结点的下一个为空，就为空表，否则不为空 
}

//求单链表的长度
int ListLength(LinkList *L)
{
	
	int n=0;
	LinkList *p=L;//不能移动头结点的指针，不然单链表会被破坏，所以把L赋给p
	while(p->next!=NULL){
		n++;//计数
		p=p->next;//后移 
	}
	return (n); 
} 

//遍历输出 
void DisList(LinkList *L)
{
	LinkList *p=L->next;
	while(p!=NULL){
		printf("%c ",p->data);
		p=p->next;
	} 
	printf("\n");
}

//求第i个位置的元素
bool GetElem(LinkList *L,int i, ElemType &e)
{
	int j=0;
	LinkList *p=L;
	while(j<i&&p!=NULL)
	{
		j++;//计数 
		p=p->next;//找到第i个结点p 
	}
	if(p==NULL)	return false;//该节点不存在
	else{
		e=p->data;
		return true;
	}	 
}

//查找某元素的位置
int LocteElem(LinkList *L,ElemType e)
{ 
	int i=1;
	LinkList *p=L->next;
	while(p!=NULL)
	{
		p=p->next;
		i++;
	 } 
	if(p==NULL)	return (0);//该结点不存在
	else 	return (i);//返回逻辑序号 
 } 

//插入数据元素
bool ListInsert(LinkList *&L,int i,ElemType e)
{
	int j=0;
	LinkList *p=L,*s;
	while(j<i-1&&p!=NULL)
	{
		j++;
		p=p->next;//找到第i-1个结点 
	}
	if (p==NULL)	return false;//找不到 
	else{
		s=(LinkList*)malloc(sizeof(LinkList));//创建新结点 
		s->data=e;//给data赋值 
		s->next=p->next;//开始插入 
		p->next=s;//把s插入到了p之后 
		return true;
	}
 } 

//删除数据元素
bool ListDelete(LinkList *&L,int i,ElemType &e) 
{
	int j=0;
	LinkList *p=L,*q;
	while(j<i-1)
	{
		j++;
		p=p->next;//找到第i-1个结点 
	 } 
	if (p==NULL) return false;
	else{
		q=p->next;
		if(q==NULL) return false;//p已经是最后一个元素了
		e=q->data;
		p->next=q->next;
		free(q);
		return true; 
	}
}

3.4双链表

在线性表的链式存储结构中，每个物理结点增加一个指向后继结点的指针域和一个指向前趋结点的指针域——>双链表

双链表有什么优点
1.从任一结点出发可以快速找到前趋和后继结点
2.从任一结点出发可以访问到其他结点

结点类型定义：

typedef char ElemType; 
typedef struct DNode
{
	ElemType data;
	struct DNode *prior;//指向前趋 结点 
	struct Dnode *next;//指向后继结点 
}DLinkList;

插入与删除

基本操作算法实现

void InitList(DLinkList *&L)	//初始化
{
	L=(DLinkList *)malloc(sizeof(DLinkList));  	//创建头结点
	L->prior=L->next=NULL;
	L->freq=0;
}

void DestroyList(DLinkList *&L)	//销毁线性表
{
	DLinkList *p=L,*q=p->next;
	while (q!=NULL)
	{
		free(p);
		p=q;
		q=p->next;
	}
	free(p);
}

bool ListEmpty(DLinkList *L)	//判线性表是否为空表
{
	return(L->next==NULL);
}
int ListLength(DLinkList *L)	//求线性表的长度
{
	DLinkList *p=L;int i=0;
	while (p->next!=NULL)
	{
		i++;
		p=p->next;
	}
	return(i);
}

void DispList(DLinkList *L)	//输出线性表
{
	DLinkList *p=L->next;
	while (p!=NULL)
	{
		printf("%c ",p->data);
		p=p->next;
	}
	printf("\n");
}

bool GetElem(DLinkList *L,int i,ElemType &e)	//求线性表中某个数据元素值
{
	int j=0;
	DLinkList *p=L;
	while (j<i && p!=NULL)
	{
		j++;
		p=p->next;
	}
	if (p==NULL)
		return false;
	else
	{
		e=p->data;
		return true;
	}
}

int LocateElem(DLinkList *L,ElemType e)	//按元素值查找
{
	int n=1;
	DLinkList *p=L->next;
	while (p!=NULL && p->data!=e)
	{
		n++;
		p=p->next;
	}
	if (p==NULL)
		return(0);
	else
		return(n);
}

bool ListInsert(DLinkList *&L,int i,ElemType e)	//插入数据元素
{
	int j=0;
	DLinkList *p=L,*s;
	while (j<i-1 && p!=NULL)
	{
		j++;
		p=p->next;
	}
	if (p==NULL)	//未找到第i-1个结点
		return false;
	else			//找到第i-1个结点*p
	{
		s=(DLinkList *)malloc(sizeof(DLinkList));	//创建新结点*s
		s->data=e;
		s->freq=0;
		s->next=p->next;		//将*s插入到*p之后
		if (p->next!=NULL) p->next->prior=s;
		s->prior=p;
		p->next=s;
		
		return true;
	}
	
}

bool ListDelete(DLinkList *&L,int i,ElemType &e)	//删除数据元素
{
	int j=0;
	DLinkList *p=L,*q;
	while (j<i-1 && p!=NULL)
	{
		j++;
		p=p->next;
	}
	if (p==NULL)				//未找到第i-1个结点
		return false;
	else						//找到第i-1个结点*p
	{
		q=p->next;				//q指向要删除的结点
		if (q==NULL) return false;	//不存在第i个结点
		e=q->data;
		p->next=q->next;		//从单链表中删除*q结点
		if (p->next!=NULL) p->next->prior=p;
		free(q);				//释放*q结点
		return true;
	}
}

void Sort(DLinkList *&head)	//双链表元素排序
{
	DLinkList *p=head->next,*q,*r;
	if (p!=NULL)			//若原双链表中有一个或以上的数据结点
	{
		r=p->next;			//r保存*p结点后继结点的指针
		p->next=NULL;		//构造只含一个数据结点的有序表
		p=r;
		while (p!=NULL)
		{
			r=p->next;		//r保存*p结点后继结点的指针
			q=head;
			while (q->next!=NULL && q->next->data<p->data)	//在有序表中找插入*p的前驱结点*q
				q=q->next;
			p->next=q->next;				//将*p插入到*q之后
			if (q->next!=NULL) q->next->prior=p;
			q->next=p;
			p->prior=q;
			p=r;
		}
	}
}

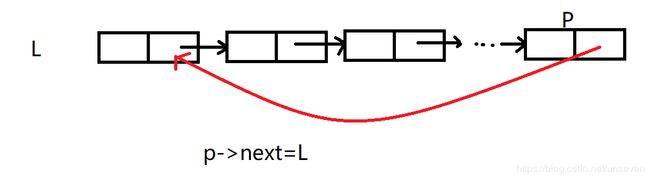
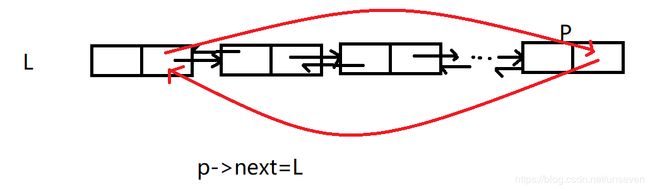
3.5循环链表

循环单链表：将表中尾结点的指针与改成指向表头结点，整个链表形成一个环。由此从表中任一结点出发，均可找到链表中其他结点。
循环双链表：形成两个环。