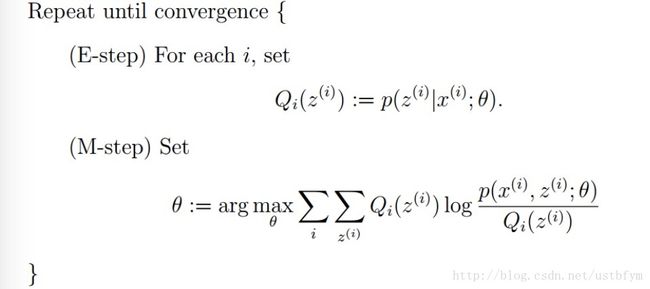EM推导PLSA模型

EM推导PLSA模型

回归EM算法

以上是EM算法的框架，基本思想是：

• E步骤：求当隐变量给定后当前估计的参数条件下的后验概率
• M步骤：最大化complete data对数似然函数的期望，把E步当做是已知值，得到新的参数值
• 不断迭代以上步骤直到收敛。

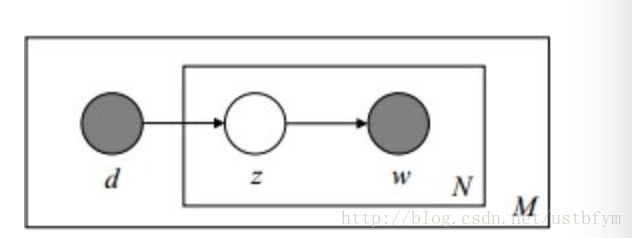
plsa模型简介

PLSA应用于信息检索、过滤、自然语言处理等领域，考虑到词分布和主题分布，可以看做概率化的矩阵分解，采用EM算法来学习参数。

模型示意图如下：

其中包括的概率有：

1. 以 p(di) p ( d i ) 的概率选中文档 di d i
2. 以 p(zk|di) p ( z k | d i ) 的概率选中主题 zk z k
3. 以 p(wj|zk) p ( w j | z k ) 的概率产生一个词 wj w j

在plsa中, p(di) p ( d i ) 可以事先计算求出， 而 p(wj|zk),p(zk|di) p ( w j | z k ) , p ( z k | d i ) 就是我们需要计算的参数。

根据EM算法：
E步： 求隐变量的后验概率

p(zk|di,wj)=p(wj|zk)p(zk|di)∑Kl=1p(wj|zl)p(zk|di) p ( z k | d i , w j ) = p ( w j | z k ) p ( z k | d i ) ∑ l = 1 K p ( w j | z l ) p ( z k | d i )

M步 完整数据的似然函数的期望

l=∑i∑jn(di,wj)logp(di,wj) l = ∑ i ∑ j n ( d i , w j ) l o g p ( d i , w j )
=∑i∑jn(di,wj)logp(wj|di)p(di) = ∑ i ∑ j n ( d i , w j ) l o g p ( w j | d i ) p ( d i )
=∑i∑jn(di,wj)logp(wj|di)+∑i∑jn(di,wj)logp(di) = ∑ i ∑ j n ( d i , w j ) l o g p ( w j | d i ) + ∑ i ∑ j n ( d i , w j ) l o g p ( d i )
后项是一个常数，因此可得
E(l)=∑i∑jn(di,wj)∑kp(zk|di,wj)log(p(wj,zk|di)) E ( l ) = ∑ i ∑ j n ( d i , w j ) ∑ k p ( z k | d i , w j ) l o g ( p ( w j , z k | d i ) )

=∑i∑jn(di,wj)∑kp(zk|di,wj)log(p(zk|di)p(wj|zk)) = ∑ i ∑ j n ( d i , w j ) ∑ k p ( z k | d i , w j ) l o g ( p ( z k | d i ) p ( w j | z k ) )

其中 n(di,wj) n ( d i , w j ) 表示 wj w j 在 di d i 中出现的次数， 同时因为概率隐藏着两个约束条件：
∑Mj=1p(wj|zk)=1 ∑ j = 1 M p ( w j | z k ) = 1
∑Kk=1p(zk|di)=1 ∑ k = 1 K p ( z k | d i ) = 1

由此可以看出，这是一个带等式约束的问题，可以采用拉格朗日乘子法来解决。

Lag=∑i∑jn(di,wj)∑kp(zk|di,wj)log(p(zk|di)p(wj|zk))+∑Kk=1τk(1−∑Mj=1p(wj|zk))+∑Ni=1ρi(1−∑Kk=1p(zk|di)) L a g = ∑ i ∑ j n ( d i , w j ) ∑ k p ( z k | d i , w j ) l o g ( p ( z k | d i ) p ( w j | z k ) ) + ∑ k = 1 K τ k ( 1 − ∑ j = 1 M p ( w j | z k ) ) + ∑ i = 1 N ρ i ( 1 − ∑ k = 1 K p ( z k | d i ) )

分别对带求解参数 p(wj|zk),p(zk|di) p ( w j | z k ) , p ( z k | d i ) 求偏导数可得
∂Lag∂p(wj|zk)=∑in(di,wj)p(zk|di,wj)p(wj|zk)−τk=0 ∂ L a g ∂ p ( w j | z k ) = ∑ i n ( d i , w j ) p ( z k | d i , w j ) p ( w j | z k ) − τ k = 0
∑in(di,wj)p(zk|di,wj)=τkp(wj|zk) ∑ i n ( d i , w j ) p ( z k | d i , w j ) = τ k p ( w j | z k )
∑Mm=1∑in(di,wj)p(zk|di,wj)=∑Mm=1τkp(wj|zk) ∑ m = 1 M ∑ i n ( d i , w j ) p ( z k | d i , w j ) = ∑ m = 1 M τ k p ( w j | z k )

∑Mm=1∑in(di,wj)p(zk|di,wj)=τk∑Mm=1p(wj|zk)=τk ∑ m = 1 M ∑ i n ( d i , w j ) p ( z k | d i , w j ) = τ k ∑ m = 1 M p ( w j | z k ) = τ k

将 τk τ k 代人可得

∑in(di,wj)p(zk|di,wj)=∑Mm=1∑in(di,wj)p(zk|di,wj)∗p(wj|zk) ∑ i n ( d i , w j ) p ( z k | d i , w j ) = ∑ m = 1 M ∑ i n ( d i , w j ) p ( z k | d i , w j ) ∗ p ( w j | z k )

p(wj|zk)=∑in(di,wj)p(zk|di,wj)∑Mm=1∑in(di,wj)p(zk|di,wj) p ( w j | z k ) = ∑ i n ( d i , w j ) p ( z k | d i , w j ) ∑ m = 1 M ∑ i n ( d i , w j ) p ( z k | d i , w j )

同理可得
∂Lag∂p(zk|di)=∑jn(di,wj)p(zk|di,wj)p(zk|di)−ρi=0 ∂ L a g ∂ p ( z k | d i ) = ∑ j n ( d i , w j ) p ( z k | d i , w j ) p ( z k | d i ) − ρ i = 0

∑jn(di,wj)p(zk|di,wj)=ρip(zk|di) ∑ j n ( d i , w j ) p ( z k | d i , w j ) = ρ i p ( z k | d i )
∑Kk=1∑jn(di,wj)p(zk|di,wj)=∑Kk=1ρip(zk|di) ∑ k = 1 K ∑ j n ( d i , w j ) p ( z k | d i , w j ) = ∑ k = 1 K ρ i p ( z k | d i )
∑Kk=1∑jn(di,wj)p(zk|di,wj)=ρi∑Kk=1p(zk|di)=ρi ∑ k = 1 K ∑ j n ( d i , w j ) p ( z k | d i , w j ) = ρ i ∑ k = 1 K p ( z k | d i ) = ρ i

将 ρi ρ i 代入
∑jn(di,wj)p(zk|di,wj)=∑Kk=1∑jn(di,wj)p(zk|di,wj)∗p(zk|di) ∑ j n ( d i , w j ) p ( z k | d i , w j ) = ∑ k = 1 K ∑ j n ( d i , w j ) p ( z k | d i , w j ) ∗ p ( z k | d i )

可得
p(zk|di)=∑jn(di,wj)p(zk|di,wj)∑Kk=1∑jn(di,wj)p(zk|di,wj) p ( z k | d i ) = ∑ j n ( d i , w j ) p ( z k | d i , w j ) ∑ k = 1 K ∑ j n ( d i , w j ) p ( z k | d i , w j )

M步更新这两个参数