matlab遗传算法(GA)详解(一)算法入门
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解(所找到的解是全局最优解)的方法。
参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
1)种群初始化。我们需要首先通过随机生成的方式来创造一个种群,一般该种群的数量为100~500,这里我们采用二进制将一个染色体(解)编码为基因型。随后用进制转化,将二进制的基因型转化成十进制的表现型。
2)适应度计算(种群评估)。这里我们直接将目标函数值作为个体的适应度。
3)选择(复制)操作。根据种群中个体的适应度大小,通过轮盘赌等方式将适应度高的个体从当前种群中选择出来。其中轮盘赌即是与适应度成正比的概率来确定各个个体遗传到下一代群体中的数量。
具体步骤如下:
(1)首先计算出所有个体的适应度总和Σfi。
(2)其次计算出每个个体的相对适应度大小fi/Σfi,类似于softmax。
(3)再产生一个0到1之间的随机数,依据随机数出现在上述哪个概率区域内来确定各个个体被选中的次数。
4)交叉(交配)运算。该步骤是遗传算法中产生新的个体的主要操作过程,它用一定的交配概率阈值(pc,一般是0.4到0.99)来控制是否采取单点交叉,多点交叉等方式生成新的交叉个体。
具体步骤如下:
(1)先对群体随机配对。
(2)再随机设定交叉点的位置。
(3)再互换配对染色体间的部分基因。
5)变异运算。该步骤是产生新的个体的另一种操作。一般先随机产生变异点,再根据变异概率阈值(pm,一般是0.0001到0.1)将变异点的原有基因取反。
6)终止判断。如果满足条件(迭代次数,一般是200~500)则终止算法,否则返回step2。
![]()
我们首先从函数出发,既然是寻找全局最优解,我们可以想象一个多元函数的图像。遗传算法中每一条染色体,对应着遗传算法的一个解决方案,一般我们用适应性函数(fitness function)来衡量这个解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。可以把遗传算法的过程看作是一个在多元函数里面求最优解的过程。可以这样想象,这个多维曲面里面有数不清的“山峰”,而这些山峰所对应的就是局部最优解。而其中也会有一个“山峰”的海拔最高的,那么这个就是全局最优解。而遗传算法的任务就是尽量爬到最高峰,而不是陷落在一些小山峰。(另外,值得注意的是遗传算法不一定要找“最高的山峰”,如果问题的适应度评价越小越好的话,那么全局最优解就是函数的最小值,对应的,遗传算法所要找的就是“最深的谷底”)
![]()
我们从一元函数出发,已知这样一个函数:
![]()
在matlab下绘制该函数图像 我们可以发现
x=-1:0.01:2; %从-1到2 每隔0.01取一个点绘制图像
y = x.*sin(10*pi*x) + 2;
plot(x,y)我们可以发现
我们尝试寻找这个函数在定义域内的最高点和最低点,可以尝试下列几种方法:
既然我们把函数曲线理解成一个一个山峰和山谷组成的山脉。那么我们可以设想所得到的每一个解就是一只袋鼠,我们希望它们不断的向着更高处跳去,直到跳到最高的山峰。所以求最大值的过程就转化成一个“袋鼠跳”的过程。
下面介绍介绍“袋鼠跳”的几种方式。
爬山算法:一只袋鼠朝着比现在高的地方跳去。它找到了不远处的最高的山峰。但是这座山不一定是最高峰。这就是爬山算法,它不能保证局部最优值就是全局最优值。
模拟退火:袋鼠喝醉了。它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高峰跳去。这就是模拟退火算法。
遗传算法:有很多袋鼠,它们降落到喜玛拉雅山脉的任意地方。这些袋鼠并不知道它们的任务是寻找珠穆朗玛峰。但每过几年,就在一些海拔高度较低的地方射杀一些袋鼠。于是,不断有袋鼠死于海拔较低的地方,而越是在海拔高的袋鼠越是能活得更久,也越有机会生儿育女。就这样经过许多年,这些袋鼠们竟然都不自觉地聚拢到了一个个的山峰上,可是在所有的袋鼠中,只有聚拢到珠穆朗玛峰的袋鼠被带回了美丽的澳洲。
而这里我们使用的就是遗传算法来解决这个问题,首先我们使用matlab中的ga()函数来直接寻找到答案。
关于ga函数就是将上面的算法思想进行封装成的一个函数
首先创建一个函数 一个脚本
在函数中我们定义目标函数
function y = simple_fitness(x)
y = x*sin(10*pi*x)+2
end
在函数中我们使用ga算法求解
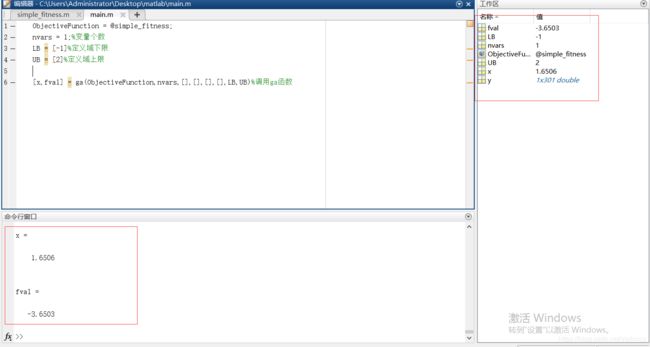
ObjectiveFunction = @simple_fitness;
nvars = 1;%变量个数
LB = [-1]%定义域下限
UB = [2]%定义域上限
[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],LB,UB)%调用ga函数这里要注意ga算法默认的全局最优解是全局的最小值 我们这里先求出最小值
本次遗传算法得出在1.9505有最小值0.0497
但是这个只是预测值 与真实值不同 每次遗传迭代的结果也是不同的 下次迭代结果有可能不是这个数值
Matlab工具箱函数 ga 是求最小值,所有优化工具箱函数都是求最小值,你如果要求最大值,把目标函数取负,然后求得最小值实际上就是原始目标函数的最大值了。这也是为什么matlab里所有优化工具箱函数都是求最小值了
修改目标函数为
function y = simple_fitness(x)
y = -x*sin(10*pi*x)-2
end得到最大值是在1.6506处取得的3.6503