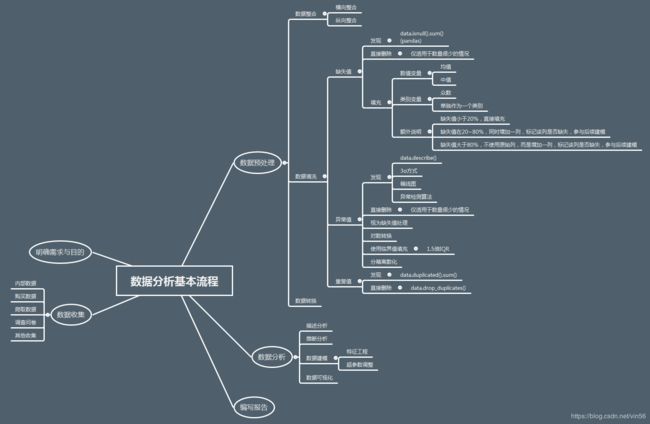
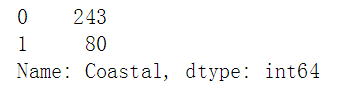项目实例：使用python及相关库实现AQI分析与预测

前言

一、项目背景

AQI(Air Quality Index)，即空气质量指数，用来衡量空气清洁或污染的程度。值越小，表示空气质量越好。近年来因为环境问题，空气质量也越来越受到人们重视。
分析旨在通过采集到的国内各城市数据，运用数据分析相关技术，对全国城市空气质量进行研究与分析。

二、提出问题

• 空气质量较好/较差的城市是哪些？
• 空气质量在地理位置分布上是否具有一定规律性？
• 临海城市的空气质量是否有别于内陆城市？
• 空气质量主要受哪些因素影响？
• 全国城市空气质量普遍处于何种水平？
• 怎样预测一个城市的空气质量？

三、数据预览

数据为2015年空气质量质数集，包含国内主要城市的相关数据以及空气质量指数。

列名	含义
City	城市名
AQI	空气质量指数
Precipitation	降雨量
GDP	城市生产总值
Temperature	温度
Longitude	经度
Latitude	维度
Altitude	海拔高度
PopulationDensity	人口密度
Coastal	是否沿海
GreenCoverageRate	绿化覆盖率
Incineration(10,000ton)	焚烧量（万吨）

四、数据清洗

# 导入相关库，进行初始化设置
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings

sns.set(style="darkgrid")
plt.rcParams["font.family"] = "SimHei" # 设置字体样式
plt.rcParams["axes.unicode_minus"] = False # 设置正常显示坐标轴负号
warnings.filterwarnings("ignore") # 忽略警告消息

# 一、读取数据预览
data = pd.read_csv("data.csv")
data.head()

# 二、数据处理
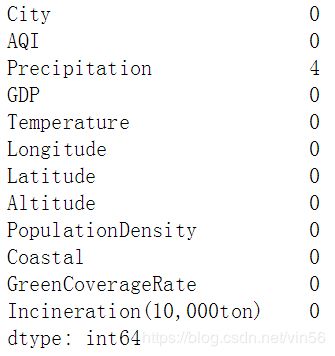
# 1、首先查看缺失值情况
print(data.isnull().sum())

# 对于数值类型使用均值或者中位数填充。
# 查看Precipitation列分布偏度
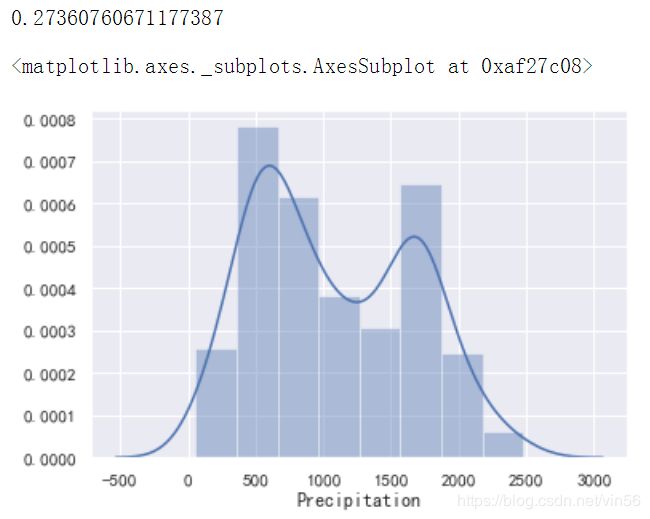
print(data["Precipitation"].skew())
sns.distplot(data["Precipitation"].dropna()) # 函数画图需要去掉空值

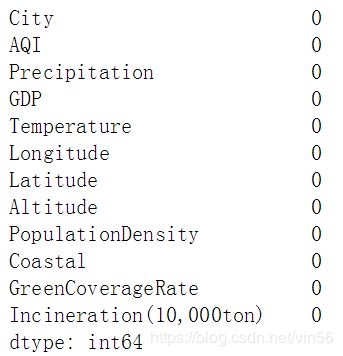
# 稍微右偏，使用中位数填充，查看填充后的缺失值情况
data["Precipitation"].fillna(data["Precipitation"].median(), inplace=True)
print(data.isnull().sum())

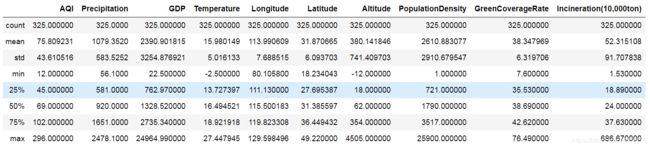
# 2、处理异常值，先查看大致的统计信息
data.describe()

# 可以看到GDP上三分位和最大值差距巨大，可能存在异常值（其他特征待后续建立模型时处理）
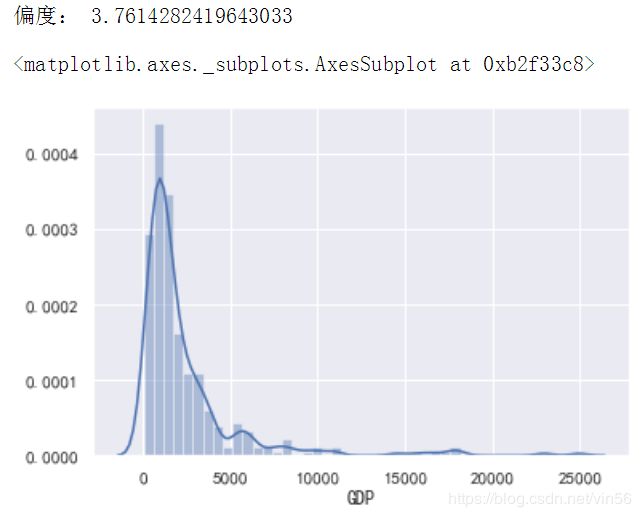
# 查看GDP数据的偏度
print("偏度：", data["GDP"].skew())
sns.distplot(data["GDP"])

# 可以看出GDP列严重右偏，需要进行正态化
# 根据正态分布特性，对于3σ之外的数据视为异常值
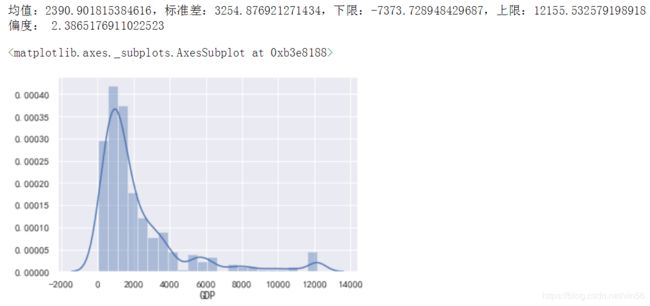
mean, std = data["GDP"].mean(), data["GDP"].std()
lower, upper = mean - 3 * std, mean + 3 * std
print("均值：%s，标准差：%s，下限：%s，上限：%s" % (mean, std, lower, upper))

# 将异常值替换为边界值
data["GDP"][data["GDP"]<lower] = lower
data["GDP"][data["GDP"]>upper] = upper

# 查看处理后的结果
print("偏度：",data["GDP"].skew())
sns.distplot(data["GDP"])

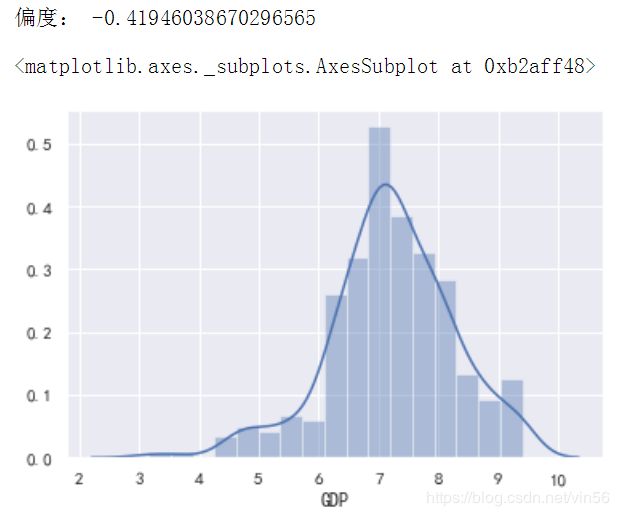
# 效果不是很明显，直接取对数来处理

# 定义函数取对数
def getLog(x):
    # 对数只能处理真数为正数的值，所以需要单独拿到符号再乘以绝对值的对数
    return np.sign(x) * np.log(np.abs(x)+1)

data["GDP"] = pd.DataFrame(data=data["GDP"].apply(getLog), index=data["City"].index)

# 查看处理后的偏度和分布情况
print("偏度：", data["GDP"].skew())
sns.distplot(data["GDP"])

# 对于重复值，直接删除即可
data.drop_duplicates(inplace=True)
print(data.duplicated().sum()) # 0

五、数据分析

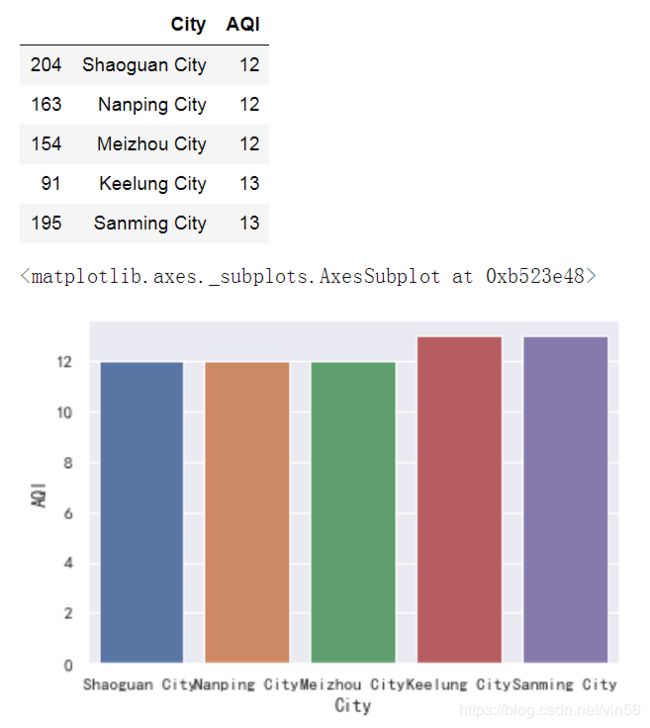
# 空气质量最好的五个城市
t = data[["City","AQI"]].sort_values("AQI")
display(t.iloc[:5])
sns.barplot(x="City", y="AQI", data=t.iloc[:5])

# 空气质量最差的五个城市
display(t.iloc[-5:])
sns.barplot(x="City", y="AQI", data=t.iloc[-5:])

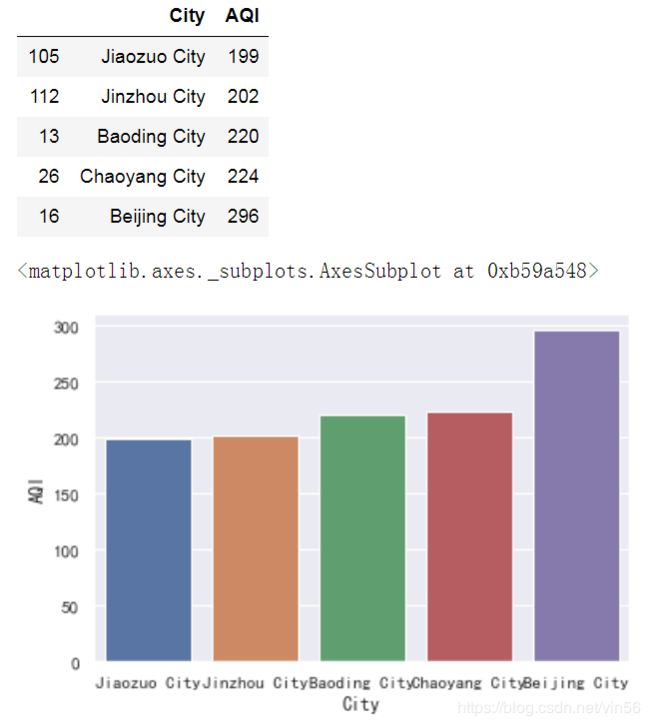
1、根据以上可以得出结论：
空气最好的五个城市为：韶关、南平、梅州、基隆、三明
空气最差的五个城市为：北京、朝阳、保定、锦州、焦作

# 根据数据绘制城市空气质量分布图
sns.scatterplot(x="Longitude", y="Latitude", hue="AQI", palette=plt.cm.RdYlGn_r, data=data)

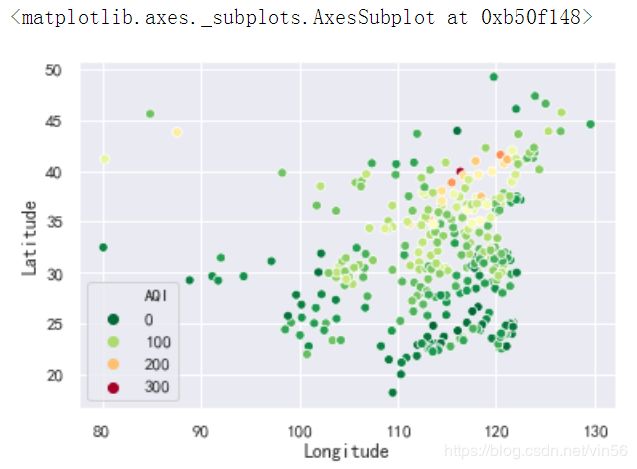
2、从以上可以发现，从大致的地理位置上看，西部城市优于东部城市，南部城市优于北部城市。

# 临海城市空气质量是否优于内陆城市

# 首先查看对应数据数量
display(data["Coastal"].value_counts())
sns.countplot(x="Coastal", data=data)

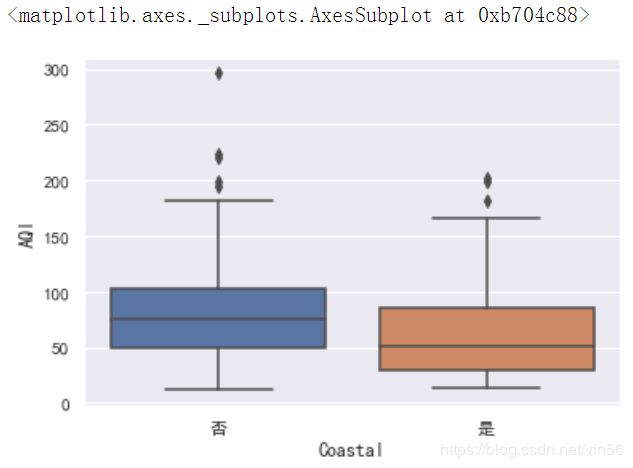
# 查看不同类别箱线图
sns.boxplot(x="Coastal", y="AQI", data=data)

从样本数据箱线图看，临海城市空气质量大致优于内陆城市。

# 接下来根据样本数据，推断总体参数的对比
# 此时总体均值未知，样本容量较大，选择进行两个样本的t检验
from scipy import stats

coastal = data[data["Coastal"]=="是"]["AQI"]
inland = data[data["Coastal"]=="否"]["AQI"]

# 首先进行方差齐性检验，是两个独立样本进行t检验的基础。这里假设临海与内陆AQI总体方差一致。
stats.levene(coastal, inland)

# pvalue=0.77 > 0.05，即有95%置信度认为两个样本总体方差一致
# 进行两个样本t检验（方差是否一致会影响检验结果，equal_var参数根据方差一致性传入）
r = stats.ttest_ind(coastal, inland, equal_var=True)
print(r)

# 假设临海城市空气质量优于内陆城市，计算p值
p = stats.t.sf(r.statistic, df=len(coastal)+len(inland)-2)
print(p)

3、根据以上可得结论：有超过99%的几率维持原假设，即认为临海城市的空气质量普遍好于内陆城市。

# 空气质量主要受哪些因素影响？
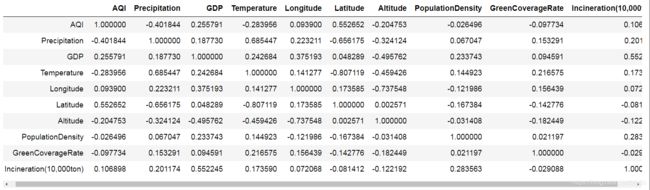
# 首先查看各因素之间的相关系数
data.corr()

# 使用热图展示相关系数结果
plt.figure(figsize=(16, 10))
ax = sns.heatmap(data.corr(), cmap=plt.cm.RdYlGn, annot=True, fmt=".2f")
# Matplotlib版本问题导致首尾行显示不全，调整边界
a, b = ax.get_ylim()
ax.set_ylim(a+0.5, b-0.5)

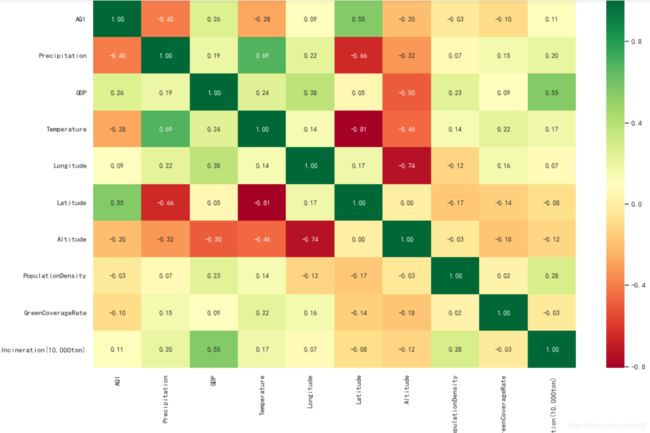
4、根据以上可以得出结论：
空气质量指数主要受降雨量（0.40）与维度（0.55）影响。

• 降雨量越多，空气质量越好。
• 维度越低，空气质量越好。

# 传闻全国所有城市的空气质量指数均值在71左右，验证消息是否可靠。

# 样本城市平均空气质量指数
data["AQI"].mean() # 75.3343653250774

# 根据样本数据推断假设的总体均值，假设全国所有城市的空气质量指数均值为71
# 总体方差未知，样本量较大认为满足正态分布，使用t检验，置信度为95%
r = stats.ttest_1samp(data["AQI"], 71)
print("t值：", r.statistic)
print("p值：", r.pvalue)

# p=0.07 > 0.05，无法拒绝原假设，即维持原假设全国所有城市空气质量指数均值在71左右

# 获得置信区间
mean = data["AQI"].mean()
std = data["AQI"].std()
stats.t.interval(0.95, df=len(data)-1, loc=mean, scale=std/np.sqrt(len(data)))

5、根据以上可以得出结论：
在95%的置信度下，认为全国所有城市空气质量指数均值在70.63~80.04之间

# 建立模型，实现通过部分指标预测空气质量指数
# 处理所有特征异常值
# 首先将非数值数据转换为数值类型
data["Coastal"] = data["Coastal"].map({"是":1, "否":0})
data["Coastal"].value_counts()

# 不进行任何处理，先建立基模型，后续在该模型上进行改进

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

X = data.drop(["City","AQI"], axis=1) # 城市名不用作为预测系数，AQI作为预测值充当y值
y = data["AQI"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)
print("训练集r2: ", lr.score(X_train, y_train))
print("测试集r2: ", lr.score(X_test, y_test))

# 处理每个连续变量特征的异常值，通过是否超过1.5倍IQR判断是否异常
for col in X.columns.drop("Coastal"):
    quantile = np.quantile(X_train[col], [0.25, 0.75])
    IQR = quantile[1] - quantile[0]
    lower = quantile[0] - 1.5 * IQR
    upper = quantile[1] + 1.5 * IQR
    X_train[col][X_train[col]<lower] = lower
    X_train[col][X_train[col]>upper] = upper
    X_test[col][X_test[col]<lower] = lower
    X_test[col][X_test[col]>upper] = upper

# 效果对比
lr.fit(X_train, y_train)
print("训练集r2：", lr.score(X_train, y_train))
print("测试集r2：", lr.score(X_test, y_test))

效果稍微有点提高，下面使用特征选择剔除部分特征

# 特征选择，使用RFECV，递归特征消除交叉验证
from sklearn.feature_selection import RFECV
rfecv = RFECV(estimator=lr, step=1, cv=5, n_jobs=-1, scoring="r2")
rfecv.fit(X_train, y_train)
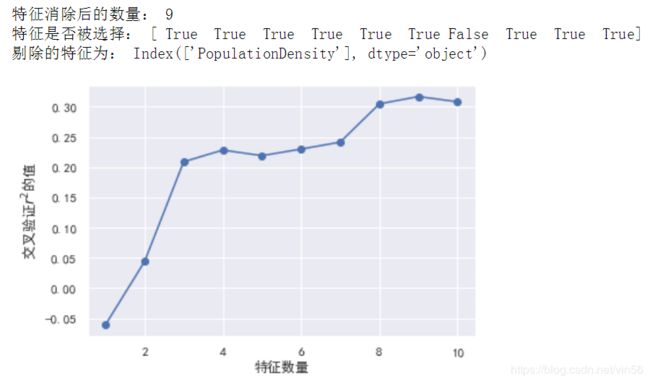
print("特征消除后的数量：", rfecv.n_features_)
print("特征是否被选择：", rfecv.support_)
# 查看不同数量特征时的交叉验证结果
plt.plot(range(1,len(rfecv.grid_scores_)+1), rfecv.grid_scores_, marker="o")
plt.xlabel("特征数量")
plt.ylabel("交叉验证$r^2$的值")
print("剔除的特征为：", X_train.columns[~rfecv.support_])

# 使用特征选择后的数据跑模型
X_train_eli = X_train[X_train.columns[rfecv.support_]]
X_test_eli = X_test[X_test.columns[rfecv.support_]]
print("训练集r2：", rfecv.estimator_.score(X_train_eli, y_train))
print("测试集r2：", rfecv.estimator_.score(X_test_eli, y_test))

可以看出剔除特征后的r2基本没有差别，说明剔除的特征对拟合目标没有帮助，可以去掉。
接下来对特征进行分箱离散化。

# 对可能非线性关系的特征进行分箱离散化

from sklearn.preprocessing import KBinsDiscretizer
k = KBinsDiscretizer(n_bins=[4, 5, 14, 6], encode="onehot-dense", strategy="uniform")
discretize = ["Longitude", "Temperature", "Precipitation", "Latitude"] # 定义离散化特征

# 获得离散化特征之外的其他特征并合并
r = k.fit_transform(X_train_eli[discretize]) # 返回一个ndarry数组
r = pd.DataFrame(r, index=X_train_eli.index)
X_train_dis = X_train_eli.drop(discretize, axis=1)
X_train_dis = pd.concat([X_train_dis, r], axis=1)

# 对测试集进行同样操作，测试集不用训练直接转换
r = pd.DataFrame(k.transform(X_test_eli[discretize]), index=X_test_eli.index)
X_test_dis = X_test_eli.drop(discretize, axis=1)
X_test_dis = pd.concat([X_test_dis, r], axis=1)

X_train_dis.head()

# 对离散后的数据进行训练
lr.fit(X_train_dis, y_train)
print("训练集r2：", lr.score(X_train_dis, y_train))
print("测试集r2：", lr.score(X_test_dis, y_test))

可以看出拟合结果有了进一步提升。
继续查看残差图，调整模型异方差性。

# 观察残差图
model = LinearRegression()
model.fit(X_train_dis, y_train)
y_hat_train = model.predict(X_train_dis)
residual = y_hat_train - y_train.values
sns.scatterplot(x=y_hat_train, y=residual)
plt.xlabel("预测值")
plt.ylabel("残差")
plt.title("预测值残差分布")
plt.axhline(y=0, color="r")

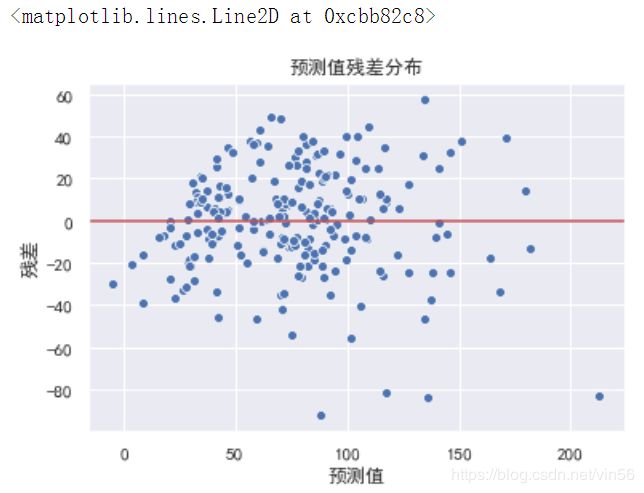
根据残差图看出，随着预测值增大，模型误差也在增大，可以使用对目标y值取对数进行处理

model = LinearRegression()
y_train_log = np.log(y_train)
y_test_log = np.log(y_test)
# 使用处理后的y值进行拟合
model.fit(X_train, y_train_log)

y_hat_train = model.predict(X_train)
residual = y_hat_train - y_train_log.values
sns.scatterplot(x=y_hat_train, y=residual)
plt.xlabel("预测值")
plt.ylabel("残差")
plt.title("预测值残差分布")
plt.axhline(y=0, color="r")

此时，异方差性得到解决，模型的效果可能会得到一定的提升。

# 根据残差图，检测离群点
y_hat_train = lr.predict(X_train_dis)
residual = y_hat_train - y_train.values

r = (residual-residual.mean()) / residual.std() # 标准化残差

plt.xlabel("预测值")
plt.ylabel("残差")
plt.axhline(y=0, color="r")

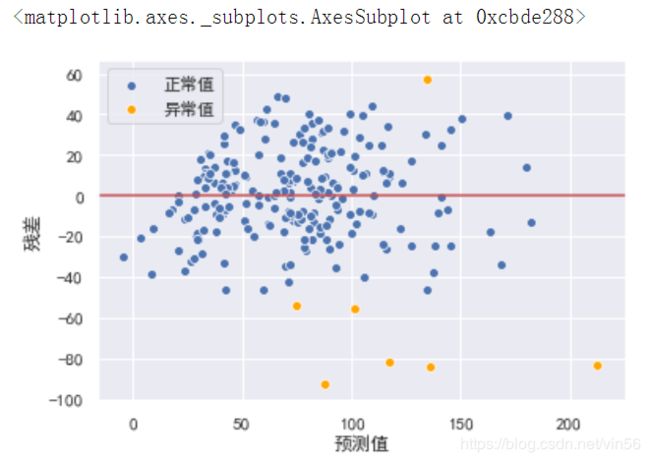
# 有95%置信度认为标准化残差落在(-2,2)区间内的为正常值，否则为异常值
sns.scatterplot(x=y_hat_train[np.abs(r)<=2], y=residual[np.abs(r)<2], color="b", label="正常值")
sns.scatterplot(x=y_hat_train[np.abs(r)>2], y=residual[np.abs(r)>=2], color="orange", label="异常值")

# 根据残差去除异常值并进行拟合
X_train_dis_filter = X_train_dis[np.abs(r)<=2]
y_train_filter = y_train[np.abs(r)<=2]
lr.fit(X_train_dis_filter, y_train_filter)
print("训练集r2：", lr.score(X_train_dis_filter, y_train_filter))
print("测试集r2：", lr.score(X_test_dis, y_test))

6、至此，模型建立结束。通过模型，可以根据特征数据预测一个城市的空气质量指数。

六、总结

1、空气质量从总体分布上来说，南部城市优于北部城市，西部城市优于东部城市。
2、临海城市的空气质量整体上优于内陆城市。
3、是否临海、降雨量与维度对空气质量指数的影响较大。
4、我国城市平均空气质量指数大致在(70.63 ~ 80.04)这个区间内，置信度为95%。
5、通过历史数据，我们可以对空气质量指数进行预测。

（PS: 数据可视化与报告待定。数据如有问题欢迎指出。）