运筹学中的节约里程法及其python实现

节约里程法简介

节约里程法，又称C-W算法 、节约算法或节约法，是由Clarke和Wright于1964年首次提出的，用来解决VRP问题，是重要的物流算法，是用来解决运输车辆数目不确定的问题的最有名的启发式算法。

节约里程法核心思想是依次将运输问题中的两个回路合并为一个回路，每次使合并后的总运输距离减小的幅度最大，直到达到一辆车的装载限制时，再进行下一辆车的优化。优化过程分为并行方式和串行方式两种。

利用节约法确定配送路线的主要出发点是，根据配送中心的运输能力和配送中心到各个用户以及各个用户之间的距离来制定使总的车辆运输的吨公里数最小的配送方案。另还需满足以下条件；（1）所有用户的要求；（2）不使任何一辆车超载；（3）每辆车每天的总运行时间或行驶里程不超过规定的上限；（4）用户到货时间要求。

基本原理

基本思想为为达到高效率的配送，使配送的时间最小距离最短成本最低，而寻找的最佳配送路线。

假定有n个访问地，把每个访问地看成一个点，并取其中的一个点为基点（起点），例如以1点为基点。首先将每个点与该基点相连接，构成线路1→j→1（j=2,3,…,n），这样就得到了一个具有n-1条线路的图（当然，这时尚未形成Hamilton回路）。旅行者按此线路访问这n个点所走的路程总和为
$$z=\sum _{j=2}^n{C}_{1j}$$
其中$C_{1j}$为由点1到点j的路段长度，注意此处假定$C_{1j}=C_{j1}$（对所有j）。

若连接点i和点j，即使旅行者走弧（i,j）时（当然这时就不再经过弧（i,1）和弧（1，j），所引起的路程节约值s(i,j)可计算如下
$$s(i,j)=2c_{1i}+2c_{1j}-c_{1i}+c_{1j}+c_{ij})=c_{1i}+c_{1j}-c_{ij}$$
对不同的点对(i,j)，s(i,j)越大，旅行者通过弧(i,j)时所节约的路程越多，因而应优先将其安排到旅行线路中去，使旅行者旅行时通过这一条弧。

迭代步骤

在具体应用该方法时，可按以下步骤进行。

（1）选取基点，例如以1点为基点。将每个点与该基点相连接，得到n-1条线路1→j→1（j=2,3,…,n）。
（2）对不违背限制条件的所有可连接点对(i,j)，如下计算其节约值（i,j不为基点）
$$s(i,j)==c_{1i}+c_{1j}-c_{ij}$$
（3）将所有$s(i,j)$按其值的大小由大到小排列。
（4）按$s(i,j)$的上述顺序，逐个考察其端点i和j，若满足以下条件，就将弧（i,j）插入到线路中。其条件是：
a. 点i和点j不在一条线路上；
b. 点i和点j均与基点相邻。
（5）返回步骤（4），直至考察完所有可插入弧（i,j）为止。
通过以上各迭代步骤，使问题的解逐步得到改善，最后达到满意解（也有可能达到最优解）。

例题

已知配送中心P0向5个用户Pj配送货物，其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图所示，配送中心有3台2t卡车和2台4t两种车辆可供使用。利用节约里程法制定最优的配送方案。

第一步，作运输里程表，列出配送中心到用户及用户间的最短距离。

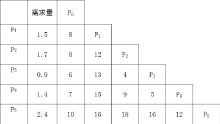
第二步，按节约里程公式求得相应的节约里程数。

第三步，将节约里程按从大到小顺序排列。

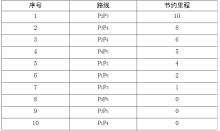
第四步，根据载重量约束与节约里程大小，顺序连接各客户结点，形成两个配送线。
P2P3－P3P4－P2P4－P4P5－P1P2－P1P5－P1P3－P2P5－P3P5－P1P4

得出结果：
配送线路一：
运量=1.7+0.9+1.4=4t
运行距离=8+4+5+7=24km
用一辆4t车运送，节约距离为18km
配送线路二：
运量=2.4+1.5=3.9t<4t
运行距离=8+10+16=34km
用一辆4t车运送，节约距离为2km

初始方案：配送线路5条，需要车5辆，配送距离=39*2=78km
优化后的方案：2条配送路线,2辆4t车，配送距离=24+34=58km

python程序

import csv
from operator import itemgetter

class Vrp():

    # -----------初始数据定义---------------------

    def __init__(self):
        self.mans = 9                                                   # 客户数量
        self.tons = 3                                                   # 车辆载重
        self.distanceLimit = 1000                                       # 车辆一次行驶的最大距离
        self.distance = []                                              # 各个客户及配送中心距离
        self.q = [0, 1, 1.1, 0.9, 0.8, 1.1, 0.4, 0.7, 0.8, 0.9]         # 10个客户分布需要的货物的需求量，第0位为配送中心自己
        self.savings = []                                               # 节约度
        self.Routes = []                                                # 路线
        self.Cost = 0                                                   # 总路程

    # -----------导入距离数据---------------------

    def datainput(self):
        with open("data.csv", "r") as csvfile:
            reader = csv.reader(csvfile)
            for line in reader:
                line = [float(x) for x in line]
                self.distance.append(line)

    # -----------节约算法主程序---------------------

    def savingsAlgorithms(self):
        saving = 0
        for i in range(1, len(self.q)):
            self.Routes.append([i])

        for i in range(1, len(self.Routes) + 1):                                                 # 使用Sij = Ci0 + C0j - Cij计算节约度
            for j in range(1, len(self.Routes) + 1):
                if i == j:
                    pass
                else:
                    saving = (self.distance[i][0] + self.distance[0][j]) - self.distance[i][j]
                    self.savings.append([i, j, saving])                                          # 将结果以元组形式存放在列表中

        self.savings = sorted(self.savings, key=itemgetter(2), reverse=True)                     # 按照节约度从大到小进行排序
        for i in range(len(self.savings)):
            print(self.savings[i][0],'--',self.savings[i][1], "  ",self.savings[i][2])           # 打印节约度

        for i in range(len(self.savings)):
            startRoute = []
            endRoute = []
            routeDemand = 0
            for j in range(len(self.Routes)):
                if (self.savings[i][0] == self.Routes[j][-1]):
                    endRoute = self.Routes[j]
                elif (self.savings[i][1] == self.Routes[j][0]):
                    startRoute = self.Routes[j]

                if ((len(startRoute) != 0) and (len(endRoute) != 0)):
                    for k in range(len(startRoute)):
                        routeDemand += self.q[startRoute[k]]
                    for k in range(len(endRoute)):
                        routeDemand += self.q[endRoute[k]]
                    routeDistance = 0
                    routestore = [0]+endRoute+startRoute+[0]
                    for i in range(len(routestore)-1):
                        # print(routestore[i],routestore[i+1])
                        # print(self.distance[routestore[i]][routestore[i+1]])
                        routeDistance += self.distance[routestore[i]][routestore[i+1]]

                    #print(routestore,"== ==:",routeDistance)

                    if (routeDemand <= self.tons) and (routeDistance <= self.distanceLimit):     # 按照限制规则对​​路线进行更改
                        self.Routes.remove(startRoute)
                        self.Routes.remove(endRoute)
                        self.Routes.append(endRoute + startRoute)
                    break

        for i in range(len(self.Routes)):
            self.Routes[i].insert(0, 0)
            self.Routes[i].insert(len(self.Routes[i]), 0)

    # -----------输出最终结果---------------------

    def printRoutes(self):
        for i in self.Routes:
            costs = 0
            for j in range(len(i)-1):
                costs += self.distance[i[j]][i[j+1]]
            print("路线:  ",i,"  路程:  ",costs)

    def calcCosts(self):
        for i in range(len(self.Routes)):
            for j in range(len(self.Routes[i]) - 1):
                self.Cost += self.distance[self.Routes[i][j]][self.Routes[i][j + 1]]

        print("\nTotal Distance: ", round(self.Cost, 3))

    # -----------Master函数---------------------

    def start(self):                      # Master函数，调用所有其他函数
        print("== == == == == == == == == == == == == == == 导入数据 == == == == == == == = == == == == == == == =")
        self.datainput()
        print("== == == 距离表 == == ==")
        for i in self.distance:
            print(i)
        print("== == == 需求表 == == ==")
        print(self.q)
        print("== == == 限制条件 == == ==")
        print("车辆最大载重：",self.tons)
        print("车辆最长运输距离：", self.distanceLimit)
        print("== == == == == == == == == == == == == == == 节约度 == == == == == == == = == == == == == == == =")
        self.savingsAlgorithms()          # 函数调用计算节省量并生成路线
        print("== == == == == == == == == == == == == == == 结果 == == == == == == == = == == == == == == == =")
        self.printRoutes()
        self.calcCosts()
        self.datainput()


if __name__ == '__main__':
	vrp = Vrp()
	vrp.start()

参考网址：
节约里程法-百度百科
节约里程算法的python实现（含github地址）
C# 节约里程法实现（原理很详细，还有例题）