用python3实现差分进化算法（DE）

【注】：完整源码在我的github上，找不找得到就看自己咯 ^ _ ^

差分进化算法(Differential Evolution Algorithm，DE)是一种高效的全局优化算法。它也是基于群体的启发式搜索算法，群中的每个个体对应一个解向量。差分进化算法的进化流程则与遗传算法非常类似，都包括变异、杂交和选择操作，但这些操作的具体定义与遗传算法有所不同。
差分算法的具体流程如下(以下各式都是针对某一维来说的)：

1.初始化

一般通过以下式子来进行初始化：

$x_i=x_{min}+rand\ast (x_{max}-x_{min})$

其中，$x_{min}$、$x_{max}$是其某一维的取值边界，$rand$为（0,1）之间的随机数

2.变异

父代个体间选择两个个体进行向量做差生成差分矢量，然后，选择另外一个个体与差分矢量求和生成实验个体。表达式如下：

$v_i=x_{r1}+F\ast (x_{r2}-x_{r3})$

其中，$r1$,$r1$,$r1$为3个不相等的随机数，并且和$i$不等。$F$为缩放因子，一般在[0,2]之间选择，通常取0.5，$F$主要影响算法的全局寻优能力。$F$越小，算法对局部的搜索能力更好，$F$越大算法越能跳出局部极小点，但是收敛速度会变慢。

3.交叉

分两种情况：
1.如果$rand<=CR$ 或者$j=j_{rand}$：$u_i=v_i$
2.不满足1的条件时：$u_i=x_i$

其中，$CR$为交叉概率，取值范围为[0,1]之间的随机浮点数。$j_{rand}$为[0，NP]间的随机整数，NP为种群大小。$CR$主要反映的是在交叉的过程中，子代与父代、中间变异体之间交换信息量的大小程度。$CR$的值越大，信息量交换的程度越大。

4.选择

DE采用贪婪选择的策略，选择较优的个体作为新的个体，也分2种情况。选择的过程如下：
1.如果$f(u_i)<f(x_i)$，则$x_{i+1}=u_i$
2.如果不满足1的条件，则$x_{i+1}=x_i$
其中，$f()$代表适应函数。

可以结合一下流程图来了解：

下面上主要代码：

import numpy as np
import random

class DE:
    def __init__(self, dim, size, iter_num, x_min, x_max, best_fitness_value=float('Inf'), F = 0.5, CR = 0.8):
        self.F = F
        self.CR = CR
        self.dim = dim  # 维度
        self.size = size  # 总群个数
        self.iter_num = iter_num  # 迭代次数
        self.x_min = x_min
        self.x_max = x_max
        self.best_fitness_value = best_fitness_value
        self.best_position = [0.0 for i in range(dim)]  # 全局最优解
        self.fitness_val_list = []  # 每次迭代最优适应值

        # 对种群进行初始化
        self.unit_list = [Unit(self.x_min, self.x_max, self.dim) for i in range(self.size)]


    # 变异
    def mutation_fun(self):
        for i in range(self.size):
            r1 = r2 = r3 = 0
            while r1 == i or r2 == i or r3 == i or r2 == r1 or r3 == r1 or r3 == r2:
                r1 = random.randint(0, self.size - 1)  # 随机数范围为[0,size-1]的整数
                r2 = random.randint(0, self.size - 1)
                r3 = random.randint(0, self.size - 1)
            mutation = self.get_kth_unit(r1).get_pos() + \
                       self.F * (self.get_kth_unit(r2).get_pos() - self.get_kth_unit(r3).get_pos())
            for j in range(self.dim):
                #  判断变异后的值是否满足边界条件，不满足需重新生成
                if self.x_min <= mutation[j] <= self.x_max:
                    self.get_kth_unit(i).set_mutation(j, mutation[j])
                else:
                    rand_value = self.x_min + random.random()*(self.x_max - self.x_min)
                    self.get_kth_unit(i).set_mutation(j, rand_value)

    # 交叉
    def crossover(self):
        for unit in self.unit_list:
            for j in range(self.dim):
                rand_j = random.randint(0, self.dim - 1)
                rand_float = random.random()
                if rand_float <= self.CR or rand_j == j:
                    unit.set_crossover(j, unit.get_mutation()[j])
                else:
                    unit.set_crossover(j, unit.get_pos()[j])

    # 选择
    def selection(self):
        for unit in self.unit_list:
            new_fitness_value = fit_fun(unit.get_crossover())
            if new_fitness_value < unit.get_fitness_value():
                unit.set_fitness_value(new_fitness_value)
                for i in range(self.dim):
                    unit.set_pos(i, unit.get_crossover()[i])
            if new_fitness_value < self.get_bestFitnessValue():
                self.set_bestFitnessValue(new_fitness_value)
                for j in range(self.dim):
                    self.set_bestPosition(j, unit.get_crossover()[j])

    def update(self):
        for i in range(self.iter_num):
            self.mutation_fun()
            self.crossover()
            self.selection()
            self.fitness_val_list.append(self.get_bestFitnessValue())
        return self.fitness_val_list, self.get_bestPosition()

以上代码中，我设置的$F$为0.5，$CR$为0.8。同时在变异的代码块中对变异后的值做了边界判断，避免产生越界情况。接下来添加以下代码对DE算法进行测试，代码中，设置粒子维度为2维，种群大小即粒子个数为15，迭代次数为1000，初始的位置在（-10,10）之间

from OptAlgorithm.DE import DE
import matplotlib.pyplot as plt
import numpy as np

dim = 2
size = 15
iter_num = 1000
x_max = 10

de = DE(dim, size, iter_num, -x_max, x_max)
fit_var_list, best_pos = de.update()
print("DE最优位置:" + str(best_pos))
print("DE最优解:" + str(fit_var_list[-1]))
plt.plot(np.linspace(0, iter_num, iter_num), fit_var_list, c="G", alpha=0.5)
plt.show()

这里对2个测试函数做了测试。这两个函数在用python绘制评估优化算法性能的测试函数里都提到过，第一个是Rastrigin函数，另一个是Hölder table函数

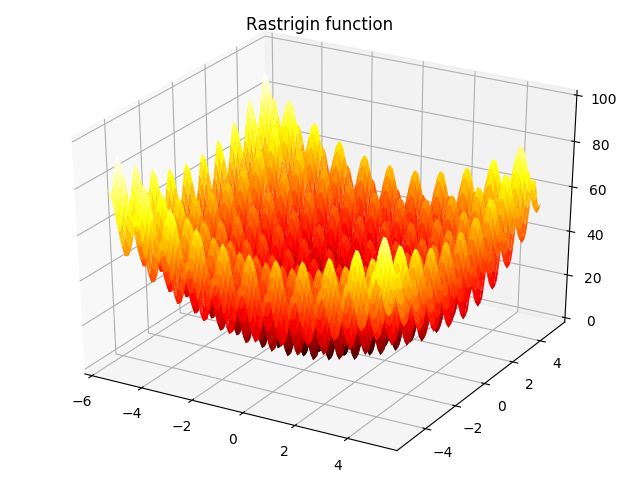
Rastrigin函数的图像如下：

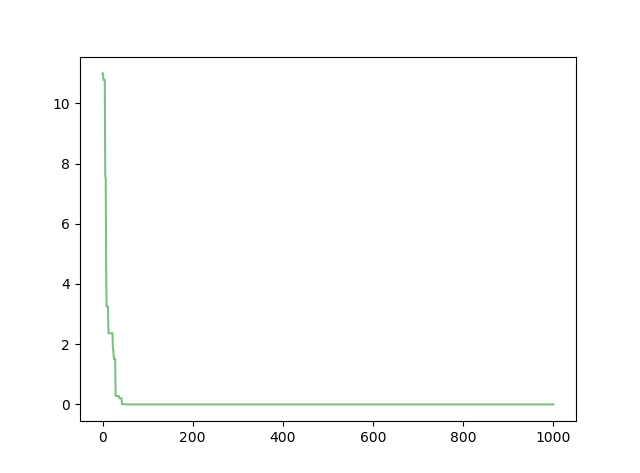
其最优解为$f(0,0,...,0)=0$。函数的收敛图像如下：

打印结果如下（可以看出此时的最优位置已经很小了，几乎为0）

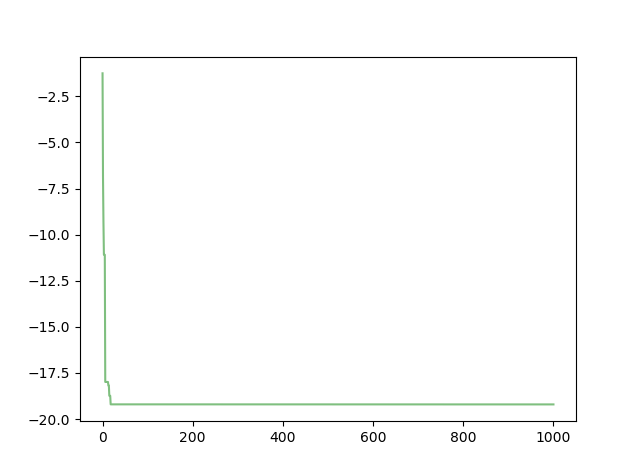
Hölder table函数的图像如下：

其解有以下四个：

函数的收敛图像如下：

打印结果如下：

此时的最优位置是4个解里的一个，且和用python3实现粒子群优化算法里的解不同。

我进行了多次试验，发现在对Hölder table函数进行测试时，DE没有陷入局部最优的情况，而PSO经常会陷入局部最优。从某种程度上说明DE在避免陷入局部最优问题上比PSO好一些。

【注】：完整源码在我的github上，找不找得到就看自己咯 ^ _ ^