矩阵乘法
矩阵相乘最重要的方法是一般矩阵 乘积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有意义
[1] 。一般单指矩阵乘积时,指的便是一般矩阵乘积。一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。由于它把许多数据紧凑的集中到了一起,所以有时候可以简便地表示一些复杂的模型。
定义
设
A为
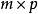 的矩阵,
B为
的矩阵,
B为
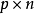 的矩阵,那么称
的矩阵,那么称
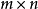 的矩阵
C为矩阵
A与
B的乘积,记作
的矩阵
C为矩阵
A与
B的乘积,记作
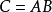 ,其中矩阵C中的第
,其中矩阵C中的第
 行第
行第
 列元素可以表示为:
列元素可以表示为:
如下所示:
注意事项
当矩阵A的列数等于矩阵B的行数时,A与B可以相乘。
-
矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
-
乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
基本性质
-
乘法结合律: ( AB) C= A( BC). [2]
-
乘法左分配律:( A+ B) C= AC+ BC [2]
-
乘法右分配律: C( A+ B)= CA+ CB [2]
-
对数乘的结合性 k( AB)=( kA) B= A( kB).
-
转置 ( AB) T= B T A T.
-
矩阵乘法一般不满足交换律 [3] 。
乘积-哈达马积( hadamard product)
乘积
Kronecker积是两个任意大小的矩阵间的运算,表示为
。克罗内克积也成为 直积或 张量积
[4] .以德国数学家利奥波德·克罗内克命名。计算过程如下例所示:
实现
C++代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
struct
Matrix:vector{
Matrix(
int
x=0,
int
y=0,
int
z=0)
//初始化,默认为0行0列空矩阵
{
assign(x,vector<
int
>(y,z));
}
int
h_size()
const
//常量说明不可省,否则编译无法通过
{
return
size();
}
int
l_size()
const
{
return
empty()?0:front().size();
//列数要考虑空矩阵的情况
}
Matrix
pow
(
int
k);
//矩阵的k次幂,用快速幂实现,k为0时返回此矩阵的单位矩阵
};
Matrix operator*(
const
Matrix &m,
const
Matrix &n)
//常量引用避免拷贝
{
if
(m.l_size()!=n.h_size())
return
Matrix();
//非法运算返回空矩阵
Matrix ans(m.h_size(),n.l_size());
for
(
int
i=0; i!=ans.h_size(); ++i)
for
(
int
j=0; j!=ans.l_size(); ++j)
for
(
int
k=0; k!=m.l_size(); ++k)
ans[i][j]+=m[i][k]*n[k][j];
return
ans;
}
Matrix Matrix::
pow
(
int
k)
{
if
(k==0)
{
Matrix ans(h_size(),h_size());
for
(
int
i=0; i!=ans.h_size(); ++i)
ans[i][i]=1;
return
ans;
}
if
(k==2)
return
(*
this
)*(*
this
);
if
(k%2)
return
pow
(k-1)*(*
this
);
return
pow
(k/2).
pow
(2);
}
|
实际应用
数据统计
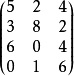
某公司有四个工厂,分布在不同地区,同时三种产品,产量(单位;t),试用矩阵统计这些数据。
| 工厂\产品 | P1 | P2 | P3 |
|---|---|---|---|
| 甲 | 5 | 2 | 4 |
| 乙 | 3 | 8 | 2 |
| 丙 | 6 | 0 | 4 |
| 丁 | 0 | 1 | 6 |
再设矩阵
,其中第一列表示三种产品的单件利润,第二列表示三种产品的单件体积。
矩阵C的第一列数据分别表示四个工厂的利润,第二列分别表示四个工厂产品需要的存储空间。
VOJ1067
我们可以用上面的方法二分求出任何一个 线性递推式的第n项,其对应 矩阵的构造方法为:在右上角的(n-1)*(n-1)的小矩阵中的 主对角线上填1,矩阵第n行填对应的 系数,其它地方都填0。例如,我们可以用下面的矩阵乘法来二分计算f(n) = 4f(n-1) - 3f(n-2) + 2f(n-4)的第k项:
利用矩阵乘法求解线性递推关系的题目有很多,这里给出的例题是系数全为1的情况。
给定一个有向图,问从A点恰好走k步(允许重复经过边)到达B点的方案数mod p的值
把给定的图转为 邻接矩阵,即A(i,j)=1当且仅当存在一条边i->j。令C=A*A,那么C(i,j)=ΣA(i,k)*A(k,j),实际上就等于从点i到点j恰好经过2条边的路径数(枚举k为中转点)。类似地,C*A的第i行第j列就表示从i到j经过3条边的路径数。同理,如果要求经过k步的路径数,我们只需要二分求出A^k即可。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
|
#include
#include
#include
#include
#include
#define N 10
using
namespace
std;
const
int
mod = 7777777;
typedef
long
long
LL;
struct
matrix{
LL a[10][10];
}origin;
int
n,m;
matrix multiply(matrix x,matrix y)
{
matrix temp;
memset
(temp.a,0,
sizeof
(temp.a));
for
(
int
i=0;i
{
for
(
int
j=0;j
{
for
(
int
k=0;k
{
temp.a[i][j]+=x.a[i][k]*y.a[k][j];
temp.a[i][j]=(temp.a[i][j])%mod;
}
}
}
return
temp;
}
matrix matmod(matrix A,
int
k)
{
matrix res;
memset
(res.a,0,
sizeof
res.a);
for
(
int
i=0;i
while
(k)
{
if
(k&1) res=multiply(res,A);
k>>=1;
A=multiply(A,A);
}
return
res;
}
void
print(matrix x)
{
for
(
int
i=0;i
{
for
(
int
j=0;j
cout<<
" "
<
}
printf
(
"---------------\n"
);
}
int
main()
{
int
k;
while
(cin>>n>>k)
{
memset
(origin.a,0,
sizeof
origin.a);
origin.a[0][0]=1;
for
(
int
i=1;i<=n;i++)
{
origin.a[i][0]=1;
for
(
int
j=0;j
origin.a[i][0]+=origin.a[j][0];
}
// print(origin);
matrix res;
memset
(res.a,0,
sizeof
res.a);
for
(
int
i=0;i
res.a[i][i+1]=1;
for
(
int
i=0;i
//print(res);
res=matmod(res,k-1);
LL fans=0;
for
(
int
i=0;i
{
fans+=res.a[0][i]*origin.a[i][0];
fans%=mod;
}
cout<
}
return
0;
}
|
经典题目9
用1 x 2的多米诺骨牌填满M x N的矩形有多少种方案,M<=5,N<2^31,输出答案mod p的结果
我们以M=3为例进行讲解。假设我们把这个矩形横着放在电脑屏幕上,从右往左一列一列地进行填充。其中前n-2列已经填满了,第n-1列参差不齐。现在我们要做的事情是把第n-1列也填满,将状态转移到第n列上去。由于第n-1列的状态不一样(有8种不同的状态),因此我们需要分情况进行讨论。在图中,我把转移前8种不同的状态放在左边,转移后8种不同的状态放在右边,左边的某种状态可以转移到右边的某种状态就在它们之间连一根线。注意为了保证方案不重复,状态转移时我们不允许在第n-1列竖着放一个 多米诺骨牌(例如左边第2种状态不能转移到右边第4种状态),否则这将与另一种转移前的状态重复。把这8种状态的转移关系画成一个有向图,那么问题就变成了这样:从状态111出发,恰好经过n步回到这个状态有多少种方案。比如,n=2时有3种方案,111->011->111、111->110->111和111->000->111,这与用多米诺骨牌覆盖3x2矩形的方案一一对应。这样这个题目就转化为了我们前面的例题8。
后面我写了一份此题的 源代码。你可以再次看到位运算的相关应用。
经典题目10
POJ2778
题目大意是,检测所有可能的n位DNA串有多少个DNA串中不含有指定的病毒片段。合法的DNA只能由ACTG四个字符构成。题目将给出10个以内的病毒片段,每个片段长度不超过10。数据规模n<=2 000 000 000。
下面的讲解中我们以ATC,AAA,GGC,CT这四个病毒片段为例,说明怎样像上面的题一样通过构图将问题转化为例题8。我们找出所有病毒片段的前缀,把n位DNA分为以下7类:以AT结尾、以AA结尾、以GG结尾、以?A结尾、以?G结尾、以?C结尾和以??结尾。其中问号表示“其它情况”,它可以是任一字母,只要这个字母不会让它所在的串成为某个病毒的前缀。显然,这些分类是全集的一个划分(交集为空, 并集为全集)。现在,假如我们已经知道了长度为n-1的各类DNA中符合要求的DNA个数,我们需要求出长度为n时各类DNA的个数。我们可以根据各类型间的转移构造一个边上带权的有向图。例如,从AT不能转移到AA,从AT转移到??有4种方法(后面加任一字母),从?A转移到AA有1种方案(后面加个A),从?A转移到??有2种方案(后面加G或C),从GG到??有2种方案(后面加C将构成病毒片段,不合法,只能加A和T)等等。这个图的构造过程类似于用 有限状态自动机做串匹配。然后,我们就把这个图转化成 矩阵,让这个矩阵自乘n次即可。最后输出的是从??状态到所有其它状态的路径数总和。
题目中的数据规模保证前缀数不超过100,一次矩阵乘法是三方的,一共要乘log(n)次。因此这题总的 复杂度是100^3 * log(n),AC了。
最后给出第9题的代码供大家参考(今天写的,熟悉了一下C++的类和运算符重载)。为了避免大家看代码看着看着就忘了,我把这句话放在前面来说:
Matrix67原创,转贴请注明出处。
[5]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
#include
#define SIZE (1<#define MAX_SIZE 32
using
namespace
std;
class
CMatrix
{
public
:
long
element[MAX_SIZE][MAX_SIZE];
void
setSize(
int
);
void
setModulo(
int
);
CMatrix operator* (CMatrix);
CMatrix power(
int
);
private
:
int
size;
long
modulo;
};
void
CMatrix::setSize(
int
a)
{
for
(
int
i=0; i
for
(
int
j=0; j
element[i][j]=0;
size = a;
}
void
CMatrix::setModulo(
int
a)
{
modulo = a;
}
CMatrix CMatrix::operator* (CMatrix param)
{
CMatrix product;
product.setSize(size);
product.setModulo(modulo);
for
(
int
i=0; i
for
(
int
j=0; j
for
(
int
k=0; k
{
product.element[i][j]+=element[i][k]*param.element[k][j];
product.element[i][j]%=modulo;
}
return
product;
}
CMatrix CMatrix::power(
int
exp
)
{
CMatrix tmp=(*
this
)*(*
this
);
if
(
exp
==1)
return
*
this
;
else
if
(
exp
&1)
return
tmp.power(
exp
/2)*(*
this
);
else
return
tmp.power(
exp
/2);
}
int
main()
{
const
int
validSet[]={0,3,6,12,15,24,27,30};
long
n, m, p;
CMatrix unit;
scanf
(
"%d%d%d"
, &n, &m, &p);
unit.setSize(SIZE);
for
(
int
i=0; i
for
(
int
j=0; j
if
(((~i)&j) == ((~i)&(SIZE-1)))
{
bool
isValid=
false
;
for
(
int
k=0;k<8;k++) isValid=isValid||(i&j)==validSet[k];
unit.element[i][j]=isValid;
}
unit.setModulo(p);
printf
(
"%d"
,unit.power(n).element[SIZE-1][SIZE-1] );
return
0;
}
|
矩阵乘法例题
vijos1049
题目大意是给你一个物品变换的顺序表,然后让你求变换了n次之后物品的位置.
解析:这个题目仔细想想并不是很难,由于每一行的变换顺序是不一样的,我们需要把所给出的矩阵每一行的变换用一个矩阵乘法维护,然而如果每次都乘一下的话就很容易超时.所以我们可以将每一行的变换得到的矩阵全部乘起来得到一个新矩阵,它就是变换k次(k是所给矩阵的行数)所乘的矩阵,那么我们就可以使用快速幂了,对于余数就暴力算就可以啦.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
#include
#include
#include
using
namespace
std;
static
const
int
maxm=1e2+10;
#define REP(i,s,t) for(int i=s;i<=t;i++)
typedef
long
long
LL;
struct
matrix{
LL mtx[maxm][maxm];
}mx[16];
LL n,k,m;
LL A[maxm][maxm];
matrix mul(matrix A,matrix B){
matrix ret;
memset
(ret.mtx,0,
sizeof
ret.mtx);
REP(i,1,n)REP(j,1,n)REP(k,1,n)
ret.mtx[i][j]=(ret.mtx[i][j]+A.mtx[i][k]*B.mtx[k][j]);
return
ret;
}
matrix
pow
(matrix A,LL n){
if
(!n)
return
A;
matrix ret=A;n--;
while
(n){
if
(n&1)ret=mul(ret,A);
A=mul(A,A);
n>>=1;
}
return
ret;
}
void
display(matrix base){
for
(
int
i=1;i<=n;i++)
printf
(
"%lld "
,base.mtx[1][i]);
puts
(
""
);
}
int
main(){
matrix st,get,f;
scanf
(
"%lld%lld%lld"
,&n,&m,&k);
for
(
int
i=1;i<=m;i++){
for
(
int
j=1;j<=n;j++){
scanf
(
"%lld"
,&A[i][j]);
mx[i].mtx[A[i][j]][j]=1;
}
}
for
(
int
i=1;i<=n;i++)st.mtx[1][i]=i;
get=mx[1];
for
(
int
i=2;i<=m;i++)get=mul(get,mx[i]);
get=
pow
(get,k/m);k%=m;
for
(
int
i=1;i<=k;i++)get=mul(get,mx[i]);
st=mul(st,get);
display(st);
return
0;
}
//by Exbilar
|