《大话数据结构》笔记：第六章
目录
- 六、树
- 6.1.1 度（Degree）
- 6.2.2节点间关系
- 6.2.3 其他概念
- 6.3 具体操作
- 6.4树的存储结构
- 6.4.1父节点表示法
- 6.4.2 子节点表示法
- 6.4.2 兄弟节点表示法
- 6.5二叉树（重点）
- 6.5.1特点
- 6.5.2 特殊二叉树
- 6.6二叉树的特性
- 6.7二叉树存储结构
- 6.7.1顺序存储结构
- 6.7.2二叉链表
- 6.8遍历二叉树
- 前序遍历
- 中序
- 后序
- 层序
- 6.9建立二叉树
- 6.10线索二叉树
- 6.11树，森林与二叉树的转换
- 6.11.1树转二叉树
- 6.11.2森林转二叉树
- 6.11.3二叉树转树
- 6.11.4二叉树转森林
- 6.11.5 树与森林的遍历
- 6.12赫夫曼树
六、树
有且仅有一个根节点（root），连接多个地址，每个地址都应一棵子树。子树相互独立，无交叉。
6.1.1 度（Degree）
结点拥有的子树数称为节点的度（Degree）。度为0的节点是叶节点（Leaf）或终端节点。反之称为非终端节点，或分支节点。除根节点，也称为内部节点。树的度是各节点的度的最大值。
6.2.2节点间关系
父（Parent），子（Child），兄弟（Sibling），祖先，子孙
6.2.3 其他概念
节点的层次（Level）：根在第一层，子节点在第二层，依次往下。
树的深度（Depth）或高度：树中节点最大层次
有序树/无序树：树中节点各子树是否有顺序
森林（Forest）：几颗互不相交的树。树的两颗子树可以称为森林。
线性结构和树结构：
6.3 具体操作
操作：构建树，销毁树。。
#这个还是根据python具体去了解，c语言的不通用
6.4树的存储结构
三种表示方法:双亲，孩子表示法，孩子兄弟表示法。
（翻译成双亲实在不好理解，应该是父节点表示法）
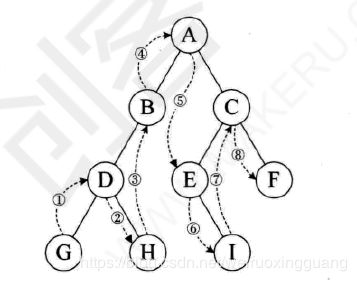
6.4.1父节点表示法
每个节点包括：数据域和指针域，指针指向父节点在数组中的下标。
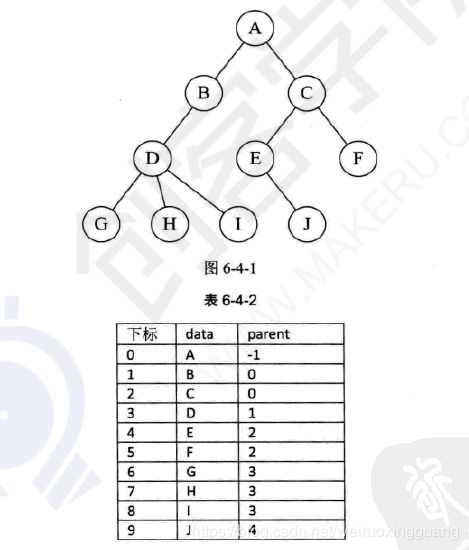
容易找到父节点，O(1)，找子节点，需要遍历整棵树。
改进：
两个指针，一个指向父节点，一个指向第一个子节点。
或者一个指向父节点，一个指向右兄弟节点，
针对不同需求，有各种各样的结构。
6.4.2 子节点表示法
多个指针，每个指针指向一个子节点。
#二叉树通常是子节点表示法。
方案一
每个节点都带n个指针，n是树的度，即所有节点中的最大分叉数。分叉不够的节点数，补足空指针。
缺点：
节点分叉差别很大时，浪费空间
方案二
每个节点先记录分叉数，或者叫度（degree），在带上degree个指针。
缺点：
各节点结构不同，需要更新分叉数，时间运算慢
方案三
各分叉之间用链表相连：
首先是data和firstchild指针，指针指向第一个子节点。然后各子节点之间用链表相连，child和 next。
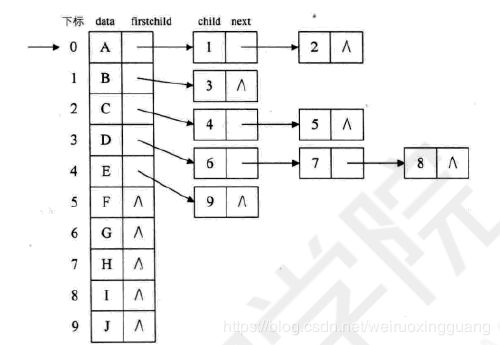
缺点：
还是需要遍历这个结构才能得到父节点
方案四 :父子节点表示法
data + parent + firstchild,加上父节点的指针
6.4.2 兄弟节点表示法
data +两个指针，一个是第一个子节点，一个是它的右边节点
特点：方便找子节点，找父节点可以加parent指针。
重点是转为了二叉树。
#这个转换感觉很重要，直接将任意形式的多叉树转为了二叉树进行处理。
#但应该还需要记录原来的格式，这个应该不能恢复原多叉树的。因为有多种可能。比如一条单链，你不知道这原来就是单链，还是父节点和多个子节点。
6.5二叉树（重点）
二叉树（Binary Tree）是一个根节点，和两颗互不相交的左子树/右子树的二叉树组。（非空状态下）
6.5.1特点
1.最多两个子树，度最大为2，可以有一个子树或没有。
2.左右子树有顺序，不能颠倒。
3.一颗子树，也要分为左子树还是右子树。
二叉树的五种形态：
1.空树
2.只有根节点
3.只有左子树
4.只有右子树
5.左右子树都有
三个节点的树：有五种
6.5.2 特殊二叉树
1.斜树：只有一个节点，分左斜/右斜。节点树等于树的深度，简单说就是链表。
2.满二叉树：
所有分支都存在左右子树，且叶子节点在同一层。
3.完全二叉树：
完全二叉树的特点:
#感觉深度最小的特性比较有用，即满排树。
6.6二叉树的特性
1.第n层最多2n-1个节点。
2.深度为k，最多2k-1个节点。
3.叶子节点个数是双分叉节点加1。
证明：
总节点数是n，叶子节点n0，单分叉节点（度）n1，双分叉节点n2。
n = n0+n1+n2
除了根节点，每个节点都对应一根连接线，所以线数是n-1。
而另一个角度看，双分叉两根线，单分叉一根线，
所以
n-1 = n1+2*n2
所以。n0 = n2+1。
4.n个节点的完全二叉树的深度为[log2n]+1
5.n个节点的完全二叉树。第i个节点。
if i== 1：i是根节点。
else: 其父节点是i//2，i 整除2的结果。
如果 2i>n，i 节点是叶子节点，否则其左子节点是2i
如果2i+1 >n， i 节点无右孩子，否则，其右孩子是2i+1
6.7二叉树存储结构
6.7.1顺序存储结构
完全二叉树适合顺序存储，其他类型会造成空间浪费。
#其实这就是刷题时给的数组形式的二叉树，有空时补null。
6.7.2二叉链表
数据域加两个指针域
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
6.8遍历二叉树
二叉树的遍历：从根节点出发，按照某种次序依次访问二叉树的所有节点，每个节点被访问一次并仅被访问一次。
前序遍历
根—左子树—右子树
中序
左子树—根---右子树
后序
左子树—右子树—根
层序
每层结束后，访问下一层
已知前序和中序，或者后序和中序是可以确定一棵二叉树。
但只有前序和后序，无法确定。
6.9建立二叉树
拓展二叉树：
二叉树的每个节点的空指针，引出一个虚节点。比如其值为“#”。
#M，回头看一下python递归建树的代码
6.10线索二叉树
空指针数：n个节点的二叉树，一共2n个指针，n-1个分支线数，所有存在2n-（n-1）=n+1个空指针。所以会很浪费空间。
线索二叉树：指向前驱和后继的指针称为线索，加上线索的二叉链表称为线索链表，相应二叉树称为线索二叉树。
总结来说：所有节点的左指针，指向中序遍历上一个，右指针，指向中序遍历的下一个。形成一个中序遍历顺序的双向链表。
其实就是把中序遍历的list转为双向的链表。
#相比于中序遍历有什么优势，并未说明。
同时为了分辨两个指针，用两个布尔值区分前驱和后继指针。
优势：如果所用二叉树，经常遍历或查找，需要前驱和后继，那么用线索二叉树的存储结构，能够节省空间和时间。
#相应代码python
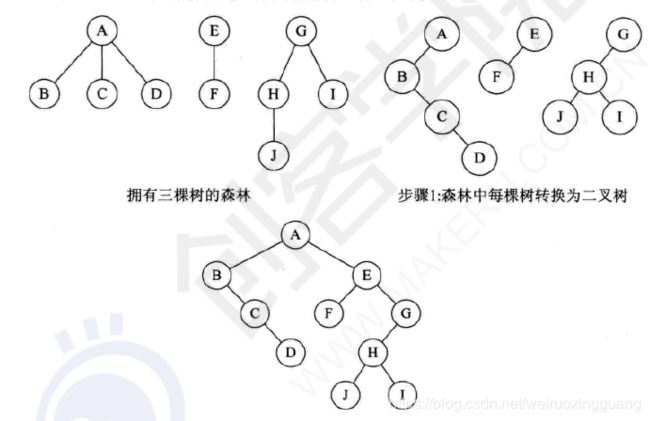
6.11树，森林与二叉树的转换
6.11.1树转二叉树
1.加线：树的兄弟节点之间，加线。
2.去线：每个节点，只保留和第一个子节点的连线，去掉和其他子节点的连线。
3.层次调整：子节点是左子树，兄弟节点是右子树。
6.11.2森林转二叉树
将所有树的根节点，视为兄弟节点。
6.11.3二叉树转树
反过来，右子树都是兄弟节点，左子树，是子节点。
6.11.4二叉树转森林
根节点有右子树，即有兄弟节点，那就是森林。
6.11.5 树与森林的遍历
树的遍历：先根遍历/后根遍历
森林的遍历：前序遍历/后序遍历
#森林的后序是二叉树的中序，因为根节点是第一棵树的。
6.12赫夫曼树
压缩编码方法：赫夫曼编码
多次分数分类问题
路径长度：树中一个节点到另一个节点，的分叉线数。
数的路径长度：根节点到所有节点（不仅是叶子，所有节点）的路径长度之和。
其中左面树路径长度20，右面是16。
带权的节点：每个叶子节点路径长度与权的乘积之和。
其中带权路径长度WPL的最小二叉树称作赫夫曼树（最优二叉树）。
#感觉就是前n-1层满排的二叉树，因为最后一层不一定从最前面开始，不一定是完全二叉树，但是很接近。后面发现好像也不对，权重低的会尽量远离根节点。
构建赫夫曼树：
1.所有权值的子节点从小到大排序。
2.最小的两个做为左右节点，形成树。小的在左，根是两者之和。把两者之和的根节点，放进排序。
3.重复这一流程。
#与现实不同，未必是最优情况。
赫夫曼编码问题
实例：
解码：
前缀编码：任何一个字符的编码，都不是另一个字符编码的前缀，避免混淆。
赫夫曼编码本身就是前缀编码。