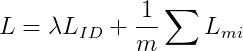Re-ID ——表征学习和度量学习

表征学习

将行人重识别问题作为分类问题和验证问题。

1.分类问题

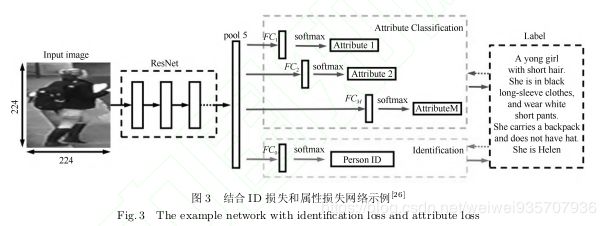
分类标准：一般是多个结合起来的，即：ID损失+多个属性（如：颜色等）损失的均值

损失函数：

网络结构：

2.验证问题：输入两张图片来判断它们是不是同一张图片

具体：输入两张图片，经过同一个CNN,得到两个特征向量，将两个特征向量融合起来到FC层，最后输出只有两个神经元的FC,用以判断是否是同一行人。

损失函数：(这个加和只有两个项)。

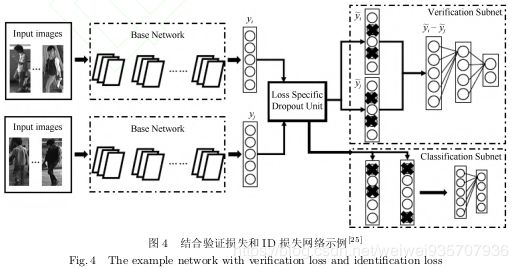
3.其实一般是不会单独使用验证网络，而是将验证网络和分类网络结合起来：

损失函数：

网络图：

---

度量学习

背景：度量学习通常应用在图像检索领域

目的：通过网络学习出两张图片的相似度

做法：输入两张图片，通过网络向前传播归一化后得到特征向量，计量特征间距离，通过距离损失优化网络。

           目标：正样本对间的距离尽可能小而负样本对间的距离尽可能大。

           距离度量：

                             1）为实现端对端训练，度量函数尽量连续可导。

                             2）常使用归一化特征欧式距离，或者特征的余弦距离。

                                   欧式距离：

                                   余弦距离：

                             3) 汉明距离，马式距离，曼哈顿距离也可以作为距离度量。

对比损失：

                目的：训练孪生网络

                输入：一对图片，同一行人（y==1）或者不同行人(y==0)

                损失函数：

                                解释：

                                         1）更具y分同一张图片和不同图片计算距离

                                         2）表示         

                                         3) 是超参，更具具体训练情况而定。

三元组损失：

                输入：三张图片，即固定样本，正样本，负样本

                损失函数：

                改进的损失函数：  因为有人认为，前者只考虑了正负样本对之间的相对距离。目的：把正负样本对推开（？一个减小，一个增大就是推开吗），减小正样本对之间的距离。

四元组损失：

             输入：四章图片，即固定样本，正样本，负样本2个

             损失函数：    （前称为强推动项，后称为弱推动项）

             解释：在将正负样本对推开的同时很难保证固定样本和正样本间的距离，会影响固定样本本身（？），三元组损失加入如上项解决，而四元组通过再加一个负样本解决。是手动设置的正常数，且前者比后者大。

难样本采样：

             做法：非常不像的正样本和非常像的负样本。

             作用：提高模型泛化能力，加快收敛速度，方便使用。

---

总结：

    1.二者差别：表征学习相当于特征空间的分界面，表征学习相当于特征空间的聚类。

    2.度量学习优势：比起表征学习不需要全链接层，因此对于ID的数量不敏感。

    3.趋势：将二者结合起来。