静电能
点电荷之间的相互作用能
把一堆点电荷聚在一起需要做多少功?
先把一个点电荷\(q_1\)放在某处,然后将第二个点电荷\(q_2\)从无限远处移动至距离\(q_1\) \(r_{12}\)处,外力做功:
\begin{equation*} A_2'=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r_{12}}=q_2U_{12} \end{equation*}
其中\(U_{12}\)为点电荷\(q_1\)的电场在点电荷\(q_2\)处的电势。
再移动过来点电荷\(q_3\),外力做功:
\begin{equation*} A_3'=\frac{1}{4\pi\varepsilon_0}\left(\frac{q_1q_2}{r_{13}}+\frac{q_2q_3}{r_{23}}\right)=q_2\left(U_{13}+U_{23}\right) \end{equation*}
以此类推,把第\(i\)个点电荷移动过来,需要做功:
\begin{equation*} \begin{split} A_i'=&\frac{1}{4\pi\varepsilon_0}\left(\frac{q_1q_i}{r_{1i}}+\frac{q_2q_i}{r_{2i}}+\dots+\frac{q_{i-1}q_i}{r_{i-1,i}}\right)=\frac{1}{4\pi\varepsilon_0}\sum_j^{i-1}\frac{q_iq_j}{r_{ij}}\\ =&q_i\sum_j^{i-1}U_{ij}=q_iU_i \end{split} \end{equation*}
把\(n\)个电荷都摆在相应的位置,需要做功
\begin{equation*} \begin{split} A'=&\sum_{i=2}^n A_i'=\frac{1}{4\pi\varepsilon_0}\sum_{i=2}^n \sum_{j=1}^{i-1}\frac{q_iq_j}{r_{ij}}=\frac{1}{4\pi\varepsilon_0}\sum_{i=1}^n \sum_{j=1}^{i-1}\frac{q_iq_j}{r_{ij}}\\ =&\sum_{i=1}^nq_i\sum_{j=1}^{i-1}U_{ij} \end{split} \end{equation*}
如果先把第\(n\)个电荷放置好,然后依次放置第\(n-1\)、\(n-2\)、\(\dots\)、\(1\)个电荷,则需要做功
\begin{equation*} A''=\frac{1}{4\pi\varepsilon_0}\sum_{i=1}^n \sum_{j=i+1}^{n}\frac{q_iq_j}{r_{ij}} =\sum_{i=1}^nq_i\sum_{j=i+1}^{n}U_{ij} \end{equation*}
显然\(A'=A''\),则\(A'\)还可写为:
\begin{equation*} A'=\frac{1}{2}(A'+A'')=\frac{1}{8\pi\varepsilon_0}\sum_{i=1}^n \sum_{j=1,j\neq i}^{n}\frac{q_iq_j}{r_{ij}} =\frac{1}{2}\sum_{i=1}^nq_i U_{i} \end{equation*}
外力做功转化为点电荷系的相互作用能\(W_{互}\):
\begin{equation*} W_{互}=\frac{1}{8\pi\varepsilon_0}\sum_{i=1}^n \sum_{j=1,j\neq i}^{n}\frac{q_iq_j}{r_{ij}} =\frac{1}{2}\sum_{i=1}^nq_i U_{i} \end{equation*}
点电荷系的相互作用能等于各点电荷电量与该电荷所在处电势乘积之和的一半。
如果电荷系处于某静电场中,则电荷系的静电能为:
\begin{equation*} W_{e}=\sum_iq_iU_{0i}+\frac{1}{2}\sum_{i=1}^nq_i U_{i} \end{equation*}
其中,\(U_{0i}\) 为\(q_i\) 处外电场的电势,第一项为电荷系在外场中的静电能。
电荷连续分布带电体的电势能
连续带电体可以分割成很多的电荷元,每个电荷元\(\mathrm dq\)可以看成点电荷,则带电体静电能为:
\begin{equation*} W_{e}=\frac{1}{2}\int U\mathrm dq \end{equation*}
对于体分布:
\begin{equation*} W_{e}=\frac{1}{2}\int U\rho\mathrm dV \end{equation*}
对于面分布:
\begin{equation*} W_{e}=\frac{1}{2}\int U\sigma \mathrm dS \end{equation*}
对于线分布:
\begin{equation*} W_{e}=\frac{1}{2}\int U\eta\mathrm dl \end{equation*}
如果只有一个带电体,以上各式就是各带电体的自能。
例1 3个点电荷,放在边长为\(l\) 的等边三角形的三个顶点上,求体系的静电能。
三个顶点处电势为 \(U_1=U_2=U_3=\frac{q}{4\pi\epsilon_0l}+\frac{q}{4\pi\epsilon_0l}=\frac{q}{2\pi\epsilon_0l}\),静电能为
\begin{equation*} W_{e}=\frac{1}{2}\sum_iq_iU_i=\frac{3q}{2}\frac{q}{2\pi\epsilon_0l}=\frac{3q^2}{4\pi\epsilon_0l} \end{equation*}
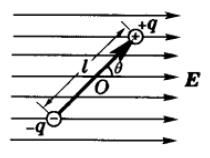
例2 电偶极子在均匀电场中的静电能
电偶极子电势能
\begin{equation*} W=-qU_-+qU_+=q(U_+-U_-)=-qEl\cos\theta=-\vec{p}\cdot\vec{E} \end{equation*}
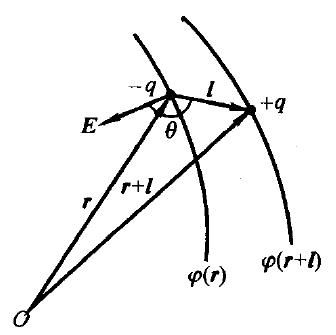
例3 电偶极子在电场中的静电能
外场的电势分布为\(U(\vec{r})\)。电偶极子负电荷位于\(\vec{r}\)处,则正电荷位于\(\vec{r}+\vec{l}\)处,电偶极子电势能
\begin{equation*} W=-qU(\vec{r})+qU(\vec{r}+\vec{l})=q\vec{l}\cdot\nabla U(\vec{r})=-\vec{p}\cdot\vec{E} \end{equation*}
例4 求均匀带点球的自能。球半径为\(R\),电量为\(Q\)。
电荷体密度为
\begin{equation*} \rho=\frac{3Q}{4\pi R^3} \end{equation*}
根据高斯定理,可求得电场分布
\begin{equation*} \vec{E}(\vec{r})= \begin{cases} \frac{\rho}{3\epsilon_0}\vec{r}, & r\lt R \\ \frac{Q}{4\pi\epsilon_0 r^2}\hat{r}, & r \gt R \end{cases} \end{equation*}
球内任意一点电势
\begin{equation*} \begin{split} U(r)=&\int_r^{\infty}E(r)\mathrm dr=\int_r^R\frac{\rho}{3\epsilon_0}\mathrm dr+\int_R^{\infty}\frac{Q}{4\pi\epsilon_0 r^2}\mathrm dr \\ =&\frac{\rho}{6\epsilon_0}(3R^2-r^2) \end{split} \end{equation*}
静电能
\begin{equation*} W_{e}=\frac{1}{2}\int U\rho\mathrm dV=\frac{\rho^2}{12\epsilon_0}\int_0^R(3R^2-r^2)4\pi r^2\mathrm dr=\frac{3}{5}\frac{Q^2}{4\pi\epsilon_0R^2} \end{equation*}
这就是带电球的自能。若带电球半径\(R\rightarrow 0\),自能\(W\rightarrow \infty\),发散,这显然好不符合物理的。电子是最小的带电体,若把电子看成点电荷,将会有发散的困难,为了避免此困难,必须假定电子的电荷在一定范围内分布。
导体
静电平衡
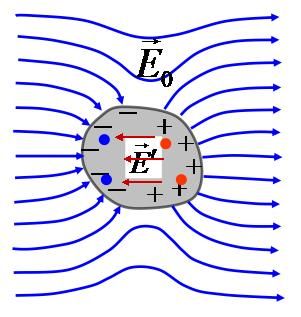
导体内有大量自由电子,自由电子在电场力作用下运动使电荷在导体上重新分布,这种现象称为导体的静电感应现象。感应电荷产生的电场称为附加电场。如图1所示,当电场中引入导体后,空间的电场分布发生变化:
\begin{equation*} \vec{E}=\vec{E}_0+\vec{E}' \end{equation*}
其中,\(\vec{E}_0\)为外电场,\(\vec{E}'\)为导体上的感应电荷产生的附加电场。
当导体内部的电场\(\vec{E}=0\)时,导体内部没有宏观电荷移动,称导体达到了静电平衡,如图2所示
(a) 在外电场\(\vec{E}_0\)作用下,电子逆电场方向运动;
(b) 导体表面出现感应电荷,导体内产生附加电场\(\vec{E}'\) ;
(c) 当导体内的外电场\(\vec{E}_0\)与附加电场\(\vec{E}'\)等值而反向时,电荷运动停止,导体处于静电平衡状态。
当导体处于静电平衡时,可导出如下推论:
- 导体是个等势体,导体表面是个等势面。
- 导体表面附近处的场强与表面垂直。
导体上电荷分布
(1) 实心导体内部无电荷
图3 实心导体
可由高斯定理证明,在实心导体内部做个任意的高斯面,\(\oint_S\vec{E}\cdot\mathrm d\vec{S}=q_{内}/\varepsilon_0=0\),所以\(q_{内}=0\)。
(2) 空腔导体(内部无带电体)导体内和空腔内表面均无电荷
对于空心导体,如果空腔内没有带电体,则导体内表面处处无电荷分布,电荷只能分布在外表面,空腔内电势处处相等,没有电场。
图4 空腔导体(内部无带电体)
由高斯定理可以证明空腔内表面没有净电荷,还可以证明:导体空腔的内表面上也不可能有等量异号电荷。若腔内表面有等量异号电荷出现,则空腔内必有电场线存在(见图4),将试探电荷\(q_0\)沿该电场线由正电荷移到负电荷时,电场力的功不为零,这与静电平衡时导体是等势体的结论不符。
(3) 空腔导体(内部有带电体)
图5 空腔导体(内部有带电体)
由高斯定理,易证电荷分布在导体内、外两个表面,其中内表面的电荷是空腔内带电体的感应电荷, 与腔内带电体的电荷等量异号。
(4) 导体面电荷密度与场强
图6 导体表面做高斯面
在导体表面取很薄的柱状高斯面,如图6所示,则其侧面和导体内底面的电通量为零,则
\begin{equation*} \oint_S\vec{E}\cdot\mathrm d\vec{S}=E\Delta S = \frac{\sigma \Delta S}{\varepsilon_0} \end{equation*}
于是可得
\begin{equation*} E = \frac{\sigma }{\varepsilon_0} \end{equation*}
可见,$E\varpropto \frac{1}{\rho} $,导体表面曲率半径小的地方,电场强度大。针尖状导体处电场很强,可使周围的空气电离,同时产生“电风”,称为尖端放电。
(5) 静电屏蔽
图7 对腔外电场的屏蔽
空腔导体(不论是否接地)的内部空间不受腔外电荷和电场的影响;接地的空腔导体, 腔外空间不受腔内电荷和电场的影响。
图8 对腔内电场的屏蔽
电容
一个孤立导体,带有电量\(q\),电势为\(U\),二者成正比,比例系数\(C=q/U\)称为导体的电容。导体的电容与导体的形状和尺寸有关,是导体本身的性质,与电量无关。电容表示使导体升高单位电势所需要的电量。国际单位制中,电容的单位是\(\mathrm{C/V}\),有个专门的名称,叫做法拉,符号\(\mathrm F\)。注意不要与另外一个单位法拉第相混淆,法拉第是电量的单位,表示1摩尔电子的电量,即96485\(\mathrm{C}\)。
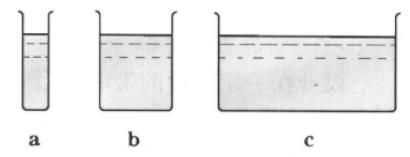
电容可以与水容器类比。不同的容器,使水面上升一个单位高度,所需要的水量不同,即“水容”不同,“水容”与容器形状无关,与是不是有水无关。
对于孤立导体球,\(U=\frac{q}{4\pi\varepsilon_0 R}\),电容 \(C=\frac{q}{U}=4\pi\varepsilon_0 R\)。
电容器及其电容
带等量异号电荷的两个导体(称为极板)组成的系统称为电容器。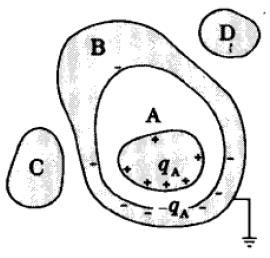
图10 电容器
电容器的电容定义为:
\begin{equation*} C = \frac{Q}{U_A-U_B} =\frac{Q}{U_{AB}} \end{equation*}
当周围电荷分布或电介质分布发生变化时,电容C也发生变化。但当电容器一极板包围另一极板或两平行极板相距很近时,电场将只分布在两极板之间且不受周围情况的影响,使极板间电势差保持稳定。此时,电容器的电容只决定于其本身的结构。
以下讨论几种形状简单、对称的电容器的电容。
(1) 平行板电容器
图11 平行板电容器
\begin{equation*} U_{AB}=Ed=\frac{\sigma d}{\varepsilon_0}=\frac{Q d}{S\varepsilon_0} \end{equation*}
\begin{equation*} C = \frac{Q}{U_{AB}} = \frac{\varepsilon_0 S}{d} \end{equation*}
(2) 球形电容器
图12 球形电容器
两极板间的电场:
\begin{equation*} \vec{E}=\frac{1}{4\pi\varepsilon_0}\frac{Q}{r^2}\hat{r} \end{equation*}
两极板间电势差:
\begin{equation*} U_{AB}=\int_{R_A}^{R_B}E\mathrm dr=\frac{Q}{4\pi\varepsilon_0}\frac{R_B-R_A}{R_AR_B} \end{equation*}
电容:
\begin{equation*} C = \frac{Q}{U_{AB}} = \frac{4\pi\varepsilon_0 R_AR_B}{R_B-R_A} \end{equation*}
(3) 圆柱形电容器
图12 圆柱形电容器
两极板间的电场:
\begin{equation*} \vec{E}=\frac{1}{2\pi\varepsilon_0}\frac{\lambda}{r}\hat{r} \end{equation*}
两极板间电势差:
\begin{equation*} U_{AB}=\int_{R_A}^{R_B}E\mathrm dr=\frac{\lambda}{2\pi\varepsilon_0}\ln\frac{R_B}{R_A}=\frac{Q}{2\pi\varepsilon_0 l}\ln\frac{R_B}{R_A} \end{equation*}
电容:
\begin{equation*} C = \frac{Q}{U_{AB}} = \frac{2\pi\varepsilon_0 l}{\ln(R_B/R_A)} \end{equation*}
静电场的能量
带电导体的静电能
对于带电导体,电荷都分布在表面上,整个导体是个等势体,导体系的静电能:
\begin{equation*} W = \frac{1}{2}\int_S \sigma U \mathrm dS=\frac{1}{2}\sum_{i=1}^n U_i \int_{S_i} \sigma \mathrm dS_i = \frac{1}{2}\sum_{i=1}^n Q_i U_i \end{equation*}
其中,\(Q_i\) 为第\(i\) 个导体的电量,\(U_i\) 为第\(i\) 个导体的电势。
电容器是两个导体极板组成的导体系,两个极板电量分别为\(\pm Q\),电势分别为\(U_1\)和\(U_2\),电容器能量为:
\begin{equation*} W = \frac{1}{2}\sum_{i=1}^n Q_i U_i = \frac{1}{2}Q(U_1-U_2)=\frac{1}{2}QU=\frac{1}{2}CU^2=\frac{1}{2}\frac{Q}{C^2} \end{equation*}
不难证明,电容器的能量在数值上等于电容器在充电过程中外力反抗电场力所做的功。电容器不仅是电荷的容器,还是静电能的容器。
静电场的能量
我们前面求了各种静电能的表达式,能量都与带电体的电量相联系,因此,有人认为静电能是集中在电荷上的。其实,我们只是求了电荷系的静电能,并未涉及静电能的分布。
对于平行板电容器,静电能为:
\begin{equation*} W = \frac{1}{2}CU^2=\frac{1}{2}\varepsilon_0E^2Sd \end{equation*}
可见,静电能不仅与电场强度有关,而且还与电场分布的空间体积\(Sd\)有关,这似乎表明静电能分布在电场不为0的地方,凡是有电场的地方便有静电能。静电能究竟是集中在电荷上还是分布在电场中,这个问题需要由实验来回答。在静电学范围内,这两种观点无法分辨。对于随时间变化的电场,电场可以脱离电荷而存在,并以有限的速度携带者能量在空间传播,所以说,电场是电能的携带者。
参考资料
- 苏州大学基础物理网上课堂
- 耶鲁大学《基础物理II》
- 贾启民《电磁学》