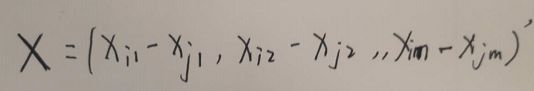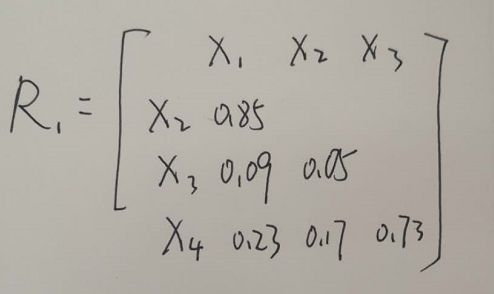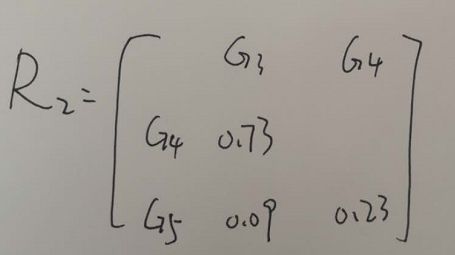博客上看到的,叫做层次聚类,但是《医学统计学》上叫系统聚类(chapter21)
思想很简单,想象成一颗倒立的树,叶节点为样本本身,根据样本之间的距离(相似系数),将最近的两样本合并到一个根节点,计算新的根节点与其他样本的距离(类间相似系数),距离最小的合为新的根节点。以此类推
对于样本X=(x1,x2,,,xm),共n个样品,m个特征,我们可以考虑两种情形聚类
R型聚类:m个特征之间的聚类,可以理解为一种降维。
Q型聚类:n个样品之间的聚类,这就是一般意义上机器学习中的系统聚类
(文中的下标i、j在R型、Q型中的含义不一样,聪明的读者自行分辨)
相似系数:
R型(真正意义上的相似系数)(r)
$r_{ij}=\frac{\left | \sum \left ( X_{i}-\bar{X_{i}} \right )\left ( X_{j}-\bar{X_{j}} \right ) \right |}{\sqrt{\sum \left ( X_{i}-\bar{X_{i}} \right )^{2}\sum \left ( X_{j}-\bar{X_{j}} \right )^{2}}}$
可以看到$r_{ij}$越大标明两特征相似程度越高
Q型(真正意义上的样品距离)(d)
闵可夫斯基(Minkowski)距离:
$\sqrt[p]{\left | x-\mu _{i} \right |^{p}}$
Minkowski距离没有考虑变量之间的相关关系。引进马氏距离:
$d_{ij}={\mathbf{X}}'\mathbf{S}^{-1}\mathbf{X}$
其中
$X=(X_{i1}-X_{j1} \right , X_{i2}-X_{j2} \right, X_{im}-X_{jm})$(不明原因的公式不正确显示)
类间相似系数:
最大相似系数法
r=Max(r)
D=Min(d)
最小相似系数法
r=Min(r)
D=Max(d)
可以看出,就是人为规定了,当某两个指标或样品合并后,新的样本(或指标)与上一节点样品(或指标)的距离(或相似系数)的选取
现举实例说明
测量了300名成年女子身高(X1)、下肢长(X2)、腰围(X3)、胸围(X4)
得到相似系数矩阵
可以看到X1,X2的相似系数最大,所以将X1,X2合并为G5
X3变为G3,X4变为G4
G3与G4的相似系数不变,为0.73
G5与G3、G5与G4的类间相似系数采用最大相似系数法
G5与G3的类间相似系数r = Max r
即$r_{53}=Max(r_{13},r_{23})=Max(0.09,0.05)=0.09$
$r_{54}=Max(r_{14},r_{24})=Max(0.23,0.17)=0.23$
所以有
根据上述步骤,直到所有的类都归为一类。
在R2中可知,G3、G4的相似系数最大,将他们归为G6,由此我们得到身高与下肢长为一类G5,腰围与胸围一类G6
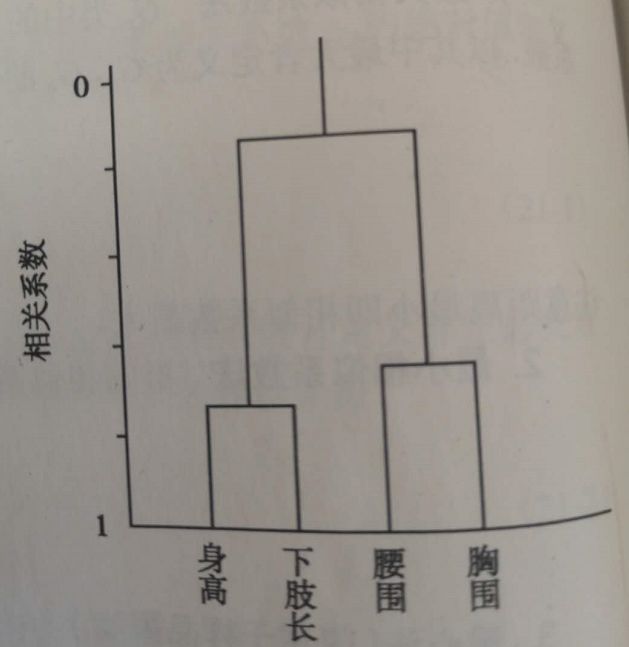
聚类图:
横坐标为指标
纵坐标为相关系数(越往下,r越大)
参考:http://bluewhale.cc/2016-04-19/hierarchical-clustering.html
《 医学统计学》 孙振球,徐勇勇