关于编译原理最小化的操作,专业术语请移步至:http://www.360doc.com/content/18/0601/21/11962419_758841916.shtml
这里只是记录一下个人的理解,以备复习使用
DFA最小化的操作步骤:
1.将DFA未最小化前的状态划分为:终态和非终态
终态就是包含了NFA终点结点的状态集合,如下图的NFA,状态10为NFA的终点,所以在DFA的状态集合中,包含了10这个状态的集合就是DFA的终态,那么,不包含的就是非终态了
值得一提的是,在DFA划分非终态和终态时,有可能得到的非终态是空集(仔细想想,此时意味着所有的DFA的状态集合都包含了NFA的终点(如下图的10)),反之,终态不可能为空集,因为NFA的终点一定会包含在某个DFA的状态集合中。
子集构造的过程如下:(关于子集构造的描述也可以移步至:http://www.360doc.com/content/18/0601/21/11962419_758841916.shtml)
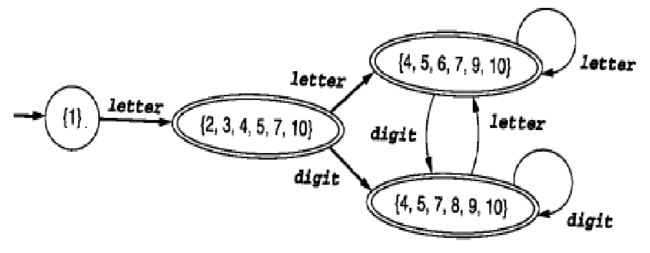
得到的DFA图如下:(双重圈表示终态,单层表示非终态,对照上面所说的,是不是包含了10的都是被归类为终态集合?)
但是,上面划分的终态和非终态只是一个初步的划分,可能在终态(或者非终态)集合内还可以继续划分出多个状态集合
首先看定义:
在DFA中,两个状态等价的条件是:
一致性条件:状态s和t必须同时为终态或者非终态 (什么意思?就是意味着终态和非终态里的状态集合不可能再被划分为相同的状态了,所以第一步划分终态和非终态可以理解为粗略的划分)
蔓延性条件:对于所有输入符号,状态s和状态t必须转换到等价的状态里 。(这该怎么理解呢?请看第二个表)
比如我想知道第二个表中的状态集合[2,3,4,5,7,10]和状态集合[6,9,4,7,10,5] (也即是第二第三行的初始状态集合)是不是属于同一个状态,这个蔓延性条件就是说[2,3,4,5,7,10]经过letter和digit转换得到的[6,9,4,7,10,5] 和 [8,9,4,7,5,10] 与 [6,9,4,7,10,5]经过letter和digit转换得到的[6,9,4,7,10,5] 和 [8,9,4,7,5,10] 是不是同属于同一个状态。(此时可以看出它们都属于终态)。
emmm,感觉我自己表述不清,自己多看书和上面给出的那个连接,应该不难理解的。
接下来说一下我自己划分状态集合的操作。
首先划分成终态和非终态,然后继续在终态和非终态的内部看每个状态之间是否属于同一个状态………………
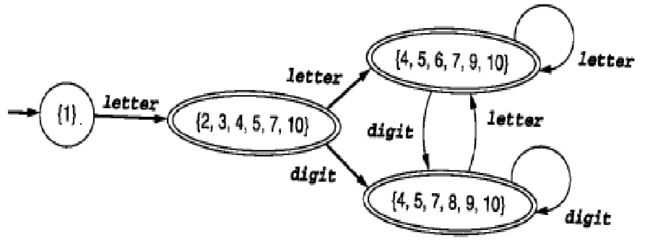
还是以此图为例:
在图中可以看出终态集合为list = [ [2,3,4,5,7,10],[4,5,6,7,9,10],[4,5,7,8,9,10]] 一共三个集合,要继续看这三个集合是否可以进一步细划
我的想法是递归操作,首先将上面的状态集合的第一个子集取出来,并找出其相应的状态(放入一个state1的List中),接着遍历其他的子集,看是否和state1中的集合的状态相同,是的话就放进state1这个List中,不是的话就放进state2这个状态集合中。最后遍历结束的结果是将[ [2,3,4,5,7,10],[4,5,6,7,9,10],[4,5,7,8,9,10]]这个集合划分成两类,第一类state1是与第一个集合list[0] 状态相同的 ,第二类state2是与第一个集合list[0] 状态相不同的。
接下来,可以判断state2是不是空,如果是空的话,就意味着list中的所有子集的状态都是相同的,即state1,如果state2长度为1,也不用继续判断了,直接将list划分为state1和state2两类了。
如果,state2的长度大于1,那么就得继续对state2进行划分,操作步骤和上面划分list的一致,因此可以使用递归操作。
对于非终态,如果需要划分,操作和上面的一样,最后递归划分结束后,得到的是dfa所有的状态。
当然,这只是初步的想法,不知道可不可以,我觉上述想法的难点可能在,当状态划分越来越多的时候,判断两个状态是否属于同一个状态的工作可能会越来越麻烦?