NBER：大流行中个体与集体的权衡 | 唧唧堂论文解析

picture from Internet

解析作者 | 唧唧堂经济金融学写作小组： 维垣 审校编辑 | 悠悠

专栏介绍

长按二维码直接进入专栏

本文为唧唧堂《新冠病毒主题论文导读专栏》内一篇论文解析，唧唧堂将在本专栏收录发布所有新冠病毒主题的经济金融社会心理等社科类论文解析导读，同时也或将收录部分医学论文。

本专栏论文收录无截止时限，现已有超100篇NBER工作论文解析中，未来唧唧堂将源源不断把发现的新冠病毒主题论文放入本专栏，期待各位研究人的关注与订阅。点击了解专栏！

唧唧堂现招募更多经济金融研究人加入写作小组，以更快完成本专栏内容的解析产出，解析作者在获得固定稿费同时，还将获得付费阅读收入的部分提成。点击加入写作小组！

本文是针对工作论文《Optimal Mitigation Policies in a Pandemic: Social Distancing and Working from Home（大流行中个体与集体的权衡）》的一篇解析（NBER Working Paper 26984）。该论文作者是Callum J. Jones, Thomas Philippon, 和Venky Venkateswaran。

研究背景与问题

疫情大流行（Pandemic）势必会造成经济损失。从宏观的角度讲，无论是患病本身还是相应的隔离措施都会导致生产力和消费的下降。今年的COVID-19大流行中，个体行为和政府政策产生冲突的案例比比皆是。例如，春假期间的佛罗里达正好遇上疫情蔓延到美国，尽管政府一直呼吁民众保持社交疏离，却始终有许多人悠哉游哉地聚集在海滩上享受他们地假期。本论文基于传统经济学宏观分析中的新古典增长模型，增加了传染病模型作为经济冲击。作者们通过分别考虑个人的优化问题和社会的优化问题，说明两者最优隔离行为路径的巨大差异，从而尝试解释大流行中个体与集体决策的冲突。一言以蔽之，作者们认为这一冲突主要来自于隔离、染病和医疗资源的外部性。

模型

与同类论文一样，此论文的模型由价值函数和传染病动态两部分构成。为了构建价值函数，此论文采用了Lucas-Stokey的“购物者-生产者”新古典增长模型，并且采用传统的解宏观均衡的方法来解最优隔离路径；传染病动态则使用稍加修改的传染病模型以表现出隔离、染病和医疗资源拥挤的外部性。由于此模型中上述两部分交织在一起，分部门构建也许会使整幅画面更加清晰。

1、家庭

假设经济体中的全部家庭是一个大小为N的连续统，且拥有相同的效用函数如下（假设时间是离散的，折现率为β）

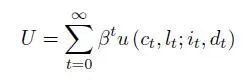
其中c_t是平均每个人的消费，l_t是每个健康人供给的劳动力。从t=0时刻起，每个家庭都有连续统大小都是1；t>0时，s_t, i_t, d_t分别表示某个家庭中易感人群、患病人群和死亡人群的比例（因此每时刻t，家庭的大小都是1-d_t；某个家庭的总消费为c_t(1-d_t)）。在比例为i_t的患病者中，κi_t是病重以至于不能工作的。因此t时刻每个家庭的劳动力数量1-d_t-κi_t，而该时刻每个家庭的劳动力供给为l_t (1-d_t-κi_t)。最后，令r_t = 1 – s_t-i_t-d_t 为康复人群的比例。

此模型的使用的效用函数u(c_t, l_t; i_t, d_t)的形式如下

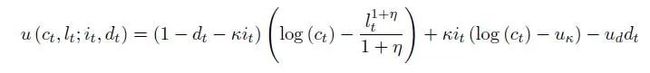
第一项可以看成是t时刻某个家庭中还剩下的能工作的人的总效用，作为可以获得“完整”效用的人数比例近似；第二项表示患病且症状严重的人的效用，其中u_k是患病的负效用；第三项为死者的效用，其中u_d是死亡的负效用。假设患病不影响消费的效用。在每个时间点t，每个家庭决定t时的消费c_t和健康人劳动力供应量l_t。然而，人们知道他们会在购物或工作时增加感染风险，因此我们分别定义购物者和生产者的疫情暴露，之后将他们加总作为人群整体的疫情暴露。

2、购物者

定义“消费暴露”为

其中e^c是一个衡量消费暴露敏感度的系数，C_t是总消费。这个值的单位是一个标准化为1的稳态暴露值。这个表达式说明消费者的暴露程度不仅与他自己选择的消费量正相关，还与人群的总消费量正相关。也就是说，每个人的消费对于社会中的其他人是有外部性的。

3、生产者

假设生产要素只有劳动力。每个家庭的有效生产力供给

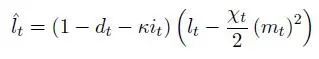
第一项表示每个家庭剩余的有效劳动力的数量，第二项表示采取隔离措施后的单位劳动力供应（主要反映在后面带有χ的那项上面）。本文主要考虑居家办公，并且假设居家办公有个适应性过程（即一开始效率会很低，随着“隔离总量”的增加，效率逐渐提高），因此定义χ_t为一个与“隔离总量”的变化负相关（实际解模型时假设其为凸函数）的熟练度系数。其中隔离总量被正式定义如下

m_t是t时刻的隔离强度（可理解为t时刻在家工作的占比，m_t=1则说明t时刻的工作全部在家完成），不难看出，隔离总量是直到t时刻所有隔离量m的累计。

我们可以进而定义“工作暴露”如下

与消费暴露类似，e^l是工作暴露敏感度系数，m是某个家庭的隔离行为，而M是整个社会的隔离行为，L为整个社会的劳动力总供给。工作暴露定义的逻辑和消费暴露是类似的，只是加上了隔离系数1-m或1-M。

除此之外，整个模型资源约束为:

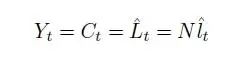
假设公司同质化和完美竞争，则价格等于边际成本

其中W为单位劳动力的工资，标准化为1。

4、收入与暴露加和

假设每个t时期末，每个家庭会分享收入和消费。因此他们有消费/存款约束如下（注：此处的r_t或应该为折现率，文中的字母用的是β）

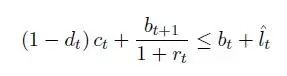
而一个家庭的总疫情暴露（购物者与生产者的加和）为

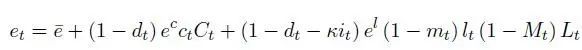
其中e_bar是一个独立于隔离行为的基线暴露值（常数），而后面两项很明显是由消费暴露和工作暴露按人数加和而成。

5、传染病动态模型

本文的传染病动态模型由以下微分方程组所表征

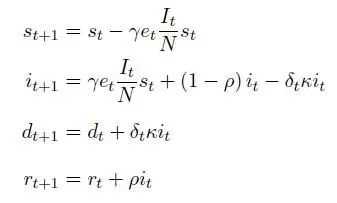
显然，这四行方程分别代表易感人群s、患病人群i、死亡人群d和康复人群r的变化情况。γ是每一时间染病的概率（换言之，染病是一个泊松率为γ的随机过程，下文其他量的定义也类似）；ρ是康复率；κ是感染后得重病（以至于无法工作）的概率（也就是说这个模型其实模拟了存在“无症状感染者”的情形）；而得重病的人每一时刻有δ的概率会死亡。在传统的SIR模型中δ是外生的，但此处δ随着社会中患者(I)比例的增加而变大，以模拟医疗资源饱和的情形。

均衡

个体优化均衡

个体优化即以家庭为单位优化，解出最优总体均衡。首先按照传统步骤写出家庭的价值函数：

家庭个体通过选择每一时刻的消费、劳动力供给和隔离程度来最大化这个价值函数。其中t时刻的状态e_t, s_t, i_t, d_t, 和l_t分别由上文模型中的动态变化约束，故可推导出其拉格朗日方程为：

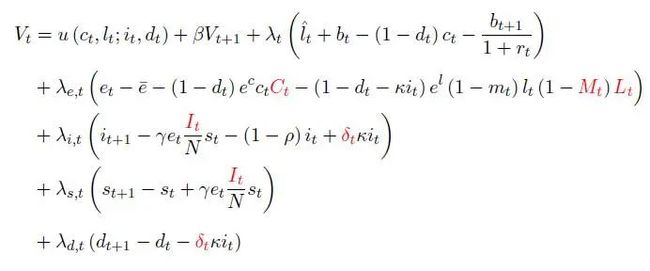
显然，红色高亮部分为外部性在模型中的体现。求出一阶导数条件如下