从C、DS、计组一路折磨过来, 几乎都在采用过程化、函数式的编程思想。初接触面向对象的项目开发,经过了三周的对多项式求导问题的迭代开发,经历了设计、coding、测评环节,算是对面向对象有了一定的认识,这个过程总结了一些经验,在这里希望和大家一起share,欢迎大家给我提意见。
一、关于代码架构
1、第一次作业
主要设置了3个class
PolyComputer作为主类,进行I/O操作,正则表达式匹配,项的提取,合并同类型,排序这些操作
PolyTerm表示每一项,包含项的基本特征系数和指数,constructor(处理每个String项,提取系数和幂),以及获取和修改系数和指数,转化为String这些Methods.
PolyDerivation继承PolyTerm,修改构造器,继承PolyTerm的Methods.
整体思路分析:
1、在PolyComputer类中,使用正则表达式匹配每一项,并提取项之间的符号。(一项一项匹配可以有效防止爆栈问题,当然还可以使用独占模式进行匹配来避免,我会在后面的作业
使用到,这里推荐一个学习链接https://blog.csdn.net/weixin_42516949/article/details/80858913)
2、在PolyComputer类中,把提取出的符号和项进行合并,由于这里存在正负性的问题,我是单独设置了一个Method去合并,其实在提取过程中边提取边合并也不失为一种好方法
(个人甚至更推崇)。
3、提取出的每一个String类的terms传给PolyDerivation(继承PolyTerm)的生成器,在super(term)中采用正则表达式提取系数和指数,然后根据求导法则,进行求导。
4、合并同类项、排序(可有可无,可以考虑在排序过程中增加一种量化方法即尽量选取正数项为开头,提升性能)、输出
2、第二次作业
第二次作业的整体架构跟第一次比没有太大的变化,主要就是修改了提取各个项的方法(引入了由乘号连接因子的项的情况,需要修改正则表达式,而在这里为了保险起见,避免爆栈
我采用了独占模式的正则表达式匹配),对于每个项,由于都可以抽象为(x_coeff,x_deg,sin_deg,cos_deg)的形式,因此在PolyTerm类中增加了对sin,cos的指数的提取,修改
PolyDerivation的生成器,在继承PolyTerm的基础上转化为更复杂的链式求导法则。
反思:
1、应该增设factor类,求导方法类,使架构更OO,也便于后续开发。
2、优化只停留在合并同类项和对sin(x)^2+cos(x)^2=1的简单优化(二次项优化),目前打算修改为启发式化简(在讨论课上已经详细介绍过,也是python的sympy库的优化方法)的方法,提升性能。
3、第三次作业
从类图可以看出来,这很不OO,这是一次比较难受的迭代开发,我主要增设了求导方法和求导(递归)两个类,主类的方法也进行了大量的修改(主要体现在开头就进行了
非法字符的识别,去空白符等操作,把原先留给后面的提取和求导的复杂度提前,为相对这次比较复杂的递归求导开辟一条相对平坦的路,提高求导过程的开发体验)
本次的架构还有大量需要改进的地方,这里并不推荐,将主要阐述我所采用的递归求导方法。
我没有采用主流的递归下降的词法分析方法。
而是采用了层层拆解的方法
1、拆项(split)
所有的expression都可以以+/-为分隔拆解成为term,运用加法求导法则
term = split(str,1); if (term.size() > 1) { return method.plusRules(term); }
所有的term都可以以*为分隔拆解为factor,运用乘法求导法则
term = split(str,2);
于是,我创造了
public String plusRules(ArrayListterm) {} public String multRules(ArrayList term, int i,String strIn) {} public ArrayList split(String str, int mode) {}
这里需要用到栈(java自带栈,教程请移步https://www.jb51.net/article/130374.htm)其用于括号匹配,保证split的正确性,是个非常好用的手段。
2、对于不可拆项的预处理
去括号
由于多层嵌套以及表达式因子的存在,为了后续求导的便捷我单独写了一个去括号的Method,做一个化简
public String strip(String strIn) {
Stack stack = new Stack<>();
....
}
3、对于不可拆项的求导
主要分成三类
(1)满足第二次作业可求导的部分
public String matchBasic(String str) {} public String multForBasic(ArrayListterm, int i) {}
(2)带幂次方的部分
public String matchPower(String str) {} public String multForPowerRules(ArrayListterm, int i) {}
(3)带sin、cos的嵌套因子
public int matchTrig(String str,int mode) {} public String multForSin(ArrayListterm, int i) {} public String multForCos(ArrayList term, int i) {}
于是,在类DerivationMethod 和 Derivation中部署好相应的Method之后,递归的框架也形成了
//...... while (!str.equals(strip(str))) { str = strip(str); } //...... term = split(str,1); if (term.size() > 1) { return method.plusRules(term); } //...... term = split(str,2); //...... for (i = 0; i < term.size(); i++) { if (!matchPower(term.get(i)).equals("")) { returnString = returnString + method.multForPowerRules(term,i); } else if (matchTrig(term.get(i),1) != -1) { returnString = returnString + method.multForSin(term,i); } else if (matchTrig(term.get(i),2) != -1) { returnString = returnString + method.multForCos(term,i); } else if (!matchBasic(term.get(i)).equals("") || term.size() > 1) { returnString = returnString + method.multForBasic(term,i); } else { //WF } } return returnString;
这就是我搭建的递归框架,不得不感叹函数式编程深入人心,也希望大家能对我的方法提出宝贵的意见
二、自我BUG总结
三次测评,公测中共被hack一次,互测共被发现两个bug
第一次公测中被发现的bug出现在类PoltTerm的toString()法中,是典型的手抖党bug。
else if (this.coeff.equals(new BigInteger("-1"))) { output = '-' + "*x^" + String.valueOf(this.deg);
看了这段代码不禁惊叹-*x是什么鬼????这是什么神仙bug,显然这个bug非常之好改,删除*就完事了
第一次互测中除了被人发现了上述的bug,万万没想到还有一个惊天的bug
某匿名朋友向我扔了一个1+,然后我死了
后来我发现,这个方法来自于我的提取项和符号的过程,一项一项匹配的方法有一个致命的需要判断的地方,就是提取出的项数和符号数万万不能相等,于是我做出了这样的修改
if (terms.size() == ops.size()) { System.out.println("WRONG FORMAT!"); System.exit(0); }
第一次作业以被hack的面目全非告终了
第二次,
我总结了第一次作业的教训,比如尝试构造覆盖性样例,没有自动化的疯狂测试,没有做单元模块测试
于是,装备上了自动化评测机、翻看了无数遍指导书、做了分块测试后的第二次公测、互测我终于完好无缺得活着了
第三次,事情又有那么一些不简单
这一次的错误来源于我对指导书的理解的偏差
指导书中有这么一句话",例如1926^0817是不合法的,因为幂函数的自变量只能为x。",于是我天真的以为类似于
sin(sin(sin((-+3+-8*-1))^9))^47的样例是绝对不合法的,因此他们没有自变量x,于是我在互测中果然被hack了。
但是其实这个幂是在三角函数上的。指导书理解偏差的惨痛经历。
反思
从我自己课下debug的过程以及测试中被发现的bug来看,设计结构跟debug的难易程度以及bug的数量是息息相关的。
***第一次的bug除了测试方法的锅,还有一个重要原因就是Method的长度,设计中设计了比较长的Method(现在看来30行左右的体验是最好的)容易导致逻辑错误,思维混乱,然后就手抖了
***自己测试过程(尤其是第三次),由于一些重要的类,例如Dervation类过长,递归过程中的异常情况经常出现,并且难以定位。而且Derivation中的split方法也比较长,较多的if-else
严重影响了自己的体验。
***类的拆分很重要,前两次我都直接定义了Term类,而忽略了Factor类,导致了Term类复杂度过高(尤其是正则表达式)出错的情况不在少数。
***对WF做单独检查真的太重要!!!!!!为了有效防范过程中重复不断的WF,写一个Method或者甚至Class来检查格式会让设计过程中集中精力在功能,体验更佳。
三、测试方法分析
这三次多项式求导是第一次对WF有了这么深的认识,也是第一次进行如此高强度的测试(尤其是互测和强测环节)。从第一次在强测环节遭到hack后的思考总结,以及讨论区的各个帖子,逐渐摸索出一些比较有效的测试方法。
先从傻瓜测试讲起:第一次测试,没有进行模块化的功能测试,自己构造的样例测试不全面,想到什么样例测什么,一切都有点糟糕。(让我第一次公测崩掉一个case的罪魁祸首!!
后来,事情终于逐渐有了转机。
Method1: 模块化测试
对设计的每个class,每个method,在设计过程中,完成每一部分后进行测试,尤其是分支语句各个部分 都要有样例覆盖(第一次在这里吃大亏了!!)。
Method2: out of bounds检查
众所周知,设计过程中难免使用到charAt,substring等语句,极容易碰到OUT OF BOUNDS的报错(尤其 是一不小心字符串被化简成空串的情况!!),为了有效规避这类常见错误,个人采取了设计之后搜索charAt ,sustring等关键字,逐条检查。
Method3: 无比快乐的自动化测试
这里采用我比较熟悉的python。
1、随机生成测试case
Xeger
Library to generate random strings from regular expressions
在写自动化测试的case的时候,采用Xger库根据正则表达式随机生成测试数据,测试效率将会大大提高
(java也可以使用Xeger,进行随机生成,具体见buaa_oo讨论区大佬的分享)
to install,type: pip install xeger to use,type:
from xeger import Xeger x = Xeger(limit=const) #const can be changed x.xeger("your regular expression")
注:
*前两次作业可以直接复用java中的正则表达式,设置好limit(可以采用random库生成),直接生成case
def creat_factor(): def creat_term(): #creat_factor() * creat_factor() def creat_expr(): #creat_term() +creat_term()
*第三次作业加入嵌套因子和表达式因子之后,在creat_factor()中做微调引入creat_expr() 以及增加random函数设置嵌套层数。
*关于WF的测试:random函数对生成的结果做随机删除
2、打包程序,I/O操作
os库
os 模块提供了非常丰富的方法用来处理文件和目录。这里我们借助os指导python进行文件路径的访问。
subprocess
subprocess包中定义有数个创建子进程的函数,这些函数分别以不同的方式创建子进程,所以我们可以根据需要来从中选取一个使用。另外subprocess还提供了一些管理标准流(standard stream)和管道(pipe)的工具,从而在进程间使用文本通信。在这里我们借助subprocess讲信息输入给java,获取java输出。
to use,type: import os import subprocess def get_output(path,java_main,input): os.chdir(path) #改变工作目录到java文件的目录 #class Popen(args, bufsize=0, executable=None, stdin=None, #stdout=None, stderr=None, preexec_fn=None, #close_fds=False, #shell=False, cwd=None, env=None, universal_newlines=False, #startupinfo=None, creationflags=0) out, err = popen.communicate(input=bytes(input.encode('utf-8'))) #get stdout, stderr os.chdir('..') #返回上级目录 return str(out.decode())
注:
*调用cmd对.java进行编译
to use,type: cd java_src javac *.java cd ..
3、合法性验证
由于不太会用python比对运行结果,因此我采用了更加简便的matlab进行结果比对
(也可以给python引入malb库,但是博主在安装过程中碰到了严重的编码问题(可能还是比较菜),因此还在尝试,稍后成功后会作出补充)
利用python把输入,输出存到文件中,利用matlab读取文件,把输入用matlab求导后,与输出做比对(这里我采用了给x赋 [-100,100]区间内的值,比对计算结果的方法)。
to use,type:
syms x
%fopen() while feof(fp)~=1 %fgetl() %diff() for i = -100:100: %compare
4、多看指导书!!!手动搭样例!!!!
个人认为,自动化测试几乎可以覆盖性得测试,但是为了防止指导书理解偏差等带来的bug,还是多看几遍指导书,动手再搭一些样例(尤其是指导书的特殊情况)比较稳妥。
四、互测策略
互测策略主要和上述自己的测试方法接近
主要进行黑盒测试:
1、记录自己的存在bug的样例,便于后续用来hack别人(亲测相当有效
我会把所有的样例存在txt文件中,后续直接在文件中调出,输入程序
就像这样:
2、打包
既然进行黑盒测试,不如打包好,用python直接输入、输出,方法与上述自动化测试方法中一样,是提高效率的重要方法
3、评测机疯狂测试
用自己已经搭建好的评测机,疯狂自动化测试,个人经验基本上可以覆盖掉所有bug,体验极佳
辅助白盒测试:
我会选择性调用几份代码学习顺便找bug,着重关注if-else语句逻辑,正则表达式的正确性(对发现WF极有帮助),输出逻辑等
五、基于度量的关于架构的深刻反思和重构思路
这三次作业(尤其是最后一次)的代码结构是我本次算是最不满意的地方
因此,我选择单独开一个部分对本次架构做深刻的反思。
对三次的代码的class和method分别做了复杂度分析
第一次作业:
主类和Term类设计存在问题
主类PolyComputer的frontDeal、getTermsAndOps的ev(G)偏高
frontDeal和getTermsAndOps中都对WF的情况过量判断,好的架构应该倾向于单独的Method中做统一判断,或者使用简介的 正则表达式一次判断。
PolyTerm类中存在的问题主要集中在toString(),其中过多的if-else给代码维护带来了极大额困难,应该重新设计一个Method做简化输出的工作,便于维 护。
第二次作业:
除了和第一次有类似的问题之外(其中简化过程的问题与第一次的问题不谋而合),类的设计的问题更为突出。直接跳到Term类,而不设置Factor类, 无疑不适合当下已经比较复杂的表达式了,正则表达式过长,Term类承担过重负担,没有设置单独求导接口带来的代码复杂度高、极其不容易维护以
及复用性差等问题凸显。
一个好的架构应该更倾向于求导方法的接口化、甚至设置单独求导类或方法(因为求导法则只会越来越多越来越复杂,应该考虑后续不断增加的需求)
设置有层次的Factor和Term,并采用继承和多态来组织。
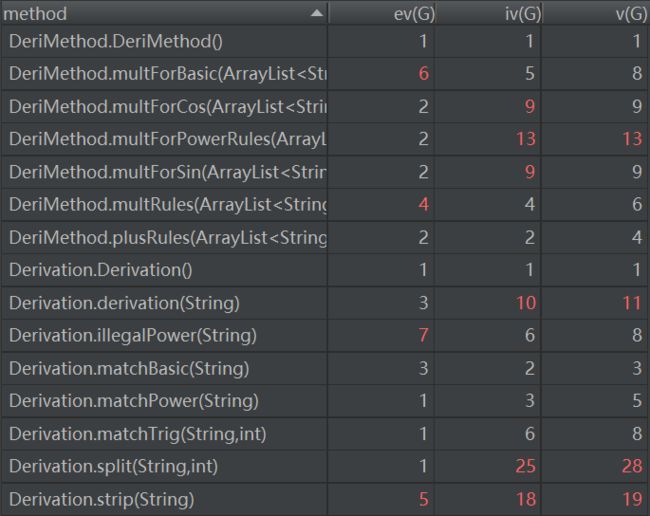
第三次作业:
我对第三次的构造方法只是采取了对第二次简单的沿用封装和新的求导规则的重新构建(因为前面架构实在不适合第三次了),新的Derivation和 DerivationMethod的构造问题
这么多飘红,惊了
可见这次的无论是递归求导还是求导方法的构建都是比较失败的
(1)本次更凸显Factor的重要地位,以及各种Fator、Term间千奇百怪的求导规则,嵌套因子和表达式因子的新加入就更需要Factor来承担起家庭的重任,而我寻求的层层拆解最后抽象成三类的求导准则无疑太复杂了,大概也撑不起下一次的迭代开发了,有牵一发而动全身的风险。应该采用层层拆解后把部分任务分担给各种小类来减轻Derivation的工作压力。
(2)设置求导方法接口已经刻不容缓。expr-factor,term-term,factor-factor各种间作用的求导方法和接口值得被开发。