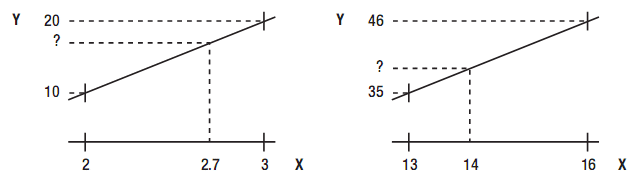图像直方图与直方图均衡化
图像直方图与直方图均衡化
图像直方图以及灰度与彩色图像的直方图均衡化
图像直方图:
概述:
图像的直方图用来表征该图像像素值的分布情况。用一定数目的小区间(bin)来指定表征像素值的范围,每个小区间会得到落入该小区间表示范围的像素数目。
图像直方图图形化显示不同的像素值在不同的强度值上的出现频率,对于灰度图像来说强度范围为[0~255]之间,对于RGB的彩色图像可以独立显示三种颜色的图像直方图。
同时直方图是用来寻找灰度图像二值化阈值常用而且是有效的手段之一,如果一幅灰度图像的直方图显示为两个波峰,则二值化阈值应该是这两个波峰之间的某个灰度值。
并且直方图是调整图像对比度的重要依据,直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。
下面我将介绍如何用python绘制图像直方图,以及直方图均衡化的原理并给出灰度图与彩色图的直方图均衡化。
使用python绘制图像直方图:
在之前写的《python基本图像操作》中已经提到了如何用python去绘制图像的直方图,python的优点就是具有众多扩展库和更加易用,所以可以避免陷入算法细节从更宏观的角度实现自己的想法,所以用python绘制直方图非常简单:
使用Matplotlib绘制直方图
(灰度)图像的直方图可以使用 hist() 函数绘制:
hist() 函数的第二个参数指定小区间的数目。需要注意的是,因为 hist() 只接受一维数组作为输入,所以我们在绘制图像直方图之前,必须先对图像进行压平处理。flatten() 方法将任意数组按照行优先准则转换成一维数组。
# -*- coding: utf-8 -*-
from PIL import Image
from pylab import *
# 读取图像到数组中,并灰度化
im = array(Image.open('./source/test.jpg').convert('L'))
# 直方图图像
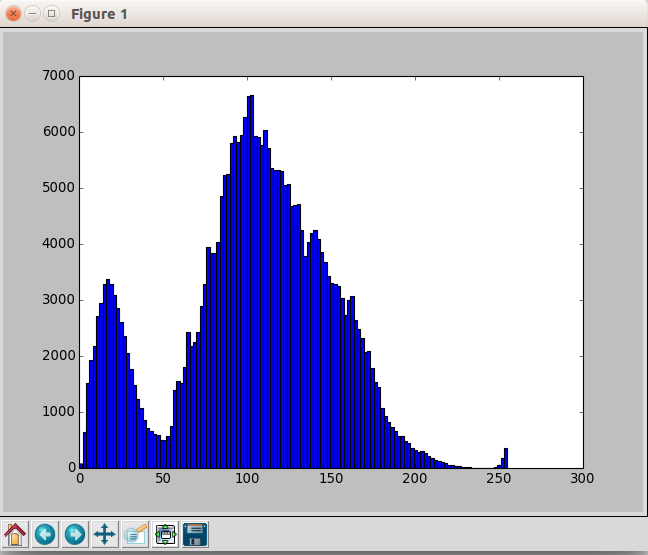
hist(im.flatten(),128)
# 显示
show()测试图片
Test.jpg
运行结果
直方图的原理也很简单了,自己实现也非常简单,所以也没有必要再过多叙述,具体细节可以去看一下C++的实现。
直方图均衡化(Histogram Equalization):
概述:
直方图均衡化是非常有用的一种变换,直方图均衡化是指将一幅图像的灰度直方图变平,使变换后的图像中每个灰度值的分布概率都相同。在对图
像做进一步处理之前,直方图均衡化通常是对图像灰度值进行归一化的一个非常好的方法,并且可以增强图像的对比度。
如果一副图像的像素占有很多的灰度级而且分布均匀,那么这样的图像往往有高对比度和多变的灰度色调。直方图均衡化就是一种能仅靠输入图像直方图信息自动达到这种效果的变换函数。它的基本思想是对图像中像素个数多的灰度级进行展宽,而对图像中像素个数少的灰度进行压缩,从而扩展像原取值的动态范围,提高了对比度和灰度色调的变化,使图像更加清晰。
图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。直方图拉伸是通过对比度拉伸对直方图进行调整,从而“扩大”前景和背景灰度的差别,以达到增强对比度的目的,这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。
直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。这种方法通常用来增加许多图像的局部对比度,尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法,亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度,直方图均衡化通过有效地扩展常用的亮度来实现这种功能。
这种方法对于背景和前景都太亮或者太暗的图像非常有用,这种方法尤其是可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。这种方法的一个主要优势是它是一个相当直观的技术并且是可逆操作,如果已知均衡化函数,那么就可以恢复原始的直方图,并且计算量也不大。
这种方法的一个缺点是它对处理的数据不加选择,它可能会增加背景杂讯的对比度并且降低有用信号的对比度;变换后图像的灰度级减少,某些细节消失;某些图像,如直方图有高峰,经处理后对比度不自然的过分增强。
实现:
直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。
直方图均衡化的基本思想是把原始图的直方图变换为均匀分布的形式,这样就增加了象素灰度值的动态范围从而可达到增强图像整体对比度的效果。设原始图像在(x,y)处的灰度为f,而改变后的图像为g,则对图像增强的方法可表述为将在(x,y)处的灰度f映射为g。在灰度直方图均衡化处理中对图像的映射函数可定义为:g = EQ (f),这个映射函数EQ(f)必须满足两个条件(其中L为图像的灰度级数):
(1)EQ(f)在0≤f≤L-1范围内是一个单值单增函数。这是为了保证增强处理没有打乱原始图像的灰度排列次序,原图各灰度级在变换后仍保持从黑到白(或从白到黑)的排列。
(2)对于0≤f≤L-1有0≤g≤L-1,这个条件保证了变换前后灰度值动态范围的一致性。
累积分布函数(cumulative distribution function,CDF)即可以满足上述两个条件,并且通过该函数可以完成将原图像f的分布转换成g的均匀分布。此时的直方图均衡化映射函数为:
累计分布函数(CDF)就是是概率密度函数(probability density function/pdf)的积分,相信学过概率论的同学对他一定不陌生:
累积分布函数(cumulative distribution function)定义 对连续函数,所有小于等于a的值,其出现概率的和。F(a)=P(x<=a)
所以总结一下灰度图直方图均衡化算法的步骤就是:
- (1) 根据输入的灰度图像计算其原始直方图
- (2) 对输入的原始直方图进行累加,计算其cdf
- (3) 使用累计分布函数的插值计算新的灰度值(这里我使用比较常用的线性插值)
使用python及其数学库的话求直方图和cdf的方法已经为我们封装好了,所以实现起来代码量是很少的:
# -*- coding: utf-8 -*-
from PIL import Image
from pylab import *
#读取图像到数组中,并灰度化
im = array(Image.open('./source/test.jpg').convert('L'))
#绘制原始直方图
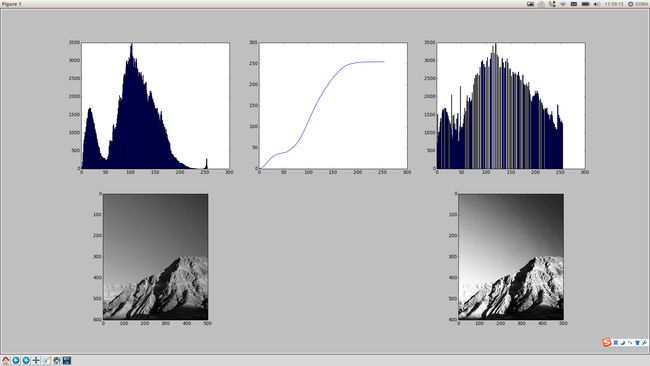
subplot(231)
hist(im.flatten(),256)
#计算图像直方图(每个bins数组的区间值对应一个imhist数组中的强度值)
imhist,bins = histogram(im.flatten(),256,normed=True)
#计算累积分布函数
cdf = imhist.cumsum()
#累计函数归一化(由0~1变换至0~255)
cdf = cdf*255/cdf[-1]
#绘制累计分布函数
subplot(232)
plot(bins[:256],cdf)
#依次对每一个灰度图像素值(强度值)使用cdf进行线性插值,计算其新的强度值
#interp(x,xp,yp) 输入原函数的一系列点(xp,yp),使用线性插值方法模拟函数并计算f(x)
im2 = interp(im.flatten(),bins[:256],cdf)
#将压平的图像数组重新变成二维数组
im2 = im2.reshape(im.shape)
# 显示均衡化之后的直方图图像
subplot(233)
hist(im2.flatten(),256)
#显示原始图像
gray()
subplot(234)
imshow(im)
#显示变换后图像
subplot(236)
imshow(im2)
show()运行结果
其中线性插值公式是最常用、最简单的插值公式。线性插值和双线性插值是图形学中常用的技术,旋转变换后图片会有一些不连续点,就是通过双线性插值法解决的,之后我会单独写一篇博客进行详细介绍,这里简单介绍一下线性插值的原理:
处理分离的数据,如果想知道分离点之间的某些值,需要用到某种类型的插值。
使用线性插值,通过连接两点的线段找到X=2.7对应的Y值
0.7* (maxY-min Y)+minY=0.7*(20-10)+10=0.7*10+10=17
(14-minX)/(maxX-minX) =(14-13)/(16-13)=0.33
0.33* (maxY-minY)+minY=0.33*(46-35)+35=0.33*11+35=3.67+35=38.67
顺便说一下,基本所有的线性插值返回的都是浮点数。
所以我们使用插值技术利用离散的cdf得出新的灰度强度值。
彩色图像的直方图均衡化(Histogram Equalization):
一幅彩色图像由RGB三色通道构成,每个通道都是描述了该种颜色的强度(0-255)的一幅灰度图,所以比较简单的应用于彩色图像的均衡化就是把每个颜色通道均衡化之后进行合成,下面是我的具体实现:
# -*- coding: utf-8 -*-
from PIL import Image
from pylab import *
import copy
# 读取图像到数组中
im = array(Image.open('./source/test.jpg'))
#获取通道
r = im[:,:,0]
g = im[:,:,1]
b = im[:,:,2]
#显示各个通道原始直方图,均值化之后的直方图以及累计分布函数
figure()
#计算各通道直方图
imhist_r,bins_r = histogram(r,256,normed=True)
imhist_g,bins_g = histogram(g,256,normed=True)
imhist_b,bins_b = histogram(b,256,normed=True)
subplot(331)
hist(r.flatten(),256)
subplot(332)
hist(g.flatten(),256)
subplot(333)
hist(b.flatten(),256)
#各通道累积分布函数
cdf_r = imhist_r.cumsum()
cdf_g = imhist_g.cumsum()
cdf_b = imhist_b.cumsum()
#累计函数归一化(由0~1变换至0~255)
cdf_r = cdf_r*255/cdf_r[-1]
cdf_g = cdf_g*255/cdf_g[-1]
cdf_b = cdf_b*255/cdf_b[-1]
#绘制累计分布函数
subplot(334)
plot(bins_r[:256],cdf_r)
subplot(335)
plot(bins_g[:256],cdf_g)
subplot(336)
plot(bins_b[:256],cdf_b)
#绘制直方图均衡化之后的直方图
im_r = interp(r.flatten(),bins_r[:256],cdf_r)
im_g = interp(g.flatten(),bins_g[:256],cdf_g)
im_b = interp(b.flatten(),bins_b[:256],cdf_b)
# 显示直方图图像
subplot(337)
hist(im_r,256)
subplot(338)
hist(im_g,256)
subplot(339)
hist(im_b,256)
#显示原始通道图与均衡化之后的通道图
figure()
gray()
#原始通道图
im_r_s = r.reshape([im.shape[0],im.shape[1]])
im_g_s = g.reshape([im.shape[0],im.shape[1]])
im_b_s = b.reshape([im.shape[0],im.shape[1]])
#均衡化之后的通道图
im_r = im_r.reshape([im.shape[0],im.shape[1]])
im_g = im_g.reshape([im.shape[0],im.shape[1]])
im_b = im_b.reshape([im.shape[0],im.shape[1]])
subplot(231)
imshow(im_r_s)
subplot(232)
imshow(im_g_s)
subplot(233)
imshow(im_b_s)
subplot(234)
imshow(im_r)
subplot(235)
imshow(im_g)
subplot(236)
imshow(im_b)
#显示原始图像与均衡化之后的图像
figure()
#均衡化之后的图像
im_p = copy.deepcopy(im)
im_p[:,:,0] = im_r
im_p[:,:,1] = im_g
im_p[:,:,2] = im_b
subplot(121)
imshow(im)
subplot(122)
imshow(im_p)
show()
运行结果
figure1:RGB通道的原始直方图,cdf,均衡化后的直方图 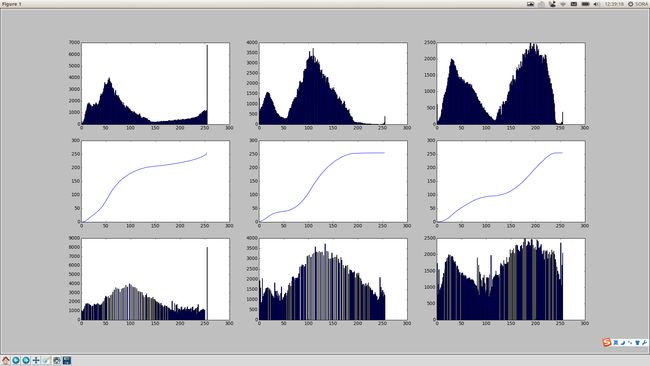
figure3:原始图像,均衡化后的图像
结语:
本篇博客介绍了图像直方图和图像直方图均衡化的原理和方法,希望我的博客对大家有所帮助~