本文主要描述实现LU分解算法过程中遇到的问题及解决方案,并给出了全部源代码。
1. 什么是LU分解?
矩阵的LU分解源于线性方程组的高斯消元过程。对于一个含有N个变量的N个线性方程组,总可以用高斯消去法,把左边的系数矩阵分解为一个单位下三角矩阵和一个上三角矩阵相乘的形式。这样,求解这个线性方程组就转化为求解两个三角矩阵的方程组。具体的算法细节这里不做过多的描述,有很多的教材和资源可以参考。这里推荐的参考读物如下:
Numerical recipes C++,还有包括MIT的线性代数公开课。
2. LU分解有何用?
LU分解来自线性方程组求解,那么它的直接应用就是快速计算下面这样的矩阵乘法
A^(-1)*b,这是线性方程组 Ax=b 的解
3. 分块LU分解算法
如果矩阵很大,采用分块计算能有效减小系统cache miss,这也是很多商业软件的实现方法。分块算法需要根据非分块算法本身重新设计算法流程,而不是简单在代码结构上用分块内存直接去改。线性代数的开源软件有很多,这里我就不枚举了。我主要测试了MATLAB和openCv的实现。MATLAB的矩阵运算的效率是及其高效的,openCv里面调用了著名的LAPACK。大概看了LAPACK的实现,用的也是分块算法。
LU分解的分块算法的文献比较多,我主要参考了下面的两篇文献:
LU分解分快算法的研究与实现
LU分解递归算法的研究
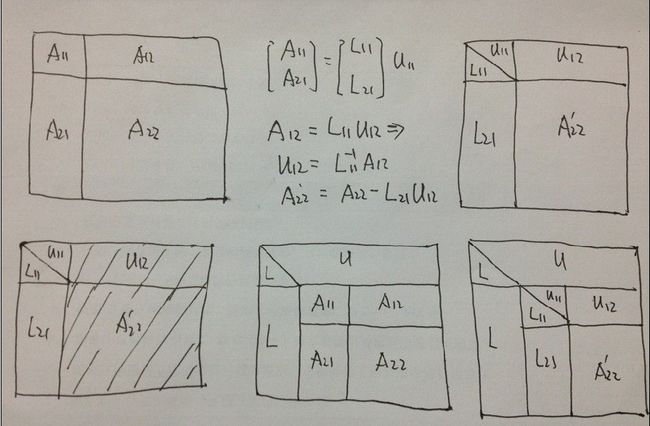
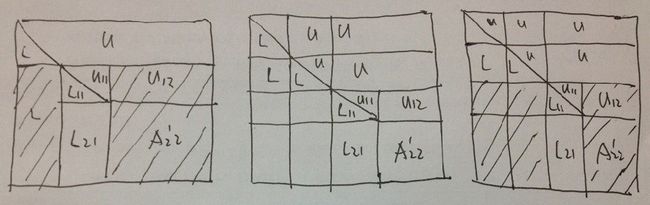
我作了两张图,可以详细的描述算法,这里以应用比较广泛的部分选主元LU块分解算法的执行过程。
图中的画斜线的阴影部分,表示要把当前块LU分解得到的排列矩阵左乘以这部分数据组成的子矩阵,以实现行交换。从上图可以看出,在第一块分解之后,只需要按照排列矩阵交换A12,A22组成的子矩阵,而后面的每一次,则需要交换两个子矩阵。
块LU分解算法主要由4部分构成:
非块的任意瘦型矩阵的LU分解, 行交换,下三角矩阵方程求解, 矩阵乘法.
LU分解来自方阵的三角分解。实际上,任意矩阵都有LU分解。但这里一般需要求解非分块的瘦型矩阵的LU分解,可以采用任意的部分选主元的LU分解算法。但是实现起来仍然有讲究,如果按照LAPACK实现的算法仍然不会快,而采用crout算法实现的结果是很快的。在我的测试中,采用crout算法的1024大小的矩阵非分块的LU分解和LAPACK实现的分块大小为64时的性能相当。LAPACK实现的算法本身是很高效的,但是其代码本身没有做太多的优化。实际上,没有经过任何优化的LAPACK的代码仍然比较慢。
对于行交换,虽然在理论上有个排列矩阵,排列矩阵左乘以矩阵实现行交换,这只是理论上的分析。但实际编程并不能这样做,耗内存,而且大量的零元素存在。一般用一个一维数组存储排列矩阵的非零元素的位置。而原位矩阵多个行交换的快速实现我仍然没有找到有效的方法,我使用了另外一个缓存,这样极其简单。
求解下三角矩阵方程的实现也是有讲究的,主要还是需要改变循环变量的顺序,避免cache miss。
矩阵乘法则是所有线性代数运算的核心。矩阵乘法在LU分块算法中也占据大部分的时间。我会专门写一篇文章来论述本人自己实现的一种独特的方法。
4. 性能指标
经过本人的努力和进一步评估,在单核情况下,LU分解算法的计算时间可以赶上商业软件MATLAB的性能。
5. 实现代码
这里给出分块LU分解的全部代码。
void fast_block_matrix_lu_dec(ivf64* ptr_data, int row, int coln, int stride, iv32u* ipiv, ivf64* ptr_tmp)
{
int i,j;
int min_row_coln = FIV_MIN(row, coln);
iv32u* loc_piv = NULL;
ivf64 timer_1 = 0;
ivf64 timer_2 = 0;
ivf64 timer_3 = 0;
ivf64 timer_4 = 0;
if (row < coln){
return;
}
memset(ipiv, 0, sizeof(iv32u) * row);
if (min_row_coln <= LU_DEC_BLOCK_SIZE){
fast_un_block_matrix_lu_dec(ptr_data, row, coln, stride, ipiv, ptr_tmp);
return;
}
loc_piv = fIv_malloc(sizeof(iv32u) * row);
for (j = 0; j < min_row_coln; j += LU_DEC_BLOCK_SIZE){
ivf64* ptr_A11_data = ptr_data + j * stride + j;
int jb = FIV_MIN(min_row_coln - j, LU_DEC_BLOCK_SIZE);
memset(loc_piv, 0, sizeof(iv32u) * (row - j));
fIv_time_start();
fast_un_block_matrix_lu_dec(ptr_A11_data, row - j, jb,
stride, loc_piv, ptr_tmp);
timer_1 += fIv_time_stop();
for (i = j; i < FIV_MIN(row, j + jb); i++){
ipiv[i] = loc_piv[i - j] + j;
}
if (j > 0){
ivf64* ptr_A0 = ptr_data + j * stride;
fIv_time_start();
swap_matrix_rows(ptr_A0, row - j, j, stride, loc_piv, row - j);
timer_2 += fIv_time_stop();
}
if (j + jb < row){
ivf64* arr_mat_data = ptr_A11_data + LU_DEC_BLOCK_SIZE;
ivf64* ptr_U12 = arr_mat_data;
ivf64* ptr_A22;
ivf64* ptr_L21;
int coln2 = coln - (j + LU_DEC_BLOCK_SIZE);
if (coln2 > 0){
fIv_time_start();
swap_matrix_rows(arr_mat_data, row - j, coln2, stride, loc_piv, row - j);
low_tri_solve(ptr_A11_data, stride, ptr_U12, LU_DEC_BLOCK_SIZE, coln2, stride);
timer_3 += fIv_time_stop();
}
if (j + jb < coln){
ptr_L21 = ptr_A11_data + LU_DEC_BLOCK_SIZE * stride;
ptr_A22 = ptr_L21 + LU_DEC_BLOCK_SIZE;
fIv_time_start();
matrix_sub_matrix_mul(ptr_A22, ptr_L21, row - (j + LU_DEC_BLOCK_SIZE),LU_DEC_BLOCK_SIZE, stride,
ptr_U12, coln - (j + jb));
timer_4 += fIv_time_stop();
}
}
}
fIv_free(loc_piv);
printf("unblock time = %lf\n", timer_2);
printf("swap time = %lf\n", timer_4);
printf("tri solve time = %lf\n", timer_3);
printf("mul time = %lf\n", timer_1);
}void fast_un_block_matrix_lu_dec(ivf64* LU, int m, int n, int stride, iv32s* piv, ivf64* LUcolj)
{
int pivsign;
int i,j,k,p;
ivf64* LUrowi = NULL;
ivf64* ptrTmp1,*ptrTmp2;
ivf64 max_value;
for(i = 0; i <= m - 4; i += 4){
piv[i + 0] = i;
piv[i + 1] = i + 1;
piv[i + 2] = i + 2;
piv[i + 3] = i + 3;
}
for (; i < m; i++){
piv[i] = i;
}
pivsign = 1;
for(j = 0; j < n; j++){
ptrTmp1 = &LU[j];
ptrTmp2 = &LUcolj[0];
for(i = 0; i <= m - 4; i += 4){
*ptrTmp2++ = ptrTmp1[i * stride];
*ptrTmp2++ = ptrTmp1[(i + 1) * stride];
*ptrTmp2++ = ptrTmp1[(i + 2) * stride];
*ptrTmp2++ = ptrTmp1[(i + 3) * stride];
}
for (; i < m; i++){
*ptrTmp2++ = ptrTmp1[i * stride];
}
for(i = 0; i < m; i++ ){
ivf64 s = 0;
int kmax;
LUrowi = &LU[i * stride];
kmax = (i < j)? i : j;
#if defined(X86_SSE_OPTED)
{
Array1D_mul_sum_real64(LUcolj, kmax, LUrowi, &s);
}
#else
for(k = 0; k < kmax; k++){
s += LUrowi[k] * LUcolj[k];
}
#endif
LUrowi[j] = LUcolj[i] -= s;
}
// Find pivot and exchange if necessary.
p = j;
max_value = fabsl(LUcolj[p]);
for(i = j + 1; i < m; ++i ){
ivf64 t = fabsl(LUcolj[i]);
if (t > max_value){
max_value = t;
p = i;
}
}
if( p != j ){
ptrTmp1 = &LU[p * stride];
ptrTmp2 = &LU[j * stride];
#if defined(X86_SSE_OPTED)
{
__m128d t1,t2,t3,t4,t5,t6,t7,t8;
for (k = 0; k <= n - 8; k += 8){
t1 = _mm_load_pd(&ptrTmp1[0]);
t2 = _mm_load_pd(&ptrTmp1[2]);
t3 = _mm_load_pd(&ptrTmp1[4]);
t4 = _mm_load_pd(&ptrTmp1[6]);
t5 = _mm_load_pd(&ptrTmp2[0]);
t6 = _mm_load_pd(&ptrTmp2[2]);
t7 = _mm_load_pd(&ptrTmp2[4]);
t8 = _mm_load_pd(&ptrTmp2[6]);
_mm_store_pd(&ptrTmp2[0], t1);
_mm_store_pd(&ptrTmp2[2], t2);
_mm_store_pd(&ptrTmp2[4], t3);
_mm_store_pd(&ptrTmp2[6], t4);
_mm_store_pd(&ptrTmp1[0], t5);
_mm_store_pd(&ptrTmp1[2], t6);
_mm_store_pd(&ptrTmp1[4], t7);
_mm_store_pd(&ptrTmp1[6], t8);
ptrTmp1 += 8;
ptrTmp2 += 8;
}
for (; k < n; k++){
FIV_SWAP( ptrTmp1[0], ptrTmp2[0], ivf64);
ptrTmp1++,ptrTmp2++;
}
}
#else
for(k = 0; k <= n - 4; k += 4 ){
FIV_SWAP( ptrTmp1[k + 0], ptrTmp2[k + 0], ivf64);
FIV_SWAP( ptrTmp1[k + 1], ptrTmp2[k + 1], ivf64);
FIV_SWAP( ptrTmp1[k + 2], ptrTmp2[k + 2], ivf64);
FIV_SWAP( ptrTmp1[k + 3], ptrTmp2[k + 3], ivf64);
}
for (; k < n; k++){
FIV_SWAP( ptrTmp1[k], ptrTmp2[k], ivf64);
}
#endif
k = piv[p];
piv[p] = piv[j];
piv[j] = k;
pivsign = -pivsign;
}
if( (j < m) && ( LU[j * stride + j] != 0 )){
ivf64 t = 1.0 / LU[j * stride + j];
ptrTmp1 = &LU[j];
for(i = j + 1; i <= m - 4; i +=4 ){
ivf64 t1 = ptrTmp1[(i + 0)* stride];
ivf64 t2 = ptrTmp1[(i + 1) * stride];
ivf64 t3 = ptrTmp1[(i + 2) * stride];
ivf64 t4 = ptrTmp1[(i + 3) * stride];
t1 *= t, t2 *= t, t3 *= t, t4 *= t;
ptrTmp1[(i + 0) * stride] = t1;
ptrTmp1[(i + 1) * stride] = t2;
ptrTmp1[(i + 2) * stride] = t3;
ptrTmp1[(i + 3) * stride] = t4;
}
for(; i < m; i++ ){
ptrTmp1[i * stride] *= t;
}
}
}
}
void low_tri_solve(ivf64* L, int stride_L, ivf64* U, int row_u, int coln_u, int stride_u)
{
int i,j,k;
for (k = 0; k < row_u; k++){
ivf64* ptr_t2 = &L[k];
for (i = k + 1; i < row_u; i++){
ivf64 t3 = ptr_t2[i * stride_L];
ivf64* ptr_t4 = &U[i * stride_u];
ivf64* ptr_t1 = &U[k * stride_u];
#if defined(X86_SSE_OPTED)
__m128d m_t1,m_t2,m_t3,m_t4,m_t5,m_t6,m_t7,m_t8,m_t3_t3;
m_t3_t3 = _mm_set1_pd(t3);
for (j = 0; j <= coln_u - 8; j += 8){
m_t1 = _mm_load_pd(&ptr_t1[0]);
m_t2 = _mm_load_pd(&ptr_t1[2]);
m_t3 = _mm_load_pd(&ptr_t1[4]);
m_t4 = _mm_load_pd(&ptr_t1[6]);
ptr_t1 += 8;
m_t1 = _mm_mul_pd(m_t1, m_t3_t3);
m_t2 = _mm_mul_pd(m_t2, m_t3_t3);
m_t3 = _mm_mul_pd(m_t3, m_t3_t3);
m_t4 = _mm_mul_pd(m_t4, m_t3_t3);
m_t5 = _mm_load_pd(&ptr_t4[0]);
m_t6 = _mm_load_pd(&ptr_t4[2]);
m_t7 = _mm_load_pd(&ptr_t4[4]);
m_t8 = _mm_load_pd(&ptr_t4[6]);
m_t5 = _mm_sub_pd(m_t5, m_t1);
m_t6 = _mm_sub_pd(m_t6, m_t2);
m_t7 = _mm_sub_pd(m_t7, m_t3);
m_t8 = _mm_sub_pd(m_t8, m_t4);
_mm_store_pd(&ptr_t4[0], m_t5);
_mm_store_pd(&ptr_t4[2], m_t6);
_mm_store_pd(&ptr_t4[4], m_t7);
_mm_store_pd(&ptr_t4[6], m_t8);
ptr_t4 += 8;
}
#else
for (j = 0; j <= coln_u - 4; j += 4){
ptr_t4[0] -= ptr_t1[0]* t3;
ptr_t4[1] -= ptr_t1[1]* t3;
ptr_t4[2] -= ptr_t1[2]* t3;
ptr_t4[3] -= ptr_t1[3]* t3;
ptr_t1 += 4;
ptr_t4 += 4;
}
#endif
for (; j < coln_u; j++){
ptr_t4[0] -= ptr_t1[0]* t3;
ptr_t1++,ptr_t4++;
}
}
}
}
static ivf64* ptr_arr_t = NULL;
void swap_matrix_rows(ivf64* arr_data, int m, int n, int stride, iv32u* pivt, int pivt_size)
{
int i,j;
int loc_stride = n + (n & 1);
if (loc_stride < LU_DEC_BLOCK_SIZE){
loc_stride = LU_DEC_BLOCK_SIZE;
}
if (ptr_arr_t == NULL){
ptr_arr_t = fIv_malloc(loc_stride * sizeof(ivf64) * m);
}
for (i = 0; i < m; i++){
ivf64* ptr_src = arr_data + i * stride;
ivf64* ptr_dst = ptr_arr_t + i * loc_stride;
#if defined(X86_SSE_OPTED)
__m128d t1,t2,t3,t4,t5,t6,t7,t8;
for (j = 0; j <= n - 16; j += 16){
t1 = _mm_load_pd(&ptr_src[0]);
t2 = _mm_load_pd(&ptr_src[2]);
t3 = _mm_load_pd(&ptr_src[4]);
t4 = _mm_load_pd(&ptr_src[6]);
t5 = _mm_load_pd(&ptr_src[8]);
t6 = _mm_load_pd(&ptr_src[10]);
t7 = _mm_load_pd(&ptr_src[12]);
t8 = _mm_load_pd(&ptr_src[14]);
ptr_src += 16;
_mm_store_pd(&ptr_dst[0], t1);
_mm_store_pd(&ptr_dst[2], t2);
_mm_store_pd(&ptr_dst[4], t3);
_mm_store_pd(&ptr_dst[6], t4);
_mm_store_pd(&ptr_dst[8], t5);
_mm_store_pd(&ptr_dst[10], t6);
_mm_store_pd(&ptr_dst[12], t7);
_mm_store_pd(&ptr_dst[14], t8);
ptr_dst += 16;
}
for (; j < n; j++){
*ptr_dst++ = *ptr_src++;
}
#else
memcpy(ptr_dst, ptr_src, n * sizeof(ivf64));
#endif
}
for (i = 0; i < m; i++){
ivf64* ptr_src = ptr_arr_t + pivt[i] * loc_stride;
ivf64* ptr_dst = arr_data + i * stride;
#if defined(X86_SSE_OPTED)
__m128d t1,t2,t3,t4,t5,t6,t7,t8;
for (j = 0; j <= n - 16; j += 16){
t1 = _mm_load_pd(&ptr_src[0]);
t2 = _mm_load_pd(&ptr_src[2]);
t3 = _mm_load_pd(&ptr_src[4]);
t4 = _mm_load_pd(&ptr_src[6]);
t5 = _mm_load_pd(&ptr_src[8]);
t6 = _mm_load_pd(&ptr_src[10]);
t7 = _mm_load_pd(&ptr_src[12]);
t8 = _mm_load_pd(&ptr_src[14]);
ptr_src += 16;
_mm_store_pd(&ptr_dst[0], t1);
_mm_store_pd(&ptr_dst[2], t2);
_mm_store_pd(&ptr_dst[4], t3);
_mm_store_pd(&ptr_dst[6], t4);
_mm_store_pd(&ptr_dst[8], t5);
_mm_store_pd(&ptr_dst[10], t6);
_mm_store_pd(&ptr_dst[12], t7);
_mm_store_pd(&ptr_dst[14], t8);
ptr_dst += 16;
}
for (; j < n; j++){
*ptr_dst++ = *ptr_src++;
}
#else
memcpy(ptr_dst, ptr_src, n * sizeof(ivf64));
#endif
}
}void matrix_sub_matrix_mul(real64* A22, real64* L21, int row_L21,int col_L21, int stirde,
real64* U12, int col_U21)
{
int i,j,k;
for (j = 0; j < row_L21; j++){
real64* pTmp_A = &L21[j * stirde];
real64* pTmp_C0 = &A22[j * stirde];
for (k = 0; k < col_L21; k++){
real64 t_A_d = -pTmp_A[k];
real64* pTmp_B = &U12[k * stirde];
for (i = 0; i <= col_U21 - 4; i += 4){
pTmp_C0[i + 0] += t_A_d * pTmp_B[i + 0];
pTmp_C0[i + 1] += t_A_d * pTmp_B[i + 1];
pTmp_C0[i + 2] += t_A_d * pTmp_B[i + 2];
pTmp_C0[i + 3] += t_A_d * pTmp_B[i + 3];
}
for (; i < col_U21; i++){
pTmp_C0[i] += t_A_d * pTmp_B[i];
}
}
}
}