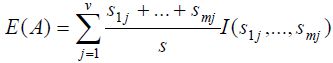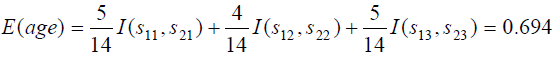实习了一段时间，接触了一些数据挖掘、机器学习的算法，先记录下来方便以后的复习回顾：
一：决策树概念
决策树可以看做一个树状预测模型，它是由节点和有向边组成的层次结构。树中包含3中节点：根节点、内部节点、叶子节点。决策树只有一个根节点，是全体训练数据的集合。树中每个内部节点都是一个分裂问题：指定了对实例的某个属性的测试，它将到达该节点的样本按照某个特定的属性进行分割，并且该节点的每一个后继分支对应于该属性的一个可能值。每个叶子节点是带有分类标签的数据集合即为实例所属的分类。
决策树算法很多，例如：ID3、C4.5、CART等。这些算法均采用自上而下的贪婪算法，每个内部节点选择分类效果最好的属性来分裂节点，可以分成两个或者更多的子节点，继续此过程直到这棵决策树能够将全部的训练数据准确的分类，或所有属性都被用到为止。该算法的简化版本是在使用了全部样本的假设来构建决策树的。具体步骤如下：
（1）：假设T为训练样本集。
（2）：从属性集合Attributes中选择一个最能区别T中样本的属性。
（3）：创建一个树节点，它的值为所选择的属性。创建此节点的子节点，每个子链代表所选属性的一个唯一值（唯一区间），使用子链的值进一步将样本细分为子类。
对于每一个分支继续重复（2）（3）的过程，直到满足以下两个条件之一：
(a):所有属性已经被这条路径包括。
(b):与这个节点关联的所有训练样本都具有相同的目标属性（熵为0）。
下面借用《数据挖掘概念与技术》书中的一个列子来方便理解：
图1-1
图1-1是一个典型的决策树，它表示概念buys_computer,即它目的是预测顾客是否可能购买计算机。内部节点用矩形表示，叶子节点用椭圆表示。
为了对未知的样本分类，样本的属性值在决策树上测试。我们用一些训练样本构造了图1-1中的决策树，每个内部节点表示一个属性上的测试，每个叶子节点代表一个分类（buys_computer = yes, buys_computer = no ）.
二：决策树的适用情况
通常决策树学习最适合具有以下特征的问题：
（1）：实例是由“属性-值”对表示的。
（2）：目标函数具有离散的输出值。例如上面的yes和no
（3）：实例的所有属性都是离散值。如果是连续值或者离散值种类太多，可以把它分为不同的区间，例如上面的age分为了3个区间而不是每个独立的值为一个判断分支。
三：决策属性的选择
建树算法中属性的选择非常重要。属性选择方法很多种，例如信息增益（information gain）、信息增益比（information gain ratio）、Gini 指标（Gini Index）等方法。
ID3算法依据的是信息增益来选择属性,每次计算所有剩余候选属性的信息增益，然后根据信息增益最大的一个作为此次的分类属性。信息增益是用熵作为尺度，是衡量属性对训练数据分类能力的标准。
假设表3-1为图1-1中的训练样本集：共有14条数据，属性有：age、income、student、credit_rating,目标属性是：buys_computer
表3-1
下面根据表3-1和图1-1的例子来讲解某具体属性的信息增益的计算过程：
对于某个具体的属性A，它的信息增益计算表达式是：
（1）
是对给定样本分类所需的期望信息，计算过程如下：
设S是s个训练样本的集合，S也就是对于表3-1中的数据，s = 14。假定类标号属性有m个不同值，定义m个不同类Ci（i=1,2,...m）.设si是类Ci中的样本数，对应表3-1和图1-1实例中m=2,其中 C1 = yes C2 = no s1 = 9 s2 = 5 。
则：
其中pi是任意样本属于Ci的概率，pi = si/s .公式中的对数函数以2为底，因为信息用二进位编码。
在该实例中 
（2）
是根据A划分子集的熵或期望值，计算过程如下：
设属性A有v个不同的值{a1,...av},对应实例中的数据，例如属性age，分为3个不同的值:
a1为 <=30
a2为 30..40
a3为 >40 ;
属性A把训练样本集合S划分为v个子集{S1,...Sv};其中Sj包含训练样本集S中在属性A上有值aj的样本。Sij是子集Sj中属于类Ci的样本数。
其中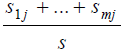
充当第j个子集的权值，等于子集（即A值为aj）的样本总数除以S中的样本总数 即 Sj/S。
对于给定的子集Sj有
其中，Pij=Sij/Sj ,是Sj中的样本属于Ci的概率。
该实例中：
因此属性age的信息增益为：Gain（age）= I（s1,s2） - E(age) = 0.246
类似的我们可以计算出Gain(income)=0.029 Gain(student)=0.151 Gain(credit_rating)=0.048.由于age在属性中具有最高信息增益，因此它被选作为第一个测试属性。
图1-1是最终生成的决策树。
四：决策树的剪枝
为了防止决策树和训练样本集的过度拟合，需要对决策树进行剪枝。剪枝通常有事先剪枝法和事后剪枝法。
事先剪枝法： 是建树过程中判断当前节点是否需要继续划分的剪枝方法。通常是通过重要性检测判断是否停止分裂节点。
事后剪枝法： 是让树充分生长之后，再判断是否将某些分支变成节点。常用方法是根据错误分裂率（或者决策树编码长度）进行决策树的事后修剪。
参考资料：机器学习 Mitchell T.M
数据挖掘：概念与技术 第三版 Jiawei Han