最小生成树之克鲁斯卡尔（kruskal）算法

 Kruskal算法

前面讲了最小生成树的Prim算法的实现思路是，通过顶点的扩展不断地寻找最小权重的生成树，而Kruskal算法是查找最小权值的边，然后逐渐把连通分量变为一个联结全部顶点的最小生成树。

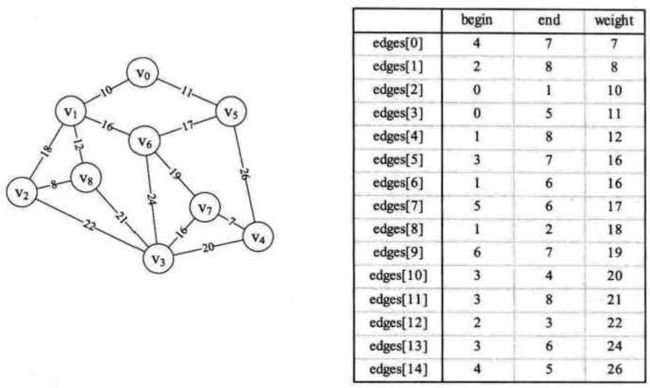
不同于 Prim算法 ，这次用边集数组结构来实现 Kruskal算法 

结构很简单，包括权值，边的弧起点和终点的下标

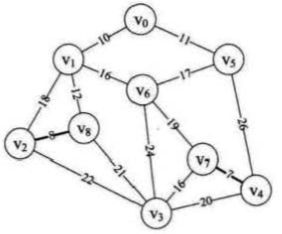
将前面Prim例子中的图转化为边集数组，并且按照权值升序排列储存为 edges[] 这样一个数组，那么这样做的意义就在于后面按照权值的顺序来安排边，代码如下：

 1 void MiniSpanTree_Kruskal(MGraph G)
 2 {
 3     int i,n,m;
 4     Edge edges[MAXVEX];
 5     int parent[MAXVEX];
 6     //这里省略构造edges数组时的排序步骤代码
 7     for(i = 0;i < G.numVertexes;i++)
 8     {
 9         parent[i] = 0;
10     }
11     for(i = 0;i < G.numEdges;i++)
12     {
13         n = Find(parent,edges[i].begin);
14         m = Find(parent,edgws[i].end);
15         if(n != m)
16         {
17             parent[n] = m;
18             //将这一条边的结尾顶点下标存在数组起点下标的位置
19             printf("(%d %d) %d",edges[i].begin,edges[i].end,edges[i].weight);
20         }
21     }
22 }
23 
24 int Find(int *parent,int f)
25 {
26     while(parent[f] > 0)
27         f = parent[f];
28     return f;
29 }

我们来读一哈这个代码：

3~10行定义边集数组以及初始化 parent 数组，后面详细讲解这个数组的用处

代码结构较为简单，故讲解11~22行循环，夹杂 Find 函数实现

第一次循环： n = 4 ,m = 7, parent = {0,0,0,0,7,0,0,0,0,0,0,0,0,0,0} ,然后打印边的起点终点和权值，此时 parent 数组以数字下标位置和内容表示（v4 v7）这条边已经加入豪华最小生成树

第二次循环：n = 2 ,m = 8, parent = {0,0,8,0,7,0,0,0,0,0,0,0,0,0,0} ,然后打印边的起点终点和权值，此时 parent 数组以数字下标位置和内容表示（v2 v8）这条边已经加入豪华最小生成树

 

 第三次循环：n = 0 ,m = 1, parent = {0,1,8,0,7,0,0,0,0,0,0,0,0,0,0} ,然后打印边的起点终点和权值，此时 parent 数组以数字下标位置和内容表示（v0 v1）这条边已经加入豪华最小生成树

 第三、四、五、六次循环：因为循环中的判断条件和之前一样, 故第六次循环后parent = {1,5,8,7,7,8,0,0,6,0,0,0,0,0,0} ,然后不断打印边（v0,v5）（v1,v8）（v3,v7）（v1,v6）的起点终点和权值

当 i = 7 时，我们会发现对应的是 (v5 v6)这条边，如果打印这条边，则会生成闭环，就不符合我们最小生成树的结构要求，那么我们来跑一下 11行的循环， 调用Find函数，会传入参数 edges[7].begin = 5，此时 Find函数内部，parent[5] = 8，大于0， m = f = parent[8] = 6，而 edges[7].end = 6，传入Find 得 n = 6，此时m = n，不打印结点信息，（否则将形成闭环）

后面的 i = 8、 i = 9均为闭环所以均不打印

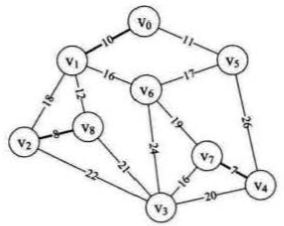
生成树为

Kruskal算法总结：

假设 N= (V，{E})是连通网，则令最小生成树的初始状态为只有 n 个顶点而无边的非连通图 T={V，{}}，图中每个顶点自成一个连通分量。在 E 中选择代价最小的边，若该边依附的顶点落在 T 中不同的连通分量上，则将此边加入到 T 中，否则舍去此边而选择下一条代价最小的边。依次类推，直至 T 中所有顶点都在同一连通分量上为止。
此算法的 Find 函数由边数 e 决定，时间复杂度为 O(loge)而外面有一个 for 循环 e 次。 所以克鲁斯卡尔算法的时间复杂度为 O(eloge).
对比两个算法，Kruskal算法主要是针对边来展开，边数少时效率会非常高，所以对于稀疏图有很大的优势，而Prim算法对于稠密图，即边数非常多的情况会更好一些。

 

转载于:https://www.cnblogs.com/yx1999/p/10362394.html