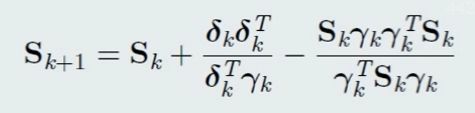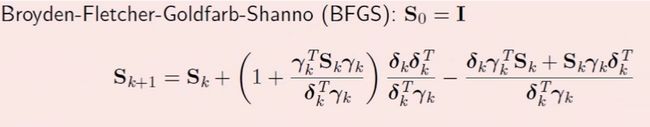机器学习数学知识积累总结

本篇博文来自学习稀牛学院AI数学课程中的学习笔记

引子：房价预测

给定一组房价数据$x^{(i)},y^{(i)}$,其中x可以是标量scala,也可以是向量，比如可以为房屋面积，还可以包含房屋年龄，地段等信息，y为房屋价格。我们需要找出x和y之间的关系，也就是一个模型，将来给定输入的一个未知数据，我们可以预测房价。模型可以先以线性回归模型$y= \omega x + b$作为预设的模型，我们的任务就是要根据已知的数据来求解对应的$\omega和b$模型参数。

无约束优化问题

房价预测问题，我们可以抽象为以下无约束优化问题：

•  如果自变量x为标量，比如只包含一个面积特征的话，我们的模型就是$f: R \rightarrow R$,目标为:$min f(x) \; x \in R$
• 如果自变量为向量，则我们的模型就是$f: R^n \rightarrow R$,我们的目标就是$min f(x) \; x \in R^n$

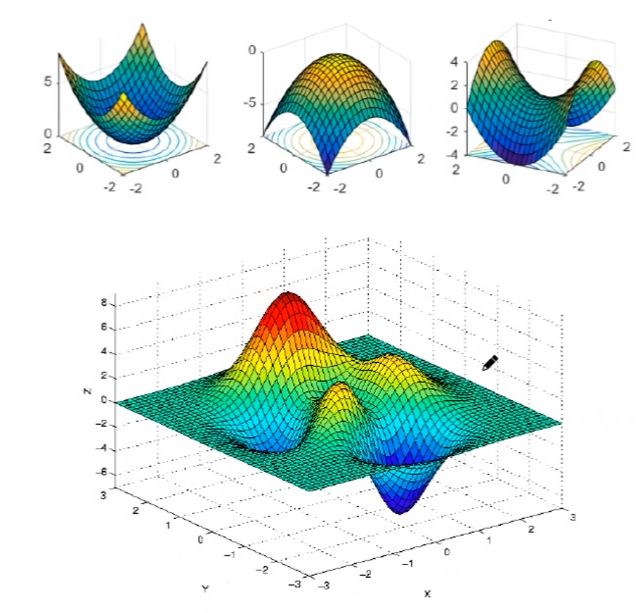
优化问题中的极值点情况

全局最大，全局最小；

局部最大，局部最小；

既不是最大也不是最小的驻点---鞍点

实际优化中绝大部分都是局部极值的优化问题!

 

导数，梯度，Hessian海森矩阵

一阶情况

如果函数自变量为为标量，其一阶导数我们很熟悉$f'(x)$.例如$(x^2)'=2$

相应地，如果函数的自变量为向量，这时其一阶导数就是梯度$g(X) = \triangledown f(X) = \frac{\partial f(X)}{\partial X} = \begin{bmatrix}\frac{\partial f(x)}{\partial x_1}\\ ...\\ \frac{\partial f(x)}{\partial x_n}\end{bmatrix}$，例如$z=x^2+y^2$其梯度就为$\triangledown (x^2+y^2) = \begin{bmatrix} 2x\\ 2y\end{bmatrix}$

二阶情况

如果函数的自变量为标量，其二阶导数我们会非常熟悉$f"(x)$，例如$(x^2)"=2$

相应地，如果函数的自变量为向量，这时其二阶导数就称为海森矩阵

$H(X)=\triangledown ^2 f(x) = \begin{bmatrix} \frac{\partial ^2 f(x)}{\partial ^2 x_1} & \frac{\partial ^2 f(x)}{\partial x_1 \partial x_2} & ... & \frac{\partial ^2 f(x)}{\partial x_1 \partial x_n}\\ \frac{\partial ^2 f(x)}{\partial x_2 \partial x_1} & \frac{\partial ^2 f(x)}{\partial ^2 x_2}& ... & \frac{\partial ^2 f(x)}{\partial x_2 \partial x_n}\\ ... & ... & ... & ... \\ \frac{\partial ^2 f(x)}{\partial x_n \partial x_1} & \frac{\partial ^2 f(x)}{\partial x_n \partial x_2} & ... & \frac{\partial ^2 f(x)}{\partial ^2 x_n} \end{bmatrix}$

比如函数$z=x^2+y^2+\omega^2+2xy+2x\omega+2y\omega$，其对应的海森矩阵就是

$\begin{bmatrix}2 & 2 & 2\\2 & 2 &2 \\2 & 2 &2 \end{bmatrix}$

海森矩阵是一个$(n,n)$的对称矩阵

二次型

给定矩阵$A \in R^{nxn}$,以下函数形式

$X^TAX= \sum_{i=1}^{n}x_i(AX)_i=\sum_{i=1}^{n}x_i(\sum_{j=1}^{n}a_{ij}x_j) = \sum_{i=1}^{n}\sum_{j=1}^{n}x_ix_ja_{ij}$

被称为二次型。比如$x_1^2+x_2^2+x_3^2+2x_1x_3$ 这种所有项都是二次齐次形式的式子被称为二次型。

一般来说，只要提到二次型，其对应的矩阵A就是对称矩阵。

比如$f(x) = x_1^2+x_2^2+x_3^2$其对应的矩阵$A$就为

$\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 &1 \end{bmatrix}$ 

矩阵的正定负定及不定

给定一个对称矩阵$A\in R^{nxn}$，(因为正定往往用于矩阵伴随的二次型正负的判定，因此我们只研究对称矩阵的正定性)，如果对于所有$x\in R^n$,都有其二次型$X^TAX \geq 0$则称矩阵$A$为半正定矩阵；此时，其特征值都是非负数，即$\lambda(A) \geq 0$.

如果对于所有非0 的x，其二次型都是正数，这时我们称矩阵为正定矩阵

由于海森矩阵是对称矩阵，因此海森矩阵就可以研究其正定和负定特性了。

当海森矩阵为正定时，其二次型就是正数，其特征值就是大于0

二次型梯度计算

对于向量$a,x$，对称矩阵$A$,有以下的梯度计算公式:

$\triangledown (a^TX) = a, \triangledown ^2(a^TX)=0$

 $\triangledown (X^TAX) = 2 AX, \triangledown ^2 (X^TAX) = 2A $

最小二乘及其梯度计算

$f(X) = ||AX -b||^2_2=(AX-b)^T(AX-b)=X^TA^TAX-2b^TAX + b^Tb$

$\triangledown f(X) = \triangledown (||AX -b||^2_2)= 2A^TAX-2A^Tb$

再比如$\triangledown f(X) = \triangledown (X^TAX+2b^TX+c) = 2AX+2b$

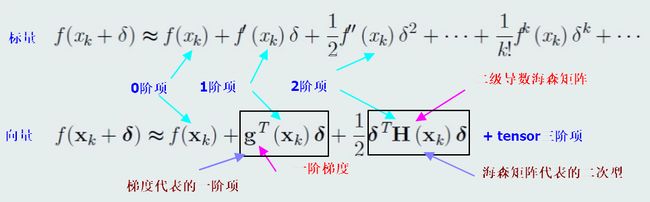
函数的泰勒级数展开

使用泰勒级数展开研究函数的极值

当只保留泰勒级数一阶项时，我们研究使得$f(x_k+\delta) \ge f(x_k)$，则一阶导数(梯度)必须为0，因为$\delta$可以大于0，也可以小于0，要保证$f(x_k+\delta) \ge f(x_k)$则必须有梯度等于0

梯度等于0是在$x_k$处取得极值的必要条件。要研究其是极大还是极小值，我们需要继续研究二阶项，如果$f''(x_k) > 0$则取得极小值，相反，如果$f''(x_k) < 0$则在$x_k$处取得极大值

针对输入为向量的情况是类似的：

梯度$g(x_k) = 0$求得的$x_k$是候选驻点，要研究极大极小甚至鞍点需要看二次项，也就是二次型$\delta ^TH(x_k)\delta$的正负性，这可以由$f(x)$的二阶导数海森矩阵的正定负定来判断:

当$H(x_k) \succ 0$正定时，$x_k$这一点为局部极小点(反之则为局部最大点)。如果$H(x_k)$是一个不定矩阵，则是一个鞍点。

函数极值的解析解法

1. 令梯度$\triangledown f(x) =0$，求解得到平衡点(驻点)

2. 计算驻点对应的海森矩阵，判断其正定性：如果是正定则是极小值，如果负定则是极大值，如果不定则是鞍点

无约束优化数值计算迭代法

由于解析解大多数情况下无法直接求得，因此人们发明了优化迭代的数值计算方法

一般步骤:

1. 选择一个初始点，设置一个收敛容差 $\epsilon $,计数$k=0$

2.决定搜索方向$d_k$，使得函数在该方向迭代时数值下降。这是不同优化算法最核心的差别!

3.决定步长$\alpha_k$（学习率），使得$f(x_k+\alpha_kd_k)$对于$\alpha_k \ge 0$最小化(也就是求得最优的步长！因为步长太小则优化收敛的速度太慢，步长太大，则有可能造成震荡冲过极值点)，构建$x_{k+1} = x_k+ \alpha_kd_k$

4.如果$||d_k|| < \epsilon$则停止输出$x_{k+1}$；否则继续重复迭代

梯度下降法

我们先省略掉学习率，只考虑迭代方向的影响因素，通过泰勒级数我们知道

$f(x_k+d_k)\approx f(x_k) + g^T(x_k)d_k$,其中$f(x_k),g^T(x_k)$都是常数，要使得$f(x_k+d_k)$下降变小，则须在$f(x_k)$加上一个负数，而$g^T(x_k)d_k$实际上就是两个向量内积，我们知道当向量方向相反时内积为负并且内积绝对值最大其值为$||-g(x_k)||^2$，自然我们可以选择$d_k = -g^T(x_k)$这时函数$f(x_k+d_k)$在$x_k$点将下降的最快！

牛顿法

在梯度下降法中，为简化问题，我们直接把泰勒级数的二阶项省略，通过选取负梯度方向作为迭代方向。但是我们知道二阶项一般来说并不是非常小（虽然相对一阶项来说确实够小），因此直接使用梯度下降法中选取的一阶梯度负方向可能并不是$f(x)$的全局最优方向。牛顿法就是将二阶项添加进泰勒级数展开式从而探究最优迭代方向的成果。

$f(x_k+d_k)\approx f(x_k) + g^T(x_k)d_k + \frac{1}{2}d^T_kH(x_k)d_k$

上面的泰勒展开中，只有$d_k$为未知量，我们将$f(x_k+d_k)$视为$d_k$的函数，来寻找最优的迭代方向:

$d_k = \underset{d_k}{argmin}(f(x_k+d_k))$,

令$\frac{\partial f(x_k+d_k)}{\partial d_k} = 0\Rightarrow g(x_k)+H(x_k)d_k=0$,

如果海森矩阵是正定矩阵，我们可以选择$d_k = -H^{-1}(x_k)g(x_k)$ ，带入$f(x_k+d_k)$必然得出其值小于$f(x_k)$

也就是说，当海森矩阵$H(x_k)$为正定时，$d_k = -H^{-1}(x_k)g(x_k)$就是使得函数下降最快的方向！！

这个方向将会比梯度下降法中的负梯度方向更加精准(因为泰勒展开更加精准，因此下降方向将更加准确！)，因此迭代收敛必将更快!

拟牛顿法

虽然牛顿法理论上非常棒，但是工程中有以下问题:

1. 如果实际工程中的维数n较大，而海森矩阵H本身是nXn的矩阵就将变得更加庞大，

2. $H^-1$非常难求。

3.牛顿法中要求海森矩阵在$x_k$点是正定矩阵，本身这就比较难以满足

因此，聪明的数学家就发明了拟牛顿法.其解决思路为:

当海森矩阵H不是正定矩阵时，可以对H矩阵进行修正：

 $H(x_k)+E,E=\delta I, \delta > 0$, delta很小。矩阵的特征值有以下性质：矩阵加上一个单位阵以后其特征值也将加上delta

拟牛顿方的核心思想是使用一阶的量去近似逼近二阶的量(H矩阵以及H矩阵的逆)。

我们先统一梯度下降法和牛顿法中对方向的选取:

$d_k = - S_kg_k$,其中$S_k = \left\{\begin{matrix} I & steppest(SGD))\\ H_k^{-1} & Newton \end{matrix}\right.$

我们定义$\delta_k = x_{k+1} - x_k, \gamma_k = g_{k+1}-g_k$,他们都是在第$k$步迭代时已知的值

我们用$S_{k+1}$去逼近H矩阵的逆，令迭代中,须满足$S_{k+1}\gamma_k = \delta _k$,通过微分的定义，我们知道$S_{k+1}$

实际上可以看做梯度对x变化的比值的导数，也就是海森矩阵的逆。

DFP

在DFP算法中，选择$\triangle S_k = \alpha u u^T + \beta vv^T$,其中我们需要注意的是$uu^T$实际上是rank为1的矩阵！

计算出来每一步迭代时的$S_k$后再算出$d_k$就是更新的方向

BFGS

线性回归问题求解

有了上面介绍的矩阵梯度及优化方法，我们再回过头来看看房价预测的线性回归问题求解。

学习的目标: $f(x) = \omega ^Tx +b$，使得$f(x^{(i)}) \approx y^{(i)}$,为了方便计算，我们全部整合为一个矩阵乘法：

$$\bar \omega = \begin{bmatrix} \omega \\ b \end{bmatrix} X = \begin{bmatrix} x^{(1)T}& 1\\ ... & ... \\ x^{(N)T}& 1 \end{bmatrix}_{NX(d+1)}$$

也就是说我们的目标是求解参数$\bar \omega$使得:$y \approx X \bar \omega$

为此，我们定义2范数平方损失函数，求解使得该损失函数最小化的参数

$min ||y-X \omega||^2_2$

• 解析方式求解:

　　令 $g(\bar \omega) = 0 \Rightarrow 2X^T(X \bar \omega - y)=0  \Rightarrow \omega ^* = (X^TX)^{-1}X^Ty  $

• 梯度下降法

$g(\bar W) = 2X^T(X \bar W -y)=2 \sum_{i=1}^{N}x^{(i)}(W^Tx^{(i)}-y^{(i)})$

$\bar W \leftarrow \bar W - \alpha g(\bar W)$

• 随机梯度下降法SGD

由于梯度下降法每次迭代时，所有的样本数据都参与计算，如果样本量很大的话，迭代非常缓慢，因此实际工程中可能使用随机梯度下降法，每一个样本都做一次迭代。但是这可能导致抖动比较大

$g(\bar W) = 2X^T(X \bar W -y)=2 x^{(i)}(W^Tx^{(i)}-y^{(i)})$

• min-batch 随机梯度下降法

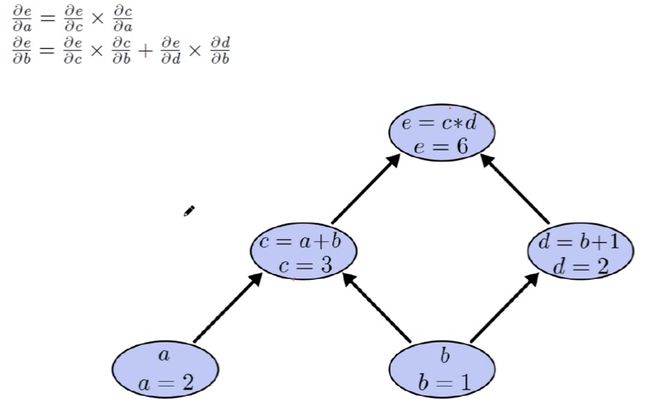
BP算法求导加法注意事项

凸优化

凸集，仿射集

仿射集:如果一个集合$C  \in R^n$是仿射的，则$C$中任意两点间的直线也在该集合中，也就是

$x = \theta x_1 + (1- \theta) x_2 \in C, \theta \in R$

凸集:如果一个集合$C \in R^n$是凸的，则对于任意的$x,y \in C$, $\theta x + (1- \theta) y \in C, 0 \ge \theta \ge1$

仿射集必然是凸集， 凸集未必是仿射集

常见的凸集：

$R^n, R^n_+$，也就是说实数集和正，负实数集都是凸集

超平面： $C = \{ x|a^Tx = b \}$, 既是凸集又是仿射集 

半空间： $C = \{ x|a^Tx \ge b \}, C = \{ x|a^Tx \le b \}$是凸集

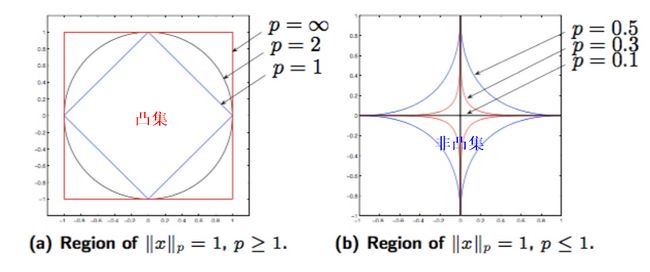
范数球：$||X||_2 \le 1$

 

向量范数:

• 2-norm: $||X||_2=\sqrt {\sum_{i=1}^{n}|x_i|^2}=(X^TX)^{1/2}$
• 1-norm $||X||_1=\sum_{i=1}^{n}|x_i|$，取分量绝对值之和
• $ \infty-norm $:  $||X||_\infty= max|x_i|$,取绝对值最大的分量
• p-norm, $p \ge 1$， $||X||_p= (\sum_{i=1}^{n}|x_i|^p)^{1/p}$ 通用形式

 以上范数为欧几里德范数，满足以下三条定理：

• $|| X || \ge 0$, 非负性
• $||\alpha X|| = |\alpha| || X||$，齐次性
• $|| x+y|| \le ||x|| + ||y||$ 三角不等式

还有一条零范数，是取向量非0元的个数 $||X||_0$, 比如[ 1, 0, 0,0,1]的零范数为2

凸集的性质

凸集的交集是凸集

比如， $S = \{||X|| \le 1, X \ge 0 \} $, 第一个是范数球为凸集，第二个为半空间，为凸集合，他们的交集也为凸集

凸集的并集不一定是凸集

由这个凸集的交集是凸集这个性质很容易得出：有限个半空间和半平面的交集为凸集

$P = \{ X| AX \le b, CX = d \}$为凸集

 

凸函数

 如果一个函数满足以下两点，我们就称之为凸函数:

• dom(f)(函数f的定义域)为凸集
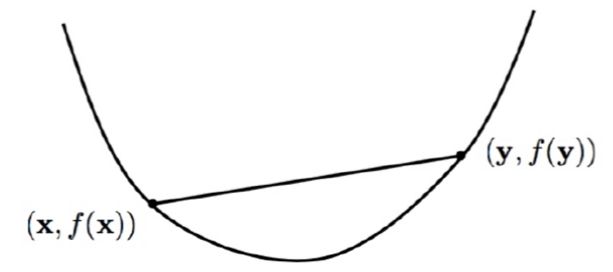
• 对于任何$x,y \in dom(f), 0 \le \theta \le 1$,都有$f(\theta x + (1- \theta) y) \le \theta f(x) +(1- \theta)f(y)$成立

其几何意义为: 连接函数曲线上的任何两点组成的线段都在函数的上方，这样的函数为凸函数

凸函数的局部最优解就是全局最优解

 

凸函数的判断准则

一阶充要条件: $f(x_1) \ge f(x) + \triangledown ^Tf(x)(x_1-x)$对于所有x1,x都成立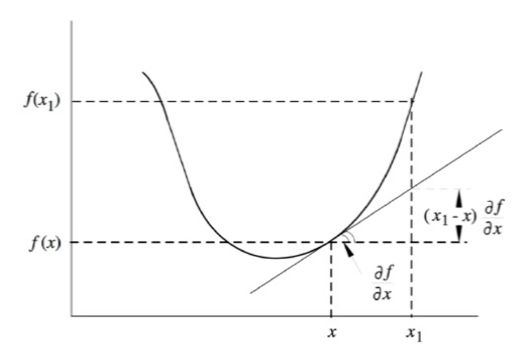

二阶充分必要条件: 如果函数f二阶可导，则函数f是凸函数的充分必要条件是其海森矩阵为非负定矩阵$H(x) \succeq 0$

凸函数举例

• $ax+b$
• $x^2$
• $-logx, x > 0$
• $xlogx x \ge 0$
• $f(x)=a^Tx+b$ 既凸又凹
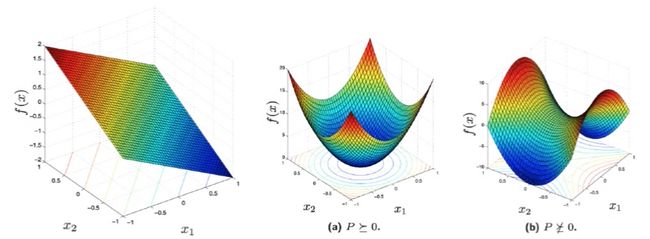
• $f(x) = X^TPX + 2q^TX + r$, 由于其海森矩阵为P，只要P为半正定矩阵，该函数就为凸函数
• $f(x) = ||X||^2_2 = X^TX$由于海森矩阵为$I$正定，因此2范数平方为凸函数

凸函数的性质

凸函数的局部最优解就是全局最优解

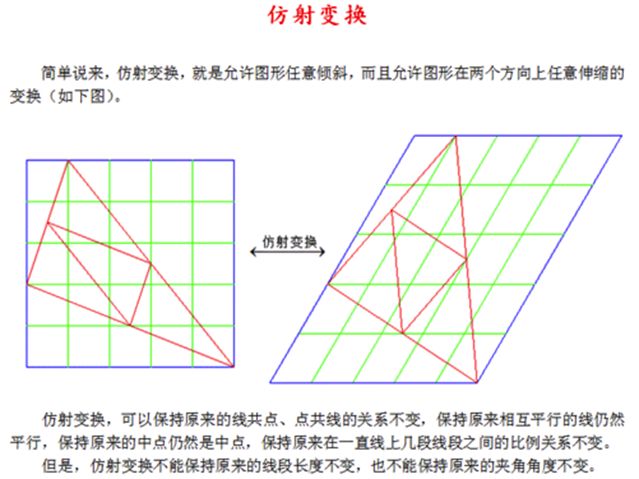
仿射变换补充知识:

仿射变换的公式表示:

 

保凸：

1. $f(x)$为凸函数，则自变量仿射变换后的函数$f(AX+b)$也为凸函数，例如: $||Y-AX||_2$为凸
2. g凸，h凸，如果h非递减，则复合函数$f(x)=h(g(x))$也是凸函数。比如$g(x)=||y-AX||_2$为凸函数,$h(x)=x^2$在$x \ge 0$部分非递减，那么$f(x)=||y-AX||^2_2$在$X \ge 0$为凸函数
3. f1,f2,..,fm为凸,$ w_1,w_2,...,w_m \ge 0$,则$w_1f_1+w_2f_2,+..,+w_mf_m$函数为凸，这一点非常重要！比如$f(x)=||y-AX||^2_2 + \gamma ||X||^2_2$为凸函数
4. 逐点最大: f1,f2,...,fm为凸，则$f(x) = max \{ f_1(x),f_2(x),..,f_m(x)\}$也为凸函数。对于连续情况同样适用。$f(x,y)$如果对于每个$y \in A$凸，则$sup_{y \in A}f(x,y)=max_{y \in A}f(x,y) = max \{(f(x,y_1),f(x,y_2),..f(x,y_m))\}$上确界为凸函数

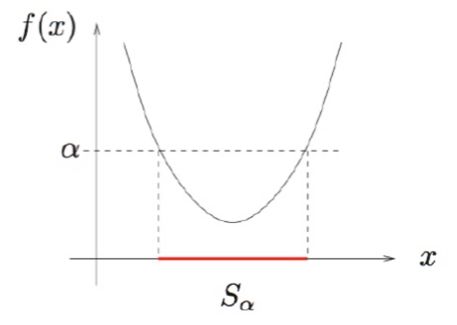
凸函数和凸集的关系：凸函数的$\alpha$水平集必然是凸集

$S_\alpha = \{ x|f(x) \le \alpha \}$

如果$f(x)$为凸函数，则上述$S_\alpha$为函数f的$\alpha$水平集，必然为凸集

凸优化问题标准形式

在机器学习中，最重要的一点是我们需要将实际问题抽象转化为一个数学的优化问题，一旦这个抽象转换完成，实际上问题就已经解决。特别地，如果我们能转化为一个凸优化问题，则更是能够得到全局最优解。因为对于优化问题，有非常成熟的数值计算方法迭代计算出对应的最优解。比如：如果是无约束优化问题，直接使用梯度下降，拟牛顿迭代等即可解决；对于有约束的优化问题，我们可以使用对偶理论将有约束问题转化为无约束优化问题后也可以使用对应的迭代算法求解。

本质上，凸优化就是在一个凸集上极小化一个凸的目标函数！

1. 问题的数学表达

minimize  $\; f_0(x)$

subject to :  $f_i(x) \le 0 ,i=1,2,..,m, h_i(x) = 0,i=1,2,..,p$

2. 是凸优化的条件:

• 目标函数$f_0(x)$是凸函数，可行域必须是凸集(也就是由约束条件定义的x可行域是凸集)
• 不等式约束函数$f_i(x)$是凸函数
• 等式约束函数$h_i(x)$是仿射函数，即$h_i(x) = AX+b$

典型的凸优化问题:

1. 线性规划问题 LP

minimize  $\; C^TX +d$

subject to :  $GX \le h , AX = b$

2. 二次规划问题(P半正定) QP

minimize  $\; 1/2 X^TPX + C^TX + d$

subject to :  $GX \le h AX = b$

3. QCQP(P, Qi均半正定)

minimize  $\; 1/2 X^TPX + C^TX+d$

subject to :  $1/2 X^TQ_iX + R_i^TX+S_i \le 0, i =1,2,3...m, AX = b$

 

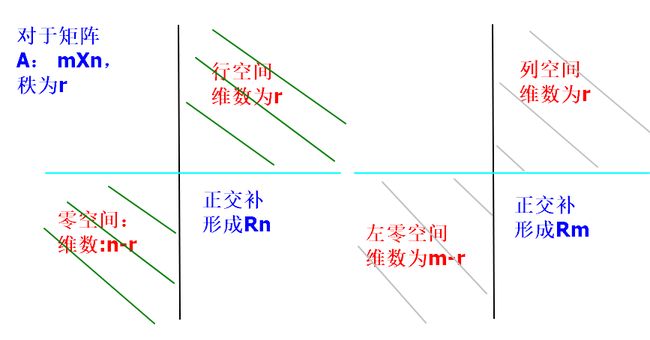
矩阵的4个子空间的关系

 

特征分解

对于方阵A如果满足$AX = \lambda X$，则称$\lambda$为A的特征值，X为特征向量；

对于$AX_i = \lambda X_i$,如果所有的特征值都不相同，则相应的所有的特征向量线性无关，此时矩阵A就可以被对角化为:

$A = V \Lambda V^{-1}$, 其中V为$[X_1,X_2,..,X_n]$是对应的特征向量, $\Lambda = Diag(\lambda_1,..,\lambda_n)$

 

实对称矩阵的对角化

实对称矩阵$A$的优良性质

1. $A$的所有特征值为实数；

2.$A$的不同特征值所对应的特征向量不但线性无关，而且相互正交,也就是说特征向量组成的矩阵U为正交矩阵。即:$A=U \Lambda U^T ,UU^T=U^TU=I$

定理： 设$A$为n阶实对称矩阵，则必然存在正交矩阵$P$,使得$PAP^{-1}=diag(\lambda_1, \lambda_2,...,\lambda_n)$，其中$\lambda_1, \lambda_2,...,\lambda_n$为矩阵$A$的特征值，

也就是说实对称矩阵可以被正交对角化

对角化过程:

1. 求解A的特征值；

2.求对应于每个特征值的特征向量：通过以下方程求解$(\lambda I - A)x=0$得到基础解系。对于单特征值，只需将属于它的特征向量规范化；对于r重特征值，需要先求出属于它的r个线性无关的特征向量，然后对这r个特征向量进行正交规范化，这样就可以得到n个两两正交的单位特征向量；

3.以正交规范化的特征向量为列组成矩阵，他就是要求解的矩阵P

$A = U \Lambda U^T = [u_1,..,u_n]\begin{bmatrix} \lambda_1 & & \\ & ... & \\ & & \lambda_n \end{bmatrix}\begin{bmatrix} u_1^T\\ ...\\ u_n^T \end{bmatrix}=\sum_{i=1}^{n}\lambda_iu_iu_i^T$

特征值可以视作某种能量，能量越大，则对应的占比就更大

https://wenku.baidu.com/view/5a3f1a234b35eefdc8d333f1.html

https://wenku.baidu.com/view/5fcd300810a6f524ccbf8532.

对称矩阵特征分解和子空间的关系

从$max(X^TAX), ||X||^2_2=1$优化问题来看特征值

我们可以通过拉格朗日对偶$L(X,\lambda) = X^TAX-\lambda X^TX$,计算梯度令其为0，$\bigtriangledown L(X, \lambda) = 2AX -2 \lambda X =0 \Rightarrow AX = \lambda X$

从上面的式子可以看出要最大化 $X^TAX$，必须使得X满足$AX = \lambda X$,将已知条件再带进去，就得到:

$X^TAX = \lambda X^TX = \lambda ||X||^2_2=\lambda$

也就是说要最大化矩阵A的二次型，就等价于找到矩阵A的最大特征值！！！

PCA降维

目标：通过数学变换，将原始的高维空间转变为一个低维空间；

给定d维空间的样本$X=[X_1,X_2,...,X_N] \in R^{dXN}$,变换之后得到$d' < d$维空间中的样本:

$$Z=[Z_1,Z_2,...,Z_N]=W^TX$$

其中$W  \in R^{dXd'}$是变换矩阵， $Z \in R^{d'XN}$是样本在新空间中的表达。我们的目标就是寻求这样的变换矩阵W$,

投影解释: $W = [W_1,W_2,...,W_{d'}]$, 为$d'$个d维向量，$Z_n = W^TX_n$, 也就是说数据样本从高维向低维空间中变换后的向量就等于转换矩阵乘以高维空间原始样本向量。

特别地，如果我们先只看一维的话，就是$W_1^TX_n$就是二者的内积！！而内积又和投影有关，我们接下来继续看PCA到底在做什么：

从上图可以看到，所谓PCA就是指样本协方差矩阵（方阵）按照特征值大小排序（因为要使得投影后数据方差最大化等价于二次型最大化等价于寻找最大特征值！），分别找到相应特征值对应的特征对象。。 

SVD理论

我们知道在PCA特征分解中是对样本数据的协方差矩阵做的，而更一般性地，对于非方阵，我们就要研究奇异值分解了。

任何$A \in R^{mXn}$的矩阵都可以分解为$A = U \sum V^T$,其中$U \in R^{mXm}, V \in R^{nXn}, \sum \in R^{mXn}$

奇异值分解SVD是特征分解的广义化，因为特征分解是对方阵来说的，而SVD奇异值分解则对任何矩阵都成立

转载于:https://www.cnblogs.com/kidsitcn/p/10384234.html