论文翻译:A Comprehensive Survey on Graph Neural Networks
论文翻译:图神经网络综合研究
arXiv:1901.00596v1
文章目录
- 论文翻译:图神经网络综合研究
- 1 引言
- 2 定义
- 3 分类和框架
- 3.1 GNN的分类
- 3.2 框架
- 4 图卷积网络
- 4.1 基于频谱的图卷积网络
- 4.1.1 背景
- 4.1.2 基于频谱的GCN方法
- 4.1.3 总结
- 4.2 基于空间法的图卷积网络
- 4.2.1 基于递归的空间GCN
- 4.2.2 基于组合的空间GCN
- 4.2.3 空间GCN的其他变体
- 4.2.4 总结
- 4.3 图池模块
- 4.4 谱模型与空间模型之间的比较
- 5 图卷积网络之外的网络
- 5.1 图注意力网络
- 5.1.1 图注意力网络方法
- 5.1.2 总结
- 5.2 图自动编码器
- 5.2.1 基于GCN的自动编码器
- 5.2.2 图自动编码器的其他变体
- 5.2.3 总结
- 5.3 图生成网络
- 5.3.1 基于GCN的图生成网络
- 5.3.2 其他图生成网络
- 5.3.3 总结
- 5.4 图时空网络
- 5.4.1 基于GCN的图时空网络
- 5.4.2 其他变体
- 5.4.3 总结
- 6 应用
- 6.1 数据集
- 6.2 基准和开源代码
- 6.3 实际应用
- 7 未来发展方向
- 结论
摘要 深度学习近年来改变了许多机器学习任务,从图像分类、视频处理到语音识别和自然语言理解等等。这些任务中的数据通常在欧几里得空间中表示。但是,越来越多的应用从非欧几里德域中生成数据,并将其表示为具有复杂关系和对象之间相互依赖性的图结构。图数据的复杂性对现有的机器学习算法提出了重大挑战。最近,出现了许多有关扩展图数据的深度学习方法的研究。在这篇综述中,我们提供了数据挖掘和机器学习领域中图神经网络(GNN)的全面概述。我们提出了一种新的分类法,将最新的图神经网络划分为不同的类别。重点关注图卷积网络,我们回顾了最近开发的新体系结构,包括图注意力网络、图自动编码器、图生成网络和图时空网络。我们将进一步讨论图神经网络在各个领域的应用,并总结现有算法在不同学习任务上的开源代码和基准。最后,我们提出了这个快速增长领域中潜在的研究方向。
关键词 深度学习,图神经网络,图卷积网络,图表示学习,图自动编码器,网络嵌入
1 引言
最新的神经网络成功推动了对模式识别和数据挖掘的研究。许多机器学习任务,例如目标检测[1]、[2],机器翻译[3]、[4]和语音识别[5],它们曾经高度依赖于手工特征工程来提取信息特征集,现在被各种端到端的深度学习优秀模型取代了,例如卷积神经网络(CNN)[6],长短期记忆(LSTM)[7]和自动编码器。深度学习在许多领域的成功部分归因于快速发展的计算资源(例如GPU)和可用的大量训练数据集,部分归因于深度学习能有效从欧几里得数据(例如图像,文本和视频)中提取潜在特征。以图像分析为例,图像可以表示为欧几里得空间中的规则网格。卷积神经网络(CNN)能够利用图像数据的平移不变性、局部连通性和图像数据的组合特性[8],因此,CNN可以提取与整个数据集共享的局部有意义特征,以进行各种图像分析任务。
尽管深度学习在欧几里得数据上取得了巨大的成功,但越来越多的应用从非欧域生成数据, 并需要对其进行有效地分析。例如,在电子商务中,基于图的学习系统能够利用用户与产品[9]、[10]、[11]之间的交互来提出高度准确推荐。在化学中,将分子建模为图数据,确定其生物活性以进行药物开发[12]、[13]。在引文网络中,论文通过引文相互链接,需要将它们分为不同的群组[14]、[15]。图数据的复杂性对现有的机器学习算法提出了重大挑战。这是因为图数据是不规则的。图可以有任意数量的无序顶点,并且图中的每个顶点具有不同数量的邻居。从而导致一些重要的操作(例如卷积)原本很容易使用在图像数据上,但不适用于图数据了。此外,现有机器学习算法的核心假设是实例彼此独立。但是,对于图数据而言,情况并非如此,其中每个实例(顶点)通过一些复杂的链接信息与其他实例(邻居)相关联,该信息能用于捕获数据之间的相互依赖性,包括引用、友谊和交互。
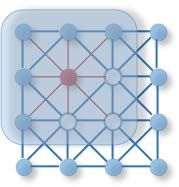
最近,人们越来越关注扩展到图数据的深度学习方法。在深度学习成功的推动下,研究人员借鉴了卷积网络、递归网络和深度自动编码器的思想,设计图神经网络的体系结构。为了处理图数据的复杂性,在过去的几年中,重要的运算操作有了新的泛化和定义。举例来说,图1说明了标准2D卷积如何启发一种图卷积。这篇综述旨在为想要进入这个快速发展领域的感兴趣的研究人员和想要比较图神经网络算法的专家提供这些方法的全面概述。
图神经网络简史 图神经网络的概念首先由[Gori et al., 2005, 16]提出,然后由[Scarselli et al., 2009, 17]进一步阐述。这些早期研究通过递归神经结构以迭代方式传播邻居信息,直到达到稳定的固定点,从而学习了目标顶点的表示。这个过程在计算上昂贵的,最近人们为克服这些挑战付出了更多的努力[18]、[19]。在我们的综述中,我们泛化了图神经网络一词,以代表图数据的所有深度学习方法。
受卷积网络在计算机视觉领域的巨大成功的启发,最近出现了许多重新定义图数据的卷积的方法,这些方法属于图卷积网络(GCN)。[Bruna et al., 2013, 20]了关于GCN的第一个重要研究,该研究基于光谱图理论开发了一种图卷积的变体。从那时起,基于频谱的图卷积网络[12]、[14]、[21]、[22]、[23]得到改进、扩展和逼近度不断提高。由于频谱方法通常同时处理整个图并且难以并行化或缩放为大型图等缺陷,因此基于空间的图卷积网络最近得到了快速发展[24]、[25]、[26]、[27]。这些方法通过汇总邻居顶点的信息直接在图域中执行卷积。连同采样策略一起,可以在一批顶点中而不是整个图形中进行计算[24]、[27],提高了效率。
除了图卷积网络以外,在过去几年中还开发了许多其他的图神经网络。这些方法包括图注意力网络,图自动编码器,图生成网络和图时空网络。这些方法的分类细节在第3节中给出。
图神经网络的相关综述 关于图神经网络的主题的现有综述数量有限。[Bronstein et al, 2017, 8]使用几何深度学习的概念,总结了非欧领域中的深度学习方法,包括图和流形。然而作为图卷积网络的第一篇评论,没有提及了几种重要的基于空间的方法,包括[15]、[19]、[24]、[26]、[27]、[28],它们成为了最先进的基准。此外,综述没有涵盖许多新开发的模型结构,这些结构对于卷积网络图同样重要。本文对这些优秀的深度学习模型进行了全面回顾,包括了图注意力网络、图自动编码器、图生成网络和图时空网络。[Battaglia et al., 29]将图网络作为从关系数据中学习的基础,在统一框架下回顾了部分图神经网络。但是,它们的通用框架是高度抽象的,失去了对原始论文中对每种方法的见识。[Lee et al., 30]对图注意力模型进行了部分总结,然图注意力模型是图神经网络的一种类型。最近,[Zhang et al., 31]发表了关于图的深度学习的最新综述,但缺少关于图生成和时空网络的研究。总而言之,现有的综述都没有提供对图神经网络的全面概述,仅涵盖了一些图卷积神经网络并提到了数量有限的文章,从而错过了其他图神经网络的最新发展,例如图生成网络和时空网络图。
图神经网络与网络嵌入 图神经网络的研究与图嵌入或网络嵌入紧密相关,另一个主题引起了数据挖掘和机器学习社区的关注[32]、[33]、[34]、[35]、[36]、[37]。网络嵌入的目的是通过保留网络拓扑结构和顶点内容信息,将网络顶点表示为低维向量空间,以便可以通过使用简单的方法轻松执行任何后续的图形分析任务,例如使用分类、聚类和推荐等现成的学习机算法(例如,用支持向量机做分类)。许多网络嵌入算法通常是无监督的算法,它们可以大致分为三类[32],即矩阵分解[38]、[39],随机游走[40]和深度学习方法。同时进行网络嵌入的深度学习方法属于图神经网络,其中包括基于图自动编码器的算法(例如DNGR[41]和SDNE[42])和无监督训练的图卷积神经网络(例如,GraphSage[24])。图2描述了网络嵌入和图神经网络之间的区别。
我们的贡献 我们的论文做出了重要贡献,总结如下:
-
新的分类法 鉴于对图数据的深度学习的研究越来越多,我们提出了一种新的图神经网络(GCN)分类法。根据这种方法,GCN分为五类:图卷积网络,图注意网络,图自动编码器,图生成网络和图时空网络。我们指出了图神经网络和网络嵌入之间的区别,并描述了不同图神经网络体系结构之间的联系。
-
全面总结 这篇综述提供了有关图数据的现代深度学习技术的最全面概述。对于每种类型的图神经网络,我们提供了有关代表性算法的详细说明,进行相应的算法的必要的比较和总结。
-
丰富的资源 这篇综述关于图神经网络提供了丰富的资源,其中包括最新的算法、基准数据集、开源代码和实际应用。这篇综述可以用作了解、使用和开发用于各种实际应用的不同深度学习方法的动手指南。
-
未来方向 这篇综述还强调了现有算法的当前局限性,并指出了这一快速发展领域中的可能方向。
文章组织 这篇综述的其余部分组织如下:第2节定义了与图相关的概念;第3部分阐明了图神经网络的分类;第4节和第5节概述了图神经网络模型;第6节介绍了各个领域的应用程序库;第7节讨论了当前的挑战并提出了未来的方向;第8节总结了论文。
2 定义
在本节中,我们提供基本图形概念的定义。为了便于检索,我们总结了表1中的常用符号。
| 符号 | 说明 |
|---|---|
| ∣ ⋅ ∣ \vert \cdot \vert ∣⋅∣ | 集合长度 |
| ⊙ \odot ⊙ | 逐点乘积 |
| A T A^T AT | 矩阵或向量 A A A的转置 |
| [ A , B ] [A,B] [A,B] | 将 A A A和 B B B拼接 |
| G \mathcal{G} G | 图 |
| V V V | 图的结点集 |
| v i v_i vi | 结点 v i ∈ V v_i \in V vi∈V |
| N ( v i ) N(v_i) N(vi) | v i v_i vi的邻居结点集 |
| E E E | 图的边集 |
| e i j e_{ij} eij | 边 e i j ∈ E e_{ij} \in E eij∈E |
| X ∈ R N × D X \in \reals^{N \times D} X∈RN×D | 图的特征矩阵 |
| x ∈ R N x \in \reals^{N} x∈RN | D = 1 D=1 D=1时图的特征向量 |
| X i ∈ R D X_i \in \reals^{D} Xi∈RD | 结点 v i v_i vi的特征向量 |
| N N N | 结点数, N = ∣ V ∣ N = \vert V \vert N=∣V∣ |
| M M M | 边数, M = ∣ E ∣ M = \vert E \vert M=∣E∣ |
| D D D | 结点的维数 |
| T T T | 时间序列中的总时长 |
定义1(图) 图 G = ( V , E , A ) \mathcal{G}=(V,E,A) G=(V,E,A)由结点集 V V V和边集 E E E构成, A A A是邻接矩阵。用 v i ∈ V v_i \in V vi∈V表示图中的一个结点,而 e i j ∈ E e_{ij} \in E eij∈E表示图中的一条边。邻接矩阵 A A A是个 N × N N \times N N×N的矩阵,如果存在 e i j ∈ E e_{ij} \in E eij∈E那么有 A i j = w i j > 0 A_{ij} = w_{ij} > 0 Aij=wij>0,反之 e i j ∉ E e_{ij} \notin E eij∈/E则 A i j = 0 A_{ij} = 0 Aij=0。顶点的度数是与其连接的边数,正式定义为 d e g r e e ( v i ) = ∑ A i , : degree(v_i) = \sum A_{i,:} degree(vi)=∑Ai,:。
图可以是由含属性 X X X的顶点链接得到,其中 X ∈ R N × D X \in \reals^{N \times D} X∈RN×D是一个特征矩阵,其中 X i ∈ R D X_i \in \reals^{D} Xi∈RD表示顶点 v i v_i vi的特征向量。在 D = 1 D = 1 D=1的情况下,我们用 x ∈ R N x \in \reals^N x∈RN代替 X X X来表示图的特征向量。
定义2(有向图) 有向图是所有边都从一个顶点指向另一个顶点的图。对于有向图, A i j ≠ A j i A_{ij} \neq A_{ji} Aij=Aji。无向图是所有边均无方向的图。对于无向图, A i j = A j i A_{ij} = A_{ji} Aij=Aji。
定义3(时空图) 时空图是特征图 X X X随时间变化。用 X ∈ R T × N × D X \in \reals^{T \times N \times D} X∈RT×N×D定义图 G = ( V , E , A , X ) \mathcal{G} = (V,E,A,X) G=(V,E,A,X),其中 T T T是时间步长。
3 分类和框架
在本节中,我们介绍了图神经网络的分类法。我们将考虑神经体系结构中任何微小差异的图神经网络模型。我们将图神经网络分为图卷积网络、图注意力网络、图自动编码器、图生成网络和图时空网络。其中,图卷积网络在获取结构依赖性方面起着核心作用。如图3所示,其他类别下的方法部分利用图卷积网络作为基础块。我们在表2中总结了每个类别中的代表方法,下面简要介绍了每个类别。
| 分类 | 论文 |
|---|---|
| GCN 基于谱方法卷积 | [12],[14],[20],[21],[22],[23],[43] |
| GCN 基于空间方法卷积 | [13],[17],[18],[19],[24],[25],[26],[27],[44],[45],[46],[47],[48],[49],[50],[51],[52],[53],[54] |
| GCN 池化方法 | [12],[21],[55],[56] |
| 图注意力网络 | [15],[28],[57],[58] |
| 图自动编码器 | [41],[42],[59],[60],[61],[62],[63] |
| 图生成网络 | [64],[65],[66],[67],[68] |
| 图时空网络 | [69],[70],[71],[72],[73] |
3.1 GNN的分类
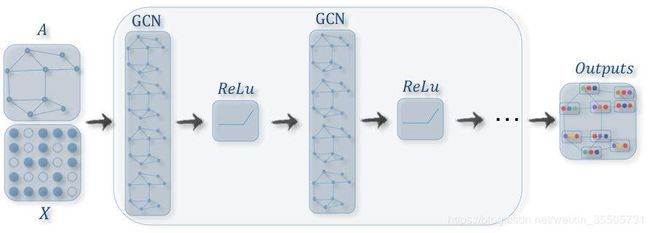
图卷积网络(GCN) 泛化了从传统数据(图像或网格)到图数据的卷积操作。GCN关键是要学习一个函数 f f f,通过聚集其自身的特征 X i X_i Xi和邻居的特征 X j X_j Xj来生成顶点 v i v_i vi的表示形式,其中 j ∈ N ( v i ) j \in N(v_i) j∈N(vi)。图4显示了用于顶点表示学习的GCN过程。图卷积网络在建立许多其他复杂的图神经网络模型(包括基于自动编码器的模型、生成模型和时空网络等)中起着核心作用。图5说明了在GCN上构建的几种图神经网络模型 。
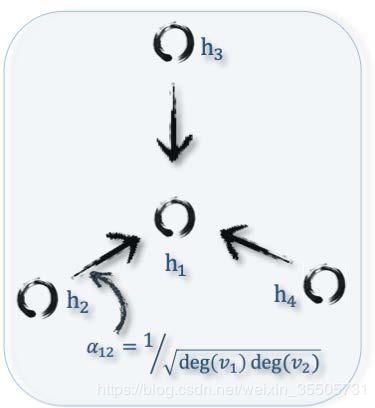
图注意力网络 类似于GCN,寻求一种聚合函数来融合图中的相邻顶点、随机游走和候选模型,以学习新的表示形式。关键区别在于图注意力网络采用注意力机制,该机制将较大的权重分配给更重要的顶点、步行或模型。注意力权重与端到端框架内的神经网络参数一起学习。图6说明了图卷积网络和图注意力网络在聚集邻居顶点信息时的区别。
图自动编码器 属于无监督的学习框架,旨在通过编码器学习低维顶点矢量,然后通过解码器重建图数据。对于没有属性信息[41]、[42]以及有属性[61]、[62]的图,图自动编码器是一种学习图嵌入的流行方法。对于普通图,许多算法通过构造具有丰富信息的新矩阵(即逐点互信息矩阵)[41],或将邻接矩阵输入自动编码器模型并捕获一阶和二阶信息[42],直接提出邻接矩阵。对于有属性图,图自动编码器模型倾向于采用GCN[14]作为编码器的构件,并通过链接预测解码器[59]、[61]重建结构信息。
图生成网络 旨在从数据生成合理的结构。从图的经验分布来看,生成图从根本上是具有挑战性的,主要是因为图是复杂的数据结构。为了解决这个问题,研究人员已探索将生成过程作为形成结点和边的因素来考虑[64]、[65],采用生成对抗训练[66]、[67]。图生成网络的一个有前途的应用领域是化合物合成。在化学图中,原子被视为顶点,化学键被视为边。任务是发现具有某些化学和物理性质的新的可合成分子。
图时空网络 旨在从时空图中学习看不见的模式,这种模式在交通预测和人类活动预测等许多应用中越来越重要。例如,基础道路交通网络是自然图,其中每个关键位置是一个其交通数据受到连续监视的顶点。通过开发有效的图时空网络模型,我们可以准确地预测整个交通系统的交通状况[70]、[71]。图时空网络的关键思想是要同时考虑空间依赖性和时间依赖性。当前的许多方法都应用GCN来捕获依赖性,并使用一些RNN[70]或CNN[71]来建模时间依赖性。
3.2 框架
图神经网络,特别是图卷积网络(GCN),通过通过图谱理论或空间局部性定义图卷积来尝试在图数据中复制CNN的成功。使用图结构和顶点内容信息作为输入,GCN的输出可以通过以下机制之一用于不同的图分析任务:
- 顶点级别的输出与顶点回归和分类任务有关。由于图卷积模块直接提供顶点的潜在表示,因此将多感知器层或softmax层用作GCN的最后一层。我们将在第4.1节和第4.2节中回顾图卷积模块。
- 边级别的输出与边分类和链接预测任务有关。为了预测边的标签/连接强度,附加函数将使用来自图形卷积模块的两个顶点的潜在表示作为输入。
- 图级别的输出与图分类任务有关。为了获得图级别的紧凑表示,池化模块用于将图粗化为子图或对顶点表示求和/求平均值。我们将在第4.3节中回顾图池模块。
| 分类 | 方法 | 输入(使用边特征?) | 输出级别 | 中间输出机制 | 最后输出机制 |
|---|---|---|---|---|---|
| 谱方法 | Spectral CNN (2014)[20] | 否 | 图级 | cluster+max pooling | softmax function |
| 谱方法 | ChebNet (2016)[12] | 否 | 图级 | efficient pooling | mlp layer+softmax function |
| 谱方法 | 1stChebNet (2017)[14] | 否 | 结点级 | activation function | softmax function |
| 谱方法 | AGCN (2018)[22] | 否 | 图级 | max pooling | sum pooling |
| 空间方法 | GNN (2009)[17] | 是 | 结点级 | - | mlp layer+softmax function |
| 空间方法 | GNN (2009)[17] | 是 | 图级 | - | add a dummy super node |
| 空间方法 | GGNNs (2015)[18] | 否 | 结点级 | - | mlp layer/softmax function |
| 空间方法 | GGNNs (2015)[18] | 否 | 图级 | - | sum pooling |
| 空间方法 | SSE (2018)[19] | 否 | 结点级 | - | softmax function |
| 空间方法 | MPNN (2017)[13] | 是 | 结点级 | - | softmax function |
| 空间方法 | MPNN (2017)[13] | 是 | 图级 | - | sum pooling |
| 空间方法 | GraphSage (2017)[24] | 否 | 结点级 | activation function | softmax function |
| 空间方法 | DCNN (2016)[44] | 是 | 结点级 | activation function | softmax function |
| 空间方法 | DCNN (2016)[44] | 是 | 图级 | - | mean pooling |
| 空间方法 | PATCHY-SAN (2016)[26] | 是 | 图级 | - | mlp layer+softmax function |
| 空间方法 | GraphSage (2017)[24] | 否 | 结点级 | skip connections | mlp layer+softmax function |
在表3中,我们列出了主要GCN方法的输入和输出的详细信息。特别是,我们总结了每个GCN层之间以及每种方法的最后一层中的输出机制。输出机制可能涉及多个合并操作,这些操作将在第4.3节中讨论。
端到端培训框架。 图卷积网络可以以(半)有监督或无监督的方式进行训练的端到端学习框架,具体取决于可用的学习任务和标签信息。
- 用于顶点级分类的半监督学习。 给定一个带有部分顶点有标记而其他顶点没标记的单个网络,图卷积网络可以学习一个健壮的模型,该模型可以有效地识别未标记顶点的类标签[14]。为此,可以通过堆叠几个图卷积层,最后添加用于多类分类的softmax层,来构建端到端框架。
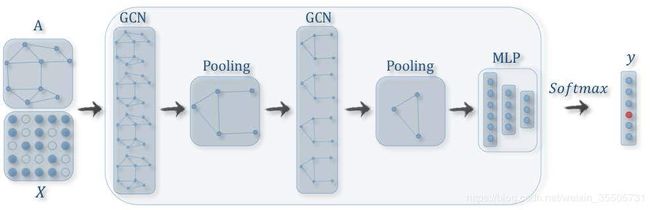
- 用于图级别分类的监督学习。 给定一个图形数据集,图形级分类旨在预测整个图形的类标签[55]、[56]、[74]、[75]。可以使用一个框架完成端到端的学习,该框架结合了图卷积层和池化过程[55]、[56]。具体来说,通过应用图卷积层,我们为每个单个图中的每个顶点获得了具有固定数量的维数的表示形式。然后,我们可以通过池化总结了图中所有顶点的表示向量获得整个图的表示。最后,通过应用现有深度学习框架中常用的MLP层和softmax层,我们可以构建用于图分类的端到端框架。在图5a中给出了一个例子。
- 图嵌入的无监督学习。 当图中没有可用的类标签时,我们可以在端到端框架中以完全无监督的方式学习图嵌入。这些算法以两种方式挖掘边级信息。一种简单的方法是采用自动编码器框架,其中编码器采用图卷积层将图嵌入到潜在表示中,在该表示中使用解码器来重构图结构[59]、[61]。另一种方法是利用负采样方法,该方法将一部分顶点对采样为负对,而图中具有链接的现有顶点对则为正对。然后在卷积层之后应用逻辑回归层进行端到端学习[24]。
4 图卷积网络
在本节中,我们将回顾图卷积网络(GCN),这是许多复杂的图神经网络模型的基础。GCN的方法分为两类,基于频谱的和基于空间的卷积。基于频谱的方法通过从图信号处理的角度引入滤波器来定义图卷积[76],其中图卷积操作被解释为从图信号中去除噪声。基于空间的方法将图卷积公式化为来自邻居的聚集特征信息。当GCN在顶点级别上运行时,图池模块可以与GCN层交错,以将图粗化为高级子结构。如图5a所示,这种体系结构设计可用于提取图级表示并执行图形分类任务。在下文中,我们分别介绍了基于频谱的GCN、基于空间的GCN和图形池模块。
4.1 基于频谱的图卷积网络
基于频谱的方法在图形信号处理中具有坚实的基础[76]。首先,我们给出了图形信号处理的一些基础知识背景,之后,我们回顾了基于谱的GCN的代表性研究。
4.1.1 背景
图的强大数学表示形式是归一化图拉普拉斯矩,定义为 L = I n − D − 1 2 A D − 1 2 L = I_n - D^{-\frac{1}{2}} A D^{-\frac{1}{2}} L=In−D−21AD−21,其中 D D D是结点的度组成的对角阵, D i i = ∑ j A i , j D_{ii} = \sum_{j} A_{i,j} Dii=∑jAi,j。归一化图拉普拉斯矩阵具有实对称正半定的性质。根据半正定的性质,归一化拉普拉斯矩阵可以分解为 L = U Λ U T L = U \Lambda U^T L=UΛUT, U = [ u ⃗ 0 , ⋯ , u ⃗ n − 1 ] ∈ R N × N U=[\vec{u}_0, \cdots, \vec{u}_{n-1}] \in \reals^{N \times N} U=[u0,⋯,un−1]∈RN×N是按特征值的排序组成的特征向量矩阵,而 Λ \Lambda Λ是特征值的对角矩阵, Λ i i = λ i i \Lambda_{ii} = \lambda_{ii} Λii=λii。归一化的拉普拉斯矩阵的特征向量形成一个正交空间,用数学术语来说, U T U = I U^T U = I UTU=I。在图信号处理中,图信号 x ⃗ ∈ R N \vec{x} \in \reals^N x∈RN是图的顶点的特征向量,其中 x ⃗ i \vec{x}_i xi是第 i i i个顶点的值。信号 x ⃗ \vec{x} x的图傅里叶变换定义为 F ( x ⃗ ) = U T x ⃗ \mathcal{F}(\vec{x}) = U^T \vec{x} F(x)=UTx,相应的图逆傅里叶变换定义为 F − 1 ( x ⃗ ^ ) = U x ⃗ ^ \mathcal{F}^{-1}(\hat{\vec{x}}) = U \hat{\vec{x}} F−1(x^)=Ux^,其中 x ⃗ ^ \hat{\vec{x}} x^表示来自图傅立叶变换的结果信号。为了理解图傅立叶变换,从其定义可以看出,它确实将输入图信号投影到正交空间,在该正交空间中,基是由归一化图拉普拉斯算子的特征向量组成。变换后的信号 x ⃗ ^ \hat{\vec{x}} x^的元素是新空间中图信号的坐标,因此输入信号可以表示为 x ⃗ = ∑ i x ⃗ ^ i u ⃗ i \vec{x} = \sum_{i} \hat{\vec{x}}_i \vec{u}_i x=∑ix^iui,这恰好是图傅立叶逆变换。现在将输入信号 x ⃗ \vec{x} x与滤波器 g ⃗ ∈ R N \vec{g} \in \reals^N g∈RN的图卷积定义为:
x ⃗ ∗ G g ⃗ = F − 1 ( F ( x ⃗ ) ⊙ F ( g ⃗ ) ) = U ( U T x ⃗ ⊙ U T g ⃗ ) (1) \begin{aligned} \vec{x} *_G \vec{g} &= \mathcal{F}^{-1} \left( \mathcal{F}(\vec{x}) \odot \mathcal{F}(\vec{g}) \right) \\ &= U \left( U^T \vec{x} \odot U^T \vec{g} \right) \end{aligned} \tag{1} x∗Gg=F−1(F(x)⊙F(g))=U(UTx⊙UTg)(1)
其中 ⊙ \odot ⊙是Hadamard积(逐点乘积)。如果定义卷积核为 g θ = d i a g ( U T g ⃗ ) g_{\theta} = diag(U^T \vec{g}) gθ=diag(UTg)(将向量对角化写成矩阵),那么图卷积可以简化为:
x ⃗ ∗ G g θ = U g θ U T x ⃗ . (2) \vec{x} *_G g_{\theta} = U g_{\theta} U^T \vec{x}. \tag{2} x∗Ggθ=UgθUTx.(2)
基于频谱的图卷积网络均遵循此定义。关键区别在于滤波器 g θ g_{\theta} gθ的选择。
4.1.2 基于频谱的GCN方法
Spectral CNN. [Bruna et al., 20]]提出了第一个谱卷积神经网络(Spectral CNN)。假设滤波器 g θ = Θ i , j k g_{\theta} = \Theta_{i,j}^k gθ=Θi,jk是一组可学习的参数,并考虑多维图信号,则它们将图卷积层定义为
X : , j k + 1 = σ ( ∑ i = 1 f k − 1 U Θ i , j k U T X : , j k ) , j = 1 , 2 , ⋯ , f k (3) X_{:,j}^{k+1} = \sigma \left( \sum_{i=1}^{f_{k-1}} U \Theta_{i,j}^k U^T X_{:,j}^{k} \right), \quad j = 1,2,\cdots, f_{k} \tag{3} X:,jk+1=σ(i=1∑fk−1UΘi,jkUTX:,jk),j=1,2,⋯,fk(3)
其中 X k ∈ R N × f k − 1 X^k \in \reals^{N \times f_{k-1}} Xk∈RN×fk−1是第 k k k层的图输入信号, N N N是结点数, f j − 1 , f k f_{j-1},f_{k} fj−1,fk分别是输入、输出的通道数。 Θ i , j k \Theta_{i,j}^k Θi,jk是对角线元素为可学习参数决定的对角阵, σ ( . ) \sigma(.) σ(.)是非线性激活函数。
Chebyshev Spectral CNN (ChebNet). [Defferrard et al., 12]提出将滤波器定义为特征值对角矩阵的Chebyshev多项式的ChebNet, g θ = ∑ k = 0 K θ k T k ( Λ ~ ) , Λ ~ = 2 Λ λ m a x − I N g_{\theta} = \sum_{k=0}^{K} \theta_k T_{k} (\tilde{\Lambda}), \tilde{\Lambda} = \frac{2 \Lambda}{\lambda_{max}} - I_{N} gθ=∑k=0KθkTk(Λ~),Λ~=λmax2Λ−IN。Chebyshev多项式由递归定义为 T k ( x ) = 2 x T k − 1 ( x ) − T k − 2 ( x ) T_k(x) = 2xT_{k-1}(x) - T_{k-2}(x) Tk(x)=2xTk−1(x)−Tk−2(x),另外 T 0 ( x ) = 1 , T 1 ( x ) = x T_0(x)=1,T_1(x)=x T0(x)=1,T1(x)=x。因此,图形信号 x ⃗ \vec{x} x与定义的滤波器 g θ g_{\theta} gθ的卷积为:
x ⃗ ∗ G g θ = U ( ∑ k = 0 K θ k T k ( Λ ~ ) ) U T x ⃗ = ∑ k = 0 K θ k T k ( L ~ ) x ⃗ (4) \begin{aligned} \vec{x} *_G g_{\theta} &= U \left( \sum_{k=0}^{K} \theta_k T_{k} (\tilde{\Lambda}) \right) U^T \vec{x} \\ &= \sum_{k=0}^{K} \theta_k T_{k} (\tilde{L}) \vec{x} \end{aligned} \tag{4} x∗Ggθ=U(k=0∑KθkTk(Λ~))UTx=k=0∑KθkTk(L~)x(4)
其中 L ~ = 2 L λ m a x − I N \tilde{L} = \frac{2 L}{\lambda_{max}} - I_{N} L~=λmax2L−IN。
根据等式(4),ChebNet隐式避免了图傅立叶基 U U U的计算,从而将计算复杂度从 O ( N 3 ) \mathcal{O}(N^3) O(N3)降低到 O ( K M ) \mathcal{O}(KM) O(KM)。由于 T k ( L ~ ) T_{k} (\tilde{L}) Tk(L~)是第 k k k阶 L ~ \tilde{L} L~的多项式,因此 T k ( L ~ ) x ⃗ T_{k} (\tilde{L}) \vec{x} Tk(L~)x在每个顶点上经行局部操作。因此,ChebNet的卷积核作于局部空间上。
First order of ChebNet (1stChebNet) [Kipf et al., 14]介绍了ChebNet的一阶近似。令 K = 1 , λ m a x = 2 K = 1, \lambda_{max} = 2 K=1,λmax=2,等式(4)简化为:
x ⃗ ∗ G g θ = θ 0 T 0 ( L ~ ) x ⃗ + θ 1 T 1 ( L ~ ) x ⃗ = θ 0 x ⃗ + θ 1 L ~ x ⃗ = θ 0 x ⃗ + θ 1 ( 2 L λ m a x − I N ) x ⃗ = θ 0 x ⃗ + θ 1 ( I N − D − 1 2 A D − 1 2 − I N ) x ⃗ = θ 0 x ⃗ − θ 1 D − 1 2 A D − 1 2 x ⃗ . (5) \begin{aligned} \vec{x} *_G g_{\theta} &= \theta_0 T_0(\tilde{L}) \vec{x} + \theta_1 T_1(\tilde{L}) \vec{x} \\ &= \theta_0 \vec{x} + \theta_1 \tilde{L} \vec{x} \\ &= \theta_0 \vec{x} + \theta_1 \left( \frac{2 L}{\lambda_{max}} - I_{N} \right) \vec{x} \\ &= \theta_0 \vec{x} + \theta_1 \left( I_N - D^{-\frac{1}{2}} A D^{-\frac{1}{2}} - I_{N} \right) \vec{x} \\ &= \theta_0 \vec{x} - \theta_1 D^{-\frac{1}{2}} A D^{-\frac{1}{2}} \vec{x}. \end{aligned} \tag{5} x∗Ggθ=θ0T0(L~)x+θ1T1(L~)x=θ0x+θ1L~x=θ0x+θ1(λmax2L−IN)x=θ0x+θ1(IN−D−21AD−21−IN)x=θ0x−θ1D−21AD−21x.(5)
为了限制参数的数量并避免过度拟合,1stChebNet进一步 θ = θ 0 = − θ 1 \theta = \theta_0 = -\theta_1 θ=θ0=−θ1,从而得出以下图卷积的定义:
x ⃗ ∗ G g θ = θ ( I N + D − 1 2 A D − 1 2 ) x ⃗ . (6) \vec{x} *_G g_{\theta} = \theta \left( I_N + D^{-\frac{1}{2}} A D^{-\frac{1}{2}} \right) \vec{x}. \tag{6} x∗Ggθ=θ(IN+D−21AD−21)x.(6)
为了合并多维图输入信号,修改公式(6),1stChebNet提出了一个图形卷积层:
X k + 1 = A ~ X k Θ (7) X^{k+1} = \tilde{A} X^k \Theta \tag{7} Xk+1=A~XkΘ(7)
其中 A ~ = I N + D − 1 2 A D − 1 2 \tilde{A} = I_N + D^{-\frac{1}{2}} A D^{-\frac{1}{2}} A~=IN+D−21AD−21。
Renormalization Trick 原文[Kipf et al., 14]中使用了renormalization trick,做出了一些修改:
I N + D − 1 2 A D − 1 2 → D ~ − 1 2 A ~ D ~ − 1 2 . I_N + D^{-\frac{1}{2}} A D^{-\frac{1}{2}} \rightarrow \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}. IN+D−21AD−21→D~−21A~D~−21.
其中 A ~ = A + I N , D ~ i , i = ∑ j A ~ i , j \tilde{A}=A+I_N,\tilde{D}_{i,i} = \sum_{j}\tilde{A}_{i,j} A~=A+IN,D~i,i=∑jA~i,j。
输入 X ∈ R N × f k X \in \mathbb{R}^{N \times f_{k}} X∈RN×fk,经过滤波 Θ ∈ R f k × f k + 1 \Theta \in \mathbb{R}^{f_{k} \times f_{k+1}} Θ∈Rfk×fk+1得到含有 F F F个通道的卷积后结果 Z ∈ R N × f k + 1 Z \in \mathbb{R}^{N \times f_{k+1}} Z∈RN×fk+1:
X k + 1 = ( D ~ − 1 2 A ~ D ~ − 1 2 ) X k Θ = ( ( D + I N ) − 1 2 ( A + I N ) ( D + I N ) − 1 2 ) X k Θ = △ A ^ X k Θ . \begin{aligned} X^{k+1} &= \left( \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} \right) X^k \Theta \\ &= \left( (D + I_N)^{-\frac{1}{2}} (A + I_N) (D + I_N)^{-\frac{1}{2}} \right) X^k \Theta \\ &\overset{\triangle}{=} \hat{A} X^k \Theta. \end{aligned} Xk+1=(D~−21A~D~−21)XkΘ=((D+IN)−21(A+IN)(D+IN)−21)XkΘ=△A^XkΘ.
由1stChebNet定义的图卷积具有空间局部性。它弥合了基于频谱的方法与基于空间的方法之间的差距。输出的每一行代表每个顶点的潜在表示,这些隐含表示是通过以 A ~ \tilde{A} A~行指定的权重对来自顶点本身及其相邻顶点的聚合信息进行线性变换而获得的。但是,1stChebNet的主要缺点是,在批处理训练期间,计算成本随着1stChebNet层数的增加而呈指数增长。后一层中的每个顶点都必须递归地扩展其先前层之间的邻域。[Chen et al., 45]假设等式(7)中重新缩放的相邻矩阵 A ~ \tilde{A} A~来自某抽样分布。在此假设下,使用Monte Carlo和方差减少技术来简化训练过程。[Chen et al., 46]通过对邻域进行采样并使用历史隐藏表示,将图卷积的接收域大小减小到任意小比例。[Huang et al., 54]提出了一种自适应的分层采样方法来加速1stChebNet的训练,其中较低层的采样以顶层为条件。该方法也适用于显式方差减少。
Adaptive Graph Convolution Network (AGCN). 为了探索图拉普拉斯矩阵未指定的隐藏结构关系,[Li et al., 22]提出了自适应图卷积网络(AGCN)。AGCN用所谓的残差图扩充图,该残差图是通过计算顶点的成对距离而构造的。尽管能够捕获互补关系信息,但是AGCN仍需要进行昂贵的 O ( N 2 ) \mathcal{O}(N^2) O(N2)计算复杂度。
4.1.3 总结
频谱CNN[20]依赖于拉普拉斯矩阵的特征分解。它具有三个影响:首先,对图的任何扰动都会导致特征根的变化;其次,学习的过滤器是域相关的,这意味着它们不能应用于具有不同结构的图;第三,特征值分解需要 O ( N 3 ) \mathcal{O}(N^3) O(N3)计算和 O ( N 2 ) \mathcal{O}(N^2) O(N2)内存。由ChebNet[12]和1stChebNet[14]定义的卷积核具有空间局部性。可以在图中的不同位置共享学习的权重。但是,频谱方法的一个常见缺点是它们需要将整个图形加载到内存中以执行图形卷积,这在处理大图形时效率不高。
4.2 基于空间法的图卷积网络
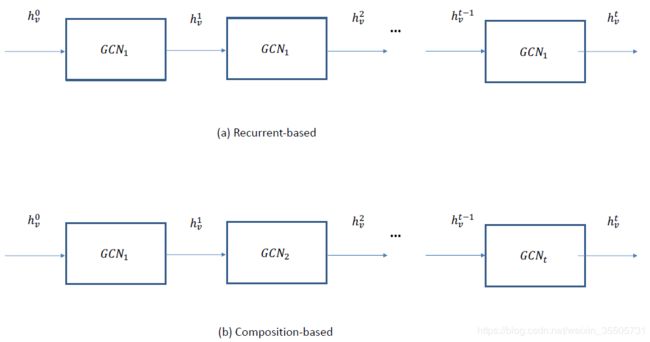
基于空间的方法模仿了图像上常规卷积神经网络的卷积操作,基于顶点的空间关系定义了图卷积。为了将图像与图相关联,可以将图像视为图的一种特殊形式,每个像素代表一个结点。如图1a所示,每个像素都直接连接到其附近的像素。对于 3 × 3 3 \times 3 3×3窗口,每个顶点的邻域是其周围的八个像素。这八个像素的位置表示顶点邻居的顺序。然后,通过获取每个通道上中心顶点及其邻居的像素值的加权平均值,将滤波器应用于 3 × 3 3 \times 3 3×3块上。由于相邻顶点的特定排序,可训练权重能够在不同位置之间共享。类似地,对于一般图,基于空间的图卷积采用中心顶点表示及其邻居表示的聚合来获得该顶点的新表示,如图1b所示。为了探究顶点接收场的深度和广度,通常的做法是将多个图卷积层堆叠在一起。根据堆叠卷积层的不同方法,基于空间的GCN可以进一步分为两类,基于递归的GCN和基于组合的GCN。基于递归的方法应用相同的图卷积层来更新隐藏的表示,而基于组合的方法应用不同的图卷积层来更新隐藏的表示。图7说明了这种差异。下面,我们概述这两个分支。
4.2.1 基于递归的空间GCN
基于递归的方法的主要思想是递归更新顶点的潜在表示,直到达到稳定的固定点为止。这是通过对递归函数施加约束[17],采用门递归单元架构[18],异步和随机地更新顶点潜在表示[19]来完成的。下面,我们将介绍这三种方法。
Graph Neural Networks(GNNs) 作为图神经网络上最早的作品之一,GNN递归地更新顶点潜在表示,直到收敛为止。换句话说,从扩散过程的角度来看,每个顶点都与其邻居交换信息,直到达到平衡为止。为了处理异构图,GNN的空间图卷积定义为
h ⃗ v t = f ( l ⃗ v , l ⃗ c o [ v ] , h ⃗ n e t − 1 [ v ] , l ⃗ n e [ v ] ) (8) \vec{h}_{v}^{t} = f\left(\vec{l}_{v}, \vec{l}_{co}[v], \vec{h}_{ne}^{t-1}[v], \vec{l}_{ne}[v] \right) \tag{8} hvt=f(lv,lco[v],hnet−1[v],lne[v])(8)
其中 l ⃗ v \vec{l}_{v} lv表示顶点 v v v的标签属性, l ⃗ c o [ v ] \vec{l}_{co}[v] lco[v]表示顶点 v v v的相应边的标签属性, h ⃗ n e t [ v ] \vec{h}_{ne}^{t}[v] hnet[v]表示在时间步 t t t处顶点 v v v的邻居的隐藏表示, l ⃗ n e [ v ] \vec{l}_{ne}[v] lne[v]表示顶点 v v v的邻居的标签属性。
为了确保收敛,递归函数 f ( . ) f(.) f(.)必须是压缩映射,这会在映射后缩小两点之间的距离。如果 f ( . ) f(.) f(.)是神经网络,则必须对参数的雅可比矩阵施加惩罚项。GNN使用Almeida-Pineda算法[77]、[78]训练其模型。核心思想是运行传播过程以到达固定点,然后在给出收敛解的情况下执行反向过程。
Gated Graph Neural Networks (GGNNs) GGNN使用门控循环单元(GRU)[79]作为循环函数,将循环减少到固定数量的步骤。GGNN的空间图卷积定义为
h ⃗ v t = G R U ( h ⃗ v t − 1 , ∑ u ∈ N ( v ) W h ⃗ u t ) (9) \vec{h}_{v}^{t} = GRU \left(\vec{h}_{v}^{t-1}, \sum_{u \in \mathcal{N}(v)} W \vec{h}_{u}^{t} \right) \tag{9} hvt=GRU⎝⎛hvt−1,u∈N(v)∑Whut⎠⎞(9)
与GNN不同,GGNN使用时间反向传播(BPTT)来学习参数。优势在于,它不再需要约束参数来确保收敛。但是,BPTT训练的缺点是牺牲了时间和记忆效率。对于大型图而言,这尤其成问题,因为GGNN需要在所有顶点上多次运行递归函数,从而需要将所有顶点的中间状态存储在内存中。
Stochastic Steady-state Embedding (SSE). 为了提高学习效率,SSE算法[19]以异步方式随机更新顶点潜在表示。如算法1所示,SSE递归估计顶点潜在表示并使用采样的批处理数据更新参数。为了确保收敛到稳态,SSE的递归函数定义为历史状态和新状态的加权平均值,
h ⃗ v t = ( 1 − α ) h ⃗ v t − 1 + α W 1 σ ( W 2 [ x ⃗ v , ∑ u ∈ N ( v ) [ h ⃗ u t , x ⃗ u ] ] ) (10) \vec{h}_{v}^{t} = (1 - \alpha) \vec{h}_{v}^{t-1} + \alpha W_1 \sigma \left(W_2 \left[ \vec{x}_v, \sum_{u \in \mathcal{N}(v)}[\vec{h}_{u}^{t}, \vec{x}_u ] \right] \right) \tag{10} hvt=(1−α)hvt−1+αW1σ⎝⎛W2⎣⎡xv,u∈N(v)∑[hut,xu]⎦⎤⎠⎞(10)
尽管求邻域信息和隐含地考虑了顶点度,但是求和的规模是否影响该算法的稳定性仍然值得怀疑。
4.2.2 基于组合的空间GCN
基于组合的方法通过堆叠多个图卷积层来更新顶点的表示形式。
Message Passing Neural Networks (MPNNs). [Gilmer et al., 13]将几种现有的图卷积网络(包括[12]、[14]、[18]、[20]、[53]、[80]、[81])归纳为一个称为消息传递神经网络(MPNN)的统一框架。MPNN由两个阶段组成,即消息传递阶段和读取阶段。消息传递阶段实际上运行 T T T步基于空间的图卷积。图卷积运算通过消息函数 M t ( . ) M_t(.) Mt(.)和更新函数 U t ( . ) U_t(.) Ut(.)根据
h ⃗ v t = U t ( h ⃗ v t − 1 , ∑ u ∈ N ( v ) M t ( h ⃗ v t − 1 , h ⃗ u t − 1 , e ⃗ v u ) ) . (11) \vec{h}_{v}^{t} = U_t \left( \vec{h}_{v}^{t-1}, \sum_{u \in \mathcal{N}(v)} M_t (\vec{h}_{v}^{t-1}, \vec{h}_{u}^{t-1}, \vec{e}_{vu} ) \right). \tag{11} hvt=Ut⎝⎛hvt−1,u∈N(v)∑Mt(hvt−1,hut−1,evu)⎠⎞.(11)
读出阶段实际上是一个池化操作,该池化操作基于每个单独顶点的隐藏表示来生成整个图的表示。定义为
y ⃗ ^ = R ( h ⃗ v T ∣ v ∈ G ) . (12) \hat{\vec{y}} = R(\vec{h}_v^T | v \in \mathcal{G}). \tag{12} y^=R(hvT∣v∈G).(12)
通过输出函数 R ( . ) R(.) R(.),最终表示 y ⃗ ^ \hat{\vec{y}} y^用于执行图级预测任务。作者介绍了通过假设 U t ( . ) U_t(.) Ut(.)和 M t ( . ) M_t(.) Mt(.)的不同形式,其他几个图卷积网络也落入了它们的框架。
GraphSage[24] 引入了聚合函数的概念来定义图卷积。聚合功能实质上是收集顶点的邻居信息。它必须对顶点顺序(例如均值、求和和最大函数)的排列保持不变。图卷积运算定义为
h ⃗ v t = σ ( W t agg k ( h ⃗ t t − 1 , { h ⃗ u t − 1 , ∀ u ∈ N ( v ) } ) ) (13) \vec{h}_v^t = \sigma \left( W^t \text{agg}_k \left( \vec{h}_t^{t-1}, \{ \vec{h}_u^{t-1}, \forall u \in \mathcal{N}(v) \} \right) \right) \tag{13} hvt=σ(Wtaggk(htt−1,{hut−1,∀u∈N(v)}))(13)
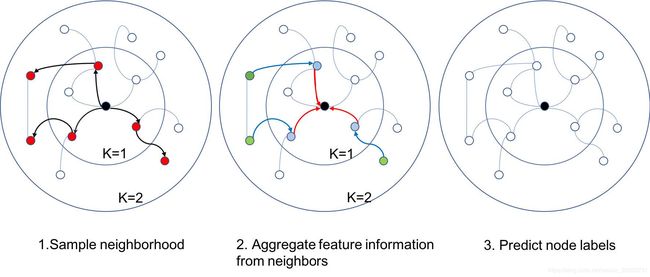
GraphSage提出了一种批量训练算法,而不是更新所有顶点上的状态,该算法提高了大型图的可伸缩性。GraphSage的学习过程包括三个步骤。首先,它以固定大小对顶点的本地k-hop邻域进行采样。其次,它通过汇总其邻居特征信息来得出中心顶点的最终状态。最后,它使用中心顶点的最终状态进行预测和反向传播错误。此过程如图8所示。
假设在第 t t t跳处要采样的邻居数为 s t s_t st,则GraphSage在同一批次中的时间复杂度为 O ( ∏ t = 1 T s t ) \mathcal{O}\left( \prod_{t=1}^{T} s_t \right) O(∏t=1Tst)。因此,计算成本随着 t t t的增加呈指数增长。这样可以防止GraphSage具有较深的体系结构。但是,实际上,作者发现在 t = 2 t = 2 t=2的情况下,GraphSage已经实现了高性能。
4.2.3 空间GCN的其他变体
Diffusion Convolution Neural Networks (DCNN)[44] 提出了一种图卷积网络,该网络封装了图扩散过程。通过将输入与转移概率矩阵的幂级数独立卷积,可以得到隐藏顶点表示。DCNN的扩散卷积运算公式为:
Z i , j , : m = f ( W j , : ⊙ P i , j , : m X i , : m ) . (14) Z_{i,j,:}^{m} = f \left( W_{j,:} \odot P_{i,j,:}^{m} X_{i,:}^{m} \right). \tag{14} Zi,j,:m=f(Wj,:⊙Pi,j,:mXi,:m).(14)
在公式(14)中, Z i , j , : m Z_{i,j,:}^{m} Zi,j,:m表示图 m m m中 j j j-hop的的隐藏表示, P : , j , : m P_{:,j,:}^{m} P:,j,:m表示图 m m m中的 j j j-hop的概率转移矩阵, X i , : m X_{i,:}^{m} Xi,:m表示图 m m m中的顶点 i i i的输入特征。其中 Z m ∈ R N m × H × F Z^m \in \reals^{N_m \times H \times F} Zm∈RNm×H×F, W ∈ R H × F W \in \reals^{H \times F} W∈RH×F, P m ∈ R N m × H × N m P^m \in \reals^{N_m \times H \times N_m} Pm∈RNm×H×Nm, X m ∈ R N m × F X^m \in \reals^{N_m \times F} Xm∈RNm×F。
尽管DCNN模型通过更高阶的过渡矩阵拥有较大的接收域,但仍需要 O ( N m 2 H ) \mathcal{O}(N_m^2 H) O(Nm2H)内存,将其应用于大型图时会导致严重问题。
PATCHY-SAN[26] 使用标准卷积神经网络(CNN)解决图分类任务。为此,它将图形结构的数据转换为网格结构的数据。首先,它使用图形标注过程为每个图选择固定数量的顶点。图标记过程实质上是为图中的每个顶点分配一个等级,该等级可以基于顶点度、中心性、Weisfeiler-Lehman颜色[82]、[83]等。第二,图中的每个顶点可以具有不同数量的邻居,PATCHY-SAN根据每个顶点的图标签排序选择固定数量的邻居。最后,在形成固定大小的网格结构数据之后,PATCHYSAN使用标准的CNN来学习图形隐藏表示。在GCN中使用标准CNN具有保持移位不变的优势,而后者依赖于排序功能。结果,顶点选择和排序过程中的排名标准至关重要。在PATCHY-SAN中,排名基于图标签。但是,图标签仅考虑图结构,而忽略顶点特征信息。
Large-scale Graph Convolution Networks (LGCN). 在后续工作中,大型图卷积网络(LGCN)[27]提出了一种基于顶点特征信息的排序方法。与PATCHY-SAN不同,LGCN使用标准CNN生成顶点级输出。对于每个顶点,LGCN都会组合其邻域的特征矩阵,并沿每一列对该特征矩阵进行排序。排序后的特征矩阵的前 k k k行被用作目标顶点的输入网格数据。最后,LGCN将一维CNN应用于结果输入,以获得目标顶点的隐藏表示。虽然在PATCHYSAN中派生图形标签需要复杂的预处理,但LGCN中的特征值排序不需要预处理步骤,因此效率更高。为了适应大型图的情况,LGCN提出了一种子图训练策略,该策略将采样的子图放入一个小批量中。
Mixture Model Network (MoNet)[25] 将标准CNN与非欧几里德域上的卷积架构统一起来。虽然几种基于空间的方法在聚合邻域特征信息时会忽略顶点与其邻居之间的相对位置,但MoNet引入了伪坐标和权重函数,以使顶点邻居的权重由顶点与其邻居之间的相对位置(伪坐标)确定。在这样的框架下,关于流形的多种方法,例如测地线CNN(GCNN)[84],各向异性CNN(ACNN)[85],样条CNN[86],以及诸如GCN[14],DCNN[44]等图都可以被概括为MoNet的特殊实例。但是,这些方法在MoNet框架下具有固定权重功能。MoNet提出了一个具有可学习参数的高斯核,以自由调整权重函数。
4.2.4 总结
基于空间的方法通过聚集来自邻居的特征信息来定义图卷积。根据堆叠图卷积层的不同方式,基于空间的方法分为基于递归的和基于组合的两类。虽然基于递归的方法尝试获取顶点的稳态,但是基于组合的方法尝试合并更高阶的邻域信息。在每一层中,两组都必须在训练期间更新所有顶点上的隐藏状态。但是,它效率很低,因为它必须将所有中间状态存储到内存中。为了解决这个问题,已经提出了几种训练策略,包括用于基于组合的方法(例如GraphSage[24])的子图训练以及用于基于循环的方法(例如SSE[19])的随机异步训练。
4.3 图池模块
当将卷积神经网络推广到图结构数据时,另一个关键组件,图池模块也至关重要,特别是对于图级分类任务[55]、[56]、[87]。据[Xu et al., 88],池辅助GCN在区分图结构方面与Weisfeiler-Lehman检验[82]一样强大。类似于CNN附带的原始池化层,图池化模块可以通过对原始特征数据进行下采样来轻松减少方差和计算复杂性。平均值/最大值/求和池化是实现此目的的最原始、最有效的方法,因为在池化窗口中计算平均值/最大值/求和值很快。
h ⃗ G = mean/max/sum ( h ⃗ 1 T , ⋯ , h ⃗ n T ) (15) \vec{h}_{\mathcal{G}} = \text{mean/max/sum}(\vec{h}_{1}^T, \cdots, \vec{h}_{n}^T) \tag{15} hG=mean/max/sum(h1T,⋯,hnT)(15)
[Henaff et al., 21]证明,在网络开始时执行简单的最大/均值合并对于降低图域的维数和减轻昂贵的图傅立叶变换操作的成本尤为重要。
[Defferrard et al., 12]优化了最大/最小池,并在其方法ChebNet中为设备提供了一种有效的池化策略。输入图首先通过图5a中描述的粗化处理进行处理。粗化后,输入图的顶点及其粗化版本将在平衡的二叉树中重新形成。在最粗糙的级别上任意排序顶点,然后在平衡的二叉树中将此排序传播到更低的级别,最终将在最高级上产生规则的排序。合并这种重新排列的1D信号比原始信号效率更高。
[Zhang et al., 55]提出了一种框架DGCNN,该框架具有类似的名为SortPooling的池化策略,该策略通过将顶点重新排列为有意义的顺序来执行池化。与ChebNet[12]不同,DGCNN根据顶点在图中的结构作用对顶点进行排序。来自空间图卷积的图的无序顶点特征被视为连续的WL颜色[82],然后将它们用于对顶点进行排序。除了对顶点特征进行排序外,它还可以通过截断/扩展图形的特征张量来将图形大小统一为 k k k。如果 n > k n > k n>k,则删除最后的 n − k n-k n−k行,否则添加 k − n k-n k−n个零行。此方法通过解决图结构化任务背后的一个挑战(称为置换不变)来增强池网络,以提高GCN的性能。Verma和Zhang提出了图囊网络[89],该网络进一步探索了图数据的置换不变性。
最近,提出了一个池化模块DIFFPOOL[56],它可以生成图的分层表示,并且不仅可以与CNN结合,还可以以端到端的方式与各种图神经网络架构结合。与所有以前的粗化方法相比,DIFFPOOL不仅可以将一个图中的顶点进行聚类,而且还可以提供一种通用的解决方案,以便在一组广泛的输入图中对顶点进行分层池化。这是通过在第 1 1 1层学习一个称为群集分配矩阵 S ( l ) ∈ R n l × n l + 1 S^{(l)} \in \reals^{n_l \times n_l + 1} S(l)∈Rnl×nl+1来完成的。具有输入群集顶点特征 X ( l ) X^{(l)} X(l)和粗化的邻接矩阵 A ( l ) A^{(l)} A(l)的两个单独的GNN被用来生成分配矩阵 S ( l ) S^{(l)} S(l)和嵌入矩阵 Z ( l ) Z^{(l)} Z(l)如下:
Z ( l ) = G N N l , e m b e d ( A ( l ) , X ( l ) ) S ( l ) = softmax ( G N N l , p o o l ( A ( l ) , X ( l ) ) ) (17) \begin{aligned} Z^{(l)} &= GNN_{l,embed}(A^{(l)}, X^{(l)}) \\ S^{(l)} &= \text{softmax}\left( GNN_{l,pool}(A^{(l)}, X^{(l)}) \right) \end{aligned} \tag{17} Z(l)S(l)=GNNl,embed(A(l),X(l))=softmax(GNNl,pool(A(l),X(l)))(17)
公式(16)和(17)可以用任何标准GNN模块来实现,该模块处理相同的输入数据,但参数却不同,因为它们在框架中所扮演的角色是不同的。 G N N l , e m b e d GNN_{l,embed} GNNl,embed嵌入将产生新的嵌入,而 G N N l , p o o l GNN_{l,pool} GNNl,pool生成输入顶点到 n l + 1 n_{l + 1} nl+1个簇的概率分配。在式(17)中以行方式应用Softmax函数。结果, S ( l ) S^{(l)} S(l)的每一行对应于层 1 1 1的 n l n_l nl个顶点(或群集)之一,而 S ( l ) S^{(l)} S(l)的每一列对应到下一层的 n l n_l nl之一。一旦有了 Z ( l ) Z^{(l)} Z(l)和 S ( l ) S^{(l)} S(l),合并操作如下:
X ( l + 1 ) = ( S ( l ) ) T Z ( l ) ∈ R n l + 1 × d A ( l + 1 ) = ( S ( l ) ) T A ( l ) S ( l ) ∈ R n l + 1 × n l + 1 (19) \begin{aligned} X^{(l+1)} &= (S^{(l)})^T Z^{(l)} \in \reals^{n_{l+1} \times d} \\ A^{(l+1)} &= (S^{(l)})^T A^{(l)} S^{(l)} \in \reals^{n_{l+1} \times n_{l+1}} \end{aligned} \tag{19} X(l+1)A(l+1)=(S(l))TZ(l)∈Rnl+1×d=(S(l))TA(l)S(l)∈Rnl+1×nl+1(19)
等式(18)采用聚类嵌入 Z ( l ) Z^{(l)} Z(l),然后根据聚类分配 S ( l ) S^{(l)} S(l)对这些嵌入进行聚合,以计算 n l + 1 n_{l+1} nl+1个聚类中的每一个的嵌入。最初的群集嵌入将是顶点表示。类似地,等式(19)将邻接矩阵 A ( l ) A^{(l)} A(l)作为输入,并生成表示每个集群对之间的连通性强度的粗化邻接矩阵。总体而言,DIFFPOOL[56]通过使用两个GNN对顶点进行聚类来重新定义了图形池模块。任何标准的GCN模块都可以与DIFFPOOL结合使用,不仅可以实现增强的性能,而且可以加快卷积操作。
4.4 谱模型与空间模型之间的比较
作为最早的图形数据卷积网络,基于频谱的模型在许多图形相关的分析任务中均取得了令人印象深刻的结果。这些模型之所以吸引人,是因为它们在图形信号处理方面具有理论基础。通过设计新的图形信号滤波器[23],我们可以在理论上设计新的图形卷积网络。但是,基于频谱的模型有几个缺点。下面我们从效率、泛化性和灵活性三个方面说明这一点。
在效率方面,基于频谱的模型的计算成本随着图的大小而急剧增加,因为它们要么需要特征向量计算[20],要么同时处理整个图,这使得它们难以并行或缩放到大图。基于空间的模型具有处理大型图的潜力,因为它们通过聚集邻居顶点直接在图域中执行卷积。可以在一批顶点而不是整个图中执行计算。当相邻顶点的数量增加时,可以开发采样技术[24]、[27]以提高效率。
在泛化性方面,基于频谱的模型假设有固定的图,这使得它们很难推广到新的图或不同的图。另一方面,基于空间的模型在每个顶点上本地执行图卷积,可以在不同位置和结构之间轻松共享权重。
在灵活性方面,基于频谱的模型仅限于在无向图上使用。在有向图上没有明确的拉普拉斯矩阵定义,因此将基于频谱的模型应用于有向图的唯一方法是将有向图转换为无向图。基于空间的模型更灵活地处理诸如边缘特征和边缘方向之类的多源输入,因为这些输入可以合并到聚合函数中(例如[13]、[17]、[51]、[52]、[ 53])。
结果,空间模型近年来引起了越来越多的关注[25]。
5 图卷积网络之外的网络
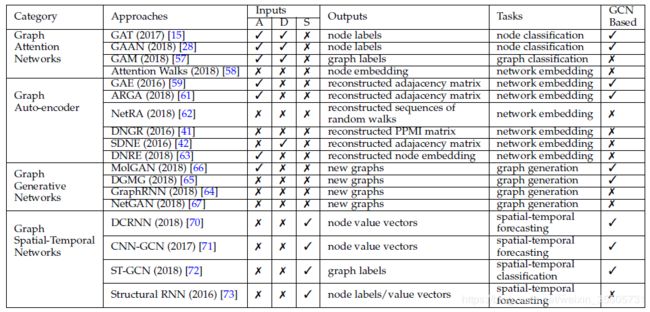
在本节中,我们将回顾其他图神经网络,包括图注意力神经网络、图自动编码器、图生成网络和图时空网络。在表4中,我们总结了每个类别下的主要方法。
5.1 图注意力网络
注意机制几乎已经成为基于序列的任务的标准[90]。注意机制的优点是它们专注于对象最重要部分的能力。该专业已被证明可用于许多任务,例如机器翻译和自然语言理解。由于注意力机制的模型容量增加,图神经网络还可以通过在聚合过程中使用注意力,集成多个模型的输出以及生成面向重要性的随机游走而从中受益。在本节中,我们将讨论在图结构化数据中如何使用注意力机制。
5.1.1 图注意力网络方法
Graph Attention Network (GAT)[15] 是一个基于空间的图卷积网络,在聚合特征信息时,注意力机制涉及确定顶点邻居的权重。GAT的图卷积运算定义为
h ⃗ i t = σ ( ∑ j ∈ N i α ( h ⃗ i t − 1 , h ⃗ j t − 1 ) W t − 1 h ⃗ j t − 1 ) (20) \vec{h}_{i}^{t} = \sigma \left( \sum_{j \in \mathcal{N}_i} \alpha \left( \vec{h}_{i}^{t-1}, \vec{h}_{j}^{t-1} \right) W^{t-1} \vec{h}_{j}^{t-1} \right) \tag{20} hit=σ⎝⎛j∈Ni∑α(hit−1,hjt−1)Wt−1hjt−1⎠⎞(20)
其中 α ( . ) \alpha(.) α(.)是注意函数,它自适应地控制邻居 j j j对顶点 i i i的贡献。为了学习不同子空间中的注意力权重,GAT使用多头注意力。
h ⃗ i t = ∥ k = 1 K σ ( ∑ j ∈ N i α k ( h ⃗ i t − 1 , h ⃗ j t − 1 ) W k t − 1 h ⃗ j t − 1 ) (21) \vec{h}_{i}^{t} = \|_{k=1}^{K} \sigma \left( \sum_{j \in \mathcal{N}_i} \alpha_k \left( \vec{h}_{i}^{t-1}, \vec{h}_{j}^{t-1} \right) W_k^{t-1} \vec{h}_{j}^{t-1} \right) \tag{21} hit=∥k=1Kσ⎝⎛j∈Ni∑αk(hit−1,hjt−1)Wkt−1hjt−1⎠⎞(21)
其中 ∥ \| ∥是拼接操作。
Gated Attention Network (GAAN)[28] 还采用多头注意力关注机制来更新顶点的隐藏状态。但是,GAAN并没有为每个头部分配相等的权重,而是引入了一种自我关注机制,该机制会为每个头部计算不同的权重。更新规则定义为:
h ⃗ i t = ϕ o ( x ⃗ i ⊕ ∥ k = 1 K g i k ∑ j ∈ N i α k ( h ⃗ i t − 1 , h ⃗ j t − 1 ) ϕ v ( h ⃗ j t − 1 ) ) (22) \vec{h}_{i}^{t} = \phi_o \left( \vec{x}_i \oplus \|_{k=1}^{K} g_i^k \sum_{j \in \mathcal{N}_i} \alpha_k \left( \vec{h}_{i}^{t-1}, \vec{h}_{j}^{t-1} \right) \phi_v (\vec{h}_{j}^{t-1}) \right) \tag{22} hit=ϕo⎝⎛xi⊕∥k=1Kgikj∈Ni∑αk(hit−1,hjt−1)ϕv(hjt−1)⎠⎞(22)
其中 ϕ 0 ( . ) , ϕ v ( . ) \phi_0(.),\phi_v(.) ϕ0(.),ϕv(.)表示前馈神经网络,而 g i k g_i^k gik是第 k k k注意力头的注意力权重。
Graph Attention Model (GAM)[57] 提出了一种递归神经网络模型来解决图分类问题,该模型通过自适应地访问一系列重要顶点来处理图的信息部分。GAM模型定义为
h ⃗ t = f ⃗ h ( f ⃗ s ( r ⃗ t − 1 , v t − 1 , g ; θ s ) , h ⃗ t − 1 ; θ h ) (23) \vec{h}_t = \vec{f}_h \left( \vec{f}_s \left( \vec{r}_{t-1}, v_{t-1}, g;\theta_s \right), \vec{h}_{t-1}; \theta_h \right) \tag{23} ht=fh(fs(rt−1,vt−1,g;θs),ht−1;θh)(23)
其中 f ⃗ h ( . ) \vec{f}_h(.) fh(.)是LSTM网络, f ⃗ s ( . ) \vec{f}_s(.) fs(.)是从当前顶点 v t − 1 v_{t-1} vt−1到其邻居 c ⃗ t \vec{c}_t ct迈出一步的步阶网络,优先考虑那些类型由策略生成的 v t − 1 v_{t-1} vt−1中具有较高等级的顶点网络:
r ⃗ t = f r ( h ⃗ t ; θ r ) (24) \vec{r}_t = f_r(\vec{h}_t; \theta_r) \tag{24} rt=fr(ht;θr)(24)
其中 r ⃗ t \vec{r}_t rt是一个随机序向量,它指示哪个顶点更重要,因此应进行更高优先级的进一步研究, h ⃗ t \vec{h}_t ht包含代理商通过对图的探索而聚集的历史信息,并用于对图标签进行预测。
Attention Walks[58] 通过随机游走来学习顶点嵌入。与使用固定先验的DeepWalk[40]不同,“注意步行”将具有不同注意权重的共现矩阵分解。
E [ D ] = P ~ ( 0 ) ∑ k = 1 C a k ( P ) k (25) \mathbb{E}[D] = \tilde{P}^{(0)} \sum_{k=1}^{C} a_k (P)^k \tag{25} E[D]=P~(0)k=1∑Cak(P)k(25)
其中 D D D表示共生矩阵, P ~ ( 0 ) \tilde{P}^{(0)} P~(0)表示初始位置矩阵, P P P表示概率转移矩阵。
5.1.2 总结
注意机制通过三种不同的方式对图神经网络做出贡献,即在聚集特征信息时将注意权重分配给不同的邻居,根据注意权重组装多个模型,以及使用注意权重来指导随机游走。尽管将GAT[15]和GAAN[28]归类在图注意力网络下,但它们也可以同时被视为基于空间的图卷积网络。GAT[15]和GAAN[28]的优势在于,它们可以适应性地学习邻居的重要性权重,如图6所示。但是,由于必须计算每对邻居之间的注意力权重,计算成本和内存消耗迅速增加。
5.2 图自动编码器
图自动编码器是一类网络嵌入方法,旨在通过使用神经网络体系结构将网络顶点表示为低维向量空间。一种典型的解决方案是利用多层感知器作为编码器来获取顶点嵌入,其中解码器重建顶点的邻域统计信息,例如正点互信息(PPMI)[41]或第一和第二阶邻近度[42]。最近,研究人员在设计图形自动编码器时,探索了将GCN[14]用作编码器,将GCN[14]与GAN[91]组合,或将LSTM[7]与GAN[91]组合使用。我们将首先回顾基于GCN的自动编码器,然后总结该类别中的其他变体。
5.2.1 基于GCN的自动编码器
Graph Auto-encoder (GAE)[59] 首先将GCN[14]集成到图自动编码器框架中。编码器定义为
Z = G C N ( X , A ) (26) Z = GCN(X,A) \tag{26} Z=GCN(X,A)(26)
解码器定义为:
A ^ = σ ( Z Z T ) (27) \hat{A} = \sigma(Z Z^T) \tag{27} A^=σ(ZZT)(27)
GAE的框架也显示在图5b中。GAE可以以变化的方式进行训练,即最小化变化的下限 L L L:
L = E q ( Z ∣ X , A ) [ log p ( A ∣ Z ) ] − K L [ q ( Z ∣ X , A ) ∥ p ( Z ) ] (28) L = \mathbb{E}_{q(Z|X,A)} \left[ \log_p(A|Z) \right] - KL \left[ q(Z|X,A) \| p(Z)\right] \tag{28} L=Eq(Z∣X,A)[logp(A∣Z)]−KL[q(Z∣X,A)∥p(Z)](28)
Adversarially Regularized Graph Autoencoder (ARGA)[61] 采用生成对抗网络(GAN)的训练方案[91]来规范化图自动编码器。在ARGA中,编码器将顶点的结构信息及其特征编码为GCN[14]的隐藏表示,然后解码器从编码器的输出中重建邻接矩阵。GAN在生成模型的训练中,在生成器和判别器之间玩最小-最大游戏。生成器会生成尽可能真实的“伪造样本”,而判别器会尽力将“伪造样本”与真实样本区分开。GAN帮助ARGA规范学习到的顶点的隐藏表示形式,以遵循先前的分布。详细地,编码器充当生成器,试图使学习到的顶点隐藏的表示与真实的先验分布难以区分。另一方面,判别器试图识别学习的顶点隐藏表示是从编码器生成还是从实际的先验分布生成。
5.2.2 图自动编码器的其他变体
Network Representations with Adversarially Regularized Autoencoders (NetRA)[62] 是一个图自动编码器框架,与ARGA有相似的想法。它还通过对抗训练对顶点隐藏表示进行规范化,使其符合先前的分布。他们没有重建邻接矩阵,而是恢复了通过序列到序列体系结构从随机游走中采样的顶点序列[92]。
Deep Neural Networks for Graph Representations (DNGR)[41] 用堆叠式去噪自动编码器[93]来重构逐点互信息矩阵(PPMI)。当图通过随机游走序列化为序列时,PPMI矩阵本质上捕获顶点共现信息。正式地,PPMI矩阵定义为
P P M I v 1 , v 2 = max ( log ( c o u n t ( v 1 , v 2 ) ∣ D ∣ c o u n t ( v 1 ) c o u n t ( v 2 ) ) , 0 ) (29) PPMI_{v_1,v_2} = \max \left( \log \left( \frac{count(v_1,v_2)|D|}{count(v_1)count(v_2)} \right), 0 \right) \tag{29} PPMIv1,v2=max(log(count(v1)count(v2)count(v1,v2)∣D∣),0)(29)
其中 ∣ D ∣ = ∑ v 1 , v 2 c o u n t ( v 1 , v 2 ) , v 1 , v 2 ∈ V |D| = \sum_{v_1,v_2} count(v_1,v_2), v_1,v_2 \in V ∣D∣=∑v1,v2count(v1,v2),v1,v2∈V。堆叠式去噪自动编码器能够学习数据背后的高度非线性规律。与传统的神经自动编码器不同,它通过将输入项随机切换为零来增加输入噪声。学习得到的潜在表示更加鲁棒,特别是当存在缺失值时。
Structural Deep Network Embedding (SDNE)[42] 使用堆叠式自动编码器共同保留顶点的一阶接近度和二阶接近度。一阶邻近度定义为顶点的隐藏表示形式与其邻居的隐藏表示形式之间的距离。一阶接近度的目标是使相邻顶点的表示尽可能彼此靠近。具体而言,损失函数 L 1 s t L_{1st} L1st定义为
L 1 s t = ∑ i , j = 1 n A i , j ∥ h ⃗ i ( k ) − h ⃗ j ( k ) ∥ 2 (30) L_{1st} = \sum_{i,j=1}^{n} A_{i,j} \| \vec{h}_i^{(k)} - \vec{h}_j^{(k)} \|^2 \tag{30} L1st=i,j=1∑nAi,j∥hi(k)−hj(k)∥2(30)
二阶接近度定义为顶点输入与其重构输入之间的距离,其中输入是顶点在相邻矩阵中的对应行。二阶邻近度的目标是保留顶点的邻域信息。具体而言,损失函数 L 2 n d L_{2nd} L2nd定义为
L 2 n d = ∑ i = 1 n ∥ ( x ⃗ ^ i − x ⃗ i ) ⊙ b ⃗ i ∥ 2 (31) L_{2nd} = \sum_{i=1}^{n} \| (\hat{\vec{x}}_i - \vec{x}_i) \odot \vec{b}_i \|^2 \tag{31} L2nd=i=1∑n∥(x^i−xi)⊙bi∥2(31)
向量 b ⃗ i \vec{b}_i bi的作用是惩罚非零元素,因为输入非常稀疏。详细地,如果 A i , j = 0 A_{i,j}=0 Ai,j=0则 b i , j = 1 b_{i,j}=1 bi,j=1,如果 A i , j = 1 A_{i,j}=1 Ai,j=1,则 b i , j = β > 1 b_{i,j}=\beta > 1 bi,j=β>1。总的来说,目标函数定义为
L = L 2 n d + α L 1 s t + λ L r e g (32) L = L_{2nd} + \alpha L_{1st} + \lambda L_{reg} \tag{32} L=L2nd+αL1st+λLreg(32)
其中 L r e g L_{reg} Lreg是 L 2 L_2 L2范式惩罚项。
深度递归网络嵌入(DRNE)[63] 直接重建顶点的隐藏状态,而不是整个图统计信息。通过使用聚合函数作为编码器,DRNE将损耗函数设计为:
L = ∑ v ∈ V ∥ h ⃗ v − agg ( h ⃗ u ∣ u ∈ N ( v ) ) ∥ 2 (33) L = \sum_{v \in V} \| \vec{h}_v - \text{agg} (\vec{h}_u | u \in \mathcal{N}(v)) \|^2 \tag{33} L=v∈V∑∥hv−agg(hu∣u∈N(v))∥2(33)
DRONE的一项创新是它选择LSTM作为聚合函数,其中邻居序列按其顶点程度排序。
5.2.3 总结
DNGR和SDNE仅在给出拓扑结构的情况下学习顶点嵌入,而GAE、ARGA、NetRA、DRNE在拓扑信息和顶点内容特征均可用时学习顶点嵌入。图自动编码器的一个挑战是邻接矩阵A的稀疏性,导致解码器的正项数量远远少于负项。为解决此问题,DNGR重建了一个更密集的矩阵,即PPMI矩阵,SDNE对邻接矩阵的零项施加了惩罚,GAE对邻接矩阵中的项进行了加权,并且NetRA将图线性化为序列。
5.3 图生成网络
图生成网络的目标是给定一组观察到的图来生成图。图生成网络的许多方法都是有特定于领域的。例如,在分子图生成中,一些模型对称为SMILES[94]、[95]、[96]、[97]的分子图的字符串表示建模。在自然语言处理中,通常以给定的句子为条件来生成语义图或知识图[98]、[99]。最近,已经提出了几种通用方法。一些工作将生成过程作为顶点和边的交替形成因素[64]、[65],而另一些工作则采用生成对抗训练[66]、[67]。此类别中的方法或者将GCN用作构建块,或者使用不同的体系结构。
5.3.1 基于GCN的图生成网络
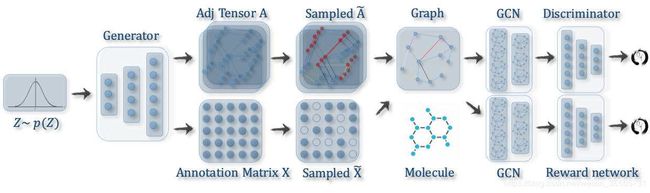
Molecular Generative Adversarial Networks (MolGAN)[66] 集成了GCN[100],改进的GAN[101]和强化学习(RL),以生成具有所需属性的图形。GAN由生成器和判别器组成,它们相互对抗以提高生成器的真实性。在MolGAN中,生成器尝试提出伪造的图及其特征矩阵,而判别器的目的是从经验数据中区分伪造的样本。另外,与判别器并行引入了奖励网络,以根据外部评估者鼓励生成的图具有某些属性。MolGAN的框架如图9所示。
Deep Generative Models of Graphs (DGMG)[65] 利用基于空间的图卷积网络来获取现有图的隐藏表示。生成顶点和边的决策过程以结果图表示为条件。简而言之,DGMG递归地为不断增长的图提出一个顶点,直到触发停止条件。在添加新顶点后的每个步骤中,DGMG反复决定是否在添加的顶点上添加边,直到该决定变为否。如果该决定为真,则它将评估将新添加的顶点连接到所有现有顶点的概率分布,并从该概率分布中采样一个顶点。将新顶点及其连接添加到现有图后,DGMG再次更新图表示。
5.3.2 其他图生成网络
GraphRNN[64] 通过两级递归神经网络利用深图生成模型。图级RNN每次都向顶点序列添加一个新顶点,而边缘级RNN生成一个二进制序列,该序列指示新添加的顶点与序列中先前生成的顶点之间的连接。为了将图线性化为顶点序列以训练图级别RNN,GraphRNN采用广度优先搜索(BFS)策略。为了建模用于训练边缘级RNN的二进制序列,GraphRNN假定多元伯努利或条件伯努利分布。
NetGAN[67] 将LSTM[7]与Wasserstein GAN[102]结合使用,可以从基于随机游走的ap方法生成图形。GAN框架包含两个模块,一个生成器和一个判别器。生成器尽最大努力通过LSTM网络生成合理的随机游动,而判别器则试图将伪随机游动与真实随机游动区分开。训练后,通过对出现在一组随机游走中的顶点的共现矩阵进行归一化,来获得新的图。
5.3.3 总结
评估生成的图仍然是一个难题。与可以由人类专家直接评估的合成图像或音频不同,生成的图形的质量很难通过视觉检查。MolGAN和DGMG利用外部知识来评估生成的分子图的有效性。GraphRNN和NetGAN通过图形统计信息(例如顶点度)评估生成的图形。DGMG和GraphRNN依次生成顶点和边,而MolGAN和NetGAN联合生成顶点和边。根据[68],前一种方法的缺点是当图变大时,对长序列建模是不现实的。后一种方法的挑战在于,图形的全局属性难以控制。最近的一种方法[68]采用变分自动编码器通过提出邻接矩阵,施加惩罚项来解决有效性约束来生成图。但是,由于具有 n n n个顶点的图的输出空间为 n 2 n^2 n2,因此这些方法都无法扩展到大型图。
5.4 图时空网络
图时空网络同时捕获时空图的空间和时间相关性。时空图具有全局图结构,每个顶点的输入随时间变化。例如,在交通网络中,作为顶点的每个传感器连续记录某条道路的交通速度,其中交通网络的边缘由传感器对之间的距离确定。图时空网络的目标可以是预测未来的顶点值或标签,或预测时空图标签。最近的研究已经探索了单独使用GCN[72],将GCN与RNN[70]或CNN[71]结合使用,以及为图结构量身定制的循环架构[73]。在下面,我们介绍这些方法。
5.4.1 基于GCN的图时空网络
Diffusion Convolutional Recurrent Neural Network (DCRNN)[70] 引入扩散卷积作为图卷积以捕获空间依赖性,并使用具有门控循环单元(GRU)[79]的序列到序列体系结构[92]来捕获时间依赖性。
扩散卷积模拟具有向前和向后方向的截断扩散过程。 形式上,定义扩散卷积
X : , p ⋆ G f ( θ ) = ∑ k = 0 K − 1 [ θ k 1 ( D O − 1 A ) k + θ k 2 ( D I − 1 A T ) k ] X : , p (34) X_{:,p} \star_G f(\theta) = \sum_{k=0}^{K-1} \left[ \theta_{k1} \left( D_{O}^{-1} A \right)^k + \theta_{k2} \left( D_{I}^{-1} A^T \right)^k \right] X_{:,p} \tag{34} X:,p⋆Gf(θ)=k=0∑K−1[θk1(DO−1A)k+θk2(DI−1AT)k]X:,p(34)
其中 D O D_{O} DO是出度矩阵,而 D I D_{I} DI是入度矩阵。为了允许多个输入和输出通道,DCRNN提出了一个扩散卷积层,定义为
Z : , q = σ ( ∑ p = 1 P X : , p ⋆ G f ( Θ q , p , : , : ) ) (35) Z_{:,q} = \sigma \left( \sum_{p=1}^{P} X_{:,p} \star_G f(\Theta_{q,p,:,:}) \right) \tag{35} Z:,q=σ(p=1∑PX:,p⋆Gf(Θq,p,:,:))(35)
其中 X ∈ R N × P , Z ∈ R N × Q , Θ ∈ R Q × P × K × 2 X \in \reals^{N \times P}, Z \in \reals^{N \times Q}, \Theta \in \reals^{Q \times P \times K \times 2} X∈RN×P,Z∈RN×Q,Θ∈RQ×P×K×2。 Q Q Q是输出通道数, P P P是输入通道数。
为了捕获时间依赖性,DCRNN使用扩散卷积层处理GRU的输入,以便循环单元同时接收来自上一时间步长的历史信息和来自图卷积的邻域信息。 DCRNN中修改后的GRU称为扩散卷积门控递归单元(DCGRU),
r ⃗ ( t ) = sigmoid ( Θ r ⋆ G [ X ( t ) , H ( t − 1 ) ] + b ⃗ r ) u ⃗ ( t ) = sigmoid ( Θ u ⋆ G [ X ( t ) , H ( t − 1 ) ] + b ⃗ u ) C ( t ) = tanh ( Θ C ⋆ G [ X ( t ) , ( r ⃗ ( t ) ⊙ H ( t − 1 ) ) ] + b ⃗ r ) H ( t ) = u ⃗ ( t ) ⊙ H ( t − 1 ) + ( 1 − u ⃗ ( t ) ) ⊙ C ( t ) (36) \begin{aligned} \vec{r}^{(t)} &= \text{sigmoid} \left( \Theta_r \star_G \left[ X^{(t)}, H^{(t-1)} \right] + \vec{b}_r \right) \\ \vec{u}^{(t)} &= \text{sigmoid} \left( \Theta_u \star_G \left[ X^{(t)}, H^{(t-1)} \right] + \vec{b}_u \right) \\ C^{(t)} &= \text{tanh} \left( \Theta_C \star_G \left[ X^{(t)}, ( \vec{r}^{(t)} \odot H^{(t-1)}) \right] + \vec{b}_r \right) \\ H^{(t)} &= \vec{u}^{(t)} \odot H^{(t-1)} + (1 - \vec{u}^{(t)}) \odot C^{(t)} \end{aligned} \tag{36} r(t)u(t)C(t)H(t)=sigmoid(Θr⋆G[X(t),H(t−1)]+br)=sigmoid(Θu⋆G[X(t),H(t−1)]+bu)=tanh(ΘC⋆G[X(t),(r(t)⊙H(t−1))]+br)=u(t)⊙H(t−1)+(1−u(t))⊙C(t)(36)
为了满足多步预测的需求,DCGRN采用了序列到序列的体系结构[92],其中递归单元被DCGRU取代。
CNN-GCN[71] 交错使用GCN的1D-CNN[14]来学习时空图数据。 对于输入张量 X ∈ R T × N × D X \in \reals^{T \times N \times D} X∈RT×N×D,一维CNN层沿时间轴在 X [ : , i , : ] X_{[:,i,:]} X[:,i,:]上滑动,以汇总每个顶点的时间信息,而GCN层在 X [ i , : , : ] X_{[i,:,:]} X[i,:,:]汇总每个时间步的空间信息。 输出层是线性变换,为每个顶点生成预测。 CNN-GCN的框架如图5c所示。
Spatial Temporal GCN (ST-GCN)[72] 通过将时间流扩展为图的边缘来采用不同的方法,以便可以使用统一的GCN模型同时提取空间和时间信息。 ST-GCN定义了一种标注功能,可以根据两个相关顶点的距离为图的每个边缘分配一个标注。 这样,邻接矩阵可以表示为 K K K个邻接矩阵的总和,其中 K K K是标记的数量。 然后,ST-GCN将具有不同权重矩阵的GCN [14]应用于每个K邻接矩阵并求和。
f ⃗ o u t = ∑ j Λ j − 1 2 A j Λ j − 1 2 f ⃗ i n W j . (37) \vec{f}_{out} = \sum_j \Lambda_{j}^{ -\frac{1}{2} } A_j \Lambda_{j}^{ -\frac{1}{2} } \vec{f}_{in} W_j. \tag{37} fout=j∑Λj−21AjΛj−21finWj.(37)
5.4.2 其他变体
Structural-RNN. [Jain et al., 73] 提出了一个循环结构框架,称为Structural-RNN。 Structural-RNN的目的是在每个时间步预测顶点标签。 在Structured-RNN中,它由两种RNN组成,即nodeRNN和edgeRNN。 每个顶点和每个边缘的时间信息分别通过nodeRNN和edgeRNN。 由于为不同的顶点和边缘假设不同的RNN会极大地增加模型的复杂性,因此它们将顶点和边缘分为语义组。 例如,人对对象交互图由两组顶点(人为顶点和对象顶点)以及三组边,人对人边缘,对象对对象边缘和人对对象边缘组成。 同一语义组中的顶点或边共享相同的RNN模型。 为了合并空间信息,nodeRNN将把edgeRNN的输出作为输入。
5.4.3 总结
DCRNN的优点是由于循环网络架构的缘故,它能够处理长期依赖关系。 尽管比DCRNN更简单,但由于快速实施一维CNN,CNN-GCN可以更有效地处理时空图。 ST-GCN将时间流视为图的边缘,从而导致邻接矩阵的大小呈平方增长。 一方面,这增加了图卷积层的计算成本。 另一方面,为了捕获长期依赖关系,图卷积层必须堆叠多次。 结构化RNN通过在同一语义组内共享同一RNN来提高模型效率。 但是,Structure-RNN需要人类先验知识来拆分语义组。
6 应用
图神经网络具有广泛的应用。 在本节中,我们首先总结文献中经常使用的基准数据集。 然后,我们报告四个常用数据集的基准性能,并列出图神经网络的可用开源实现。 最后,我们提供了图神经网络在各个领域中的实际应用。
6.1 数据集
在我们的调查中,我们计算了在本工作回顾的论文中出现的每个数据集的频率,并在表5中报告了至少出现两次的数据集。
Citation Networks 包括论文,作者及其之间的关系,例如引文,作者身份,合著者。尽管引文网络是有向图,但在评估顶点分类,链接预测和顶点聚类任务的模型性能时,它们通常被视为无向图。有三种流行的论文引用网络数据集:Cora,Citeseer和Pubmed。 Cora数据集包含2708个机器学习出版物,分为七个类别。 Citeseer数据集包含3327篇科学论文,分为六类。 Cora和Citeseer中的每篇论文都用一个热向量表示,该向量指示字典中是否存在单词。 Pubmed数据集包含19717个与糖尿病有关的出版物。 Pubmed中的每篇论文都由术语“频率反文档频率”(TF-IDF)向量表示。此外,DBLP是一个大型的引文数据集,包含从计算机科学书目中收集的数百万篇论文和作者。可以在 https://dblp.uni-trier.de 上找到DBLP的原始数据集。 https://aminer.org/citation 不断更新DBLP论文引文网络的处理版本。
Social Networks 是由来自在线服务(例如BlogCatalog,Reddit和Epinions)的用户交互形成的。 BlogCatalog数据集是一个由博客作者及其社交关系组成的社交网络。 博客作者的标签代表他们的个人兴趣。 Reddit数据集是由从Reddit讨论论坛收集的帖子形成的无向图。 如果两个帖子包含同一用户的评论,则将链接两个帖子。 每个帖子都有一个标签,指示其所属的社区。 Epinions数据集是从在线产品评论网站收集的多重关系图,评论者可以在其中拥有多种类型的关系,例如信任、不信任、共同审阅和共同评估。
Chemical/Biological Graphs 化学分子和化合物可以用化学图表示,原子为顶点,化学键为边。此类图通常用于评估图分类性能。 NCI-1和NCI-9数据集分别包含4100和4127种化学化合物,标记它们是否具有活性以阻止人类癌细胞系的生长。 MUTAG数据集包含188种硝基化合物,标明它们是芳香族还是杂芳香族。 D&D数据集包含1178个蛋白质结构,并标明了它们是酶还是非酶。 QM9数据集包含以13个化学特性标记的133885个分子。 Tox21数据集包含标记有12种毒性的12707种化学化合物。另一个重要的数据集是蛋白质-蛋白质相互作用网络(PPI)。它包含24个生物学图,其中顶点由蛋白质表示,边缘由蛋白质之间的相互作用表示。在PPI中,每个图都与人体组织相关联。每个顶点都标有其生物学状态。
Unstructured Graphs 为了测试图神经网络对非结构化数据的泛化,k最近邻图(k-NN图)已被广泛使用。 MNIST数据集包含70000张大小为28×28的图像,并用10位数字标记。 将MNIST图像转换为图形的典型方法是根据其像素位置构造8-NN图形。 Wikipedia数据集是从Wikipedia转储的前一百万个字节中提取的单词共现网络。 词的标签表示词性(POS)标签。 20-NewsGroup数据集包含大约20,000个按20种新闻类型分类的新闻组(NG)文本文档。 通过将每个文档表示为一个顶点,并使用顶点之间的相似性作为边缘权重来构造20-NewsGroup的图形。
Others 还有其他几个数据集值得一提。 METR-LA是从洛杉矶县高速公路收集的交通数据集。 来自MovieLens网站的MovieLens-1M数据集包含6k用户给出的100万个项目评分。 它是推荐系统的基准数据集。 NELL数据集是从永无止境的语言学习项目获得的知识图。 它由包含三个实体及其关系的三元组表示的事实组成。
6.2 基准和开源代码
在表5列出的数据集中,Cora,Pubmed,Citeseer和PPI是最常用的数据集。他们经常经过测试以比较图卷积网络在顶点分类任务中的性能。在表6中,我们报告了这四个数据集的基准性能,所有这些数据集均使用标准数据拆分。开源实现促进了深度学习研究中基线实验的工作。由于存在大量的超参数,因此不使用已发布的代码就很难获得与文献中报道的结果相同的结果。在表7中,我们提供了第4-5节中回顾的图神经网络模型的开源实现的超链接。值得注意的是,Fey等。 [86]在PyTorch中发布了一个名为PyTorch Geometric的几何学习库,该库实现了包含ChebNet[12],1stChebNet[14],GraphSage[24],MPNN[13],GAT[15]和SplineCN[86]N的服务器图神经网络。最近,发布了深度图库(DGL),在许多流行的深度学习平台(例如PyTorch和MXNet)之上提供了一组功能丰富的图神经网络的快速实现。
6.3 实际应用
图神经网络在不同的任务和领域中具有广泛的应用。 尽管GNN的每个类别都有专门的常规任务,包括顶点分类、顶点表示学习、图分类、图生成和时空预测,但GNN还可用于顶点聚类,链接预测[119]、和图分区[120]。 在本节中,我们主要根据它们所属的一般领域介绍实际应用。
Computer Vision 图神经网络的最大应用领域之一是计算机视觉。 研究人员对在场景图生成、点云分类和分割、动作识别以及许多其他方向上利用图结构。
在场景图生成中,对象之间的语义关系有助于理解视觉场景背后的语义。 给定图像,场景图生成模型检测并识别对象,并预测对象对之间的语义关系[121]、[122]、[123]。 另一个应用通过给定场景图生成逼真的图像来逆转该过程[124]。 由于自然语言可以解析为语义图,其中每个单词代表一个对象,因此对于给定文本描述的图像合成方法是一种很有前途的解决方案。
在点云分类和分割中,点云是由LiDAR扫描记录的一组3D点。 这项任务的解决方案使LiDAR设备能够看到周围的环境,这通常对无人驾驶车辆有利。 为了识别点云所描绘的对象,[125]、[126]、[127]将点云转换为k最近邻图或超点图,并使用图卷积网络探索拓扑结构。
在动作识别中,识别视频中包含的人类动作有助于从机器方面更好地理解视频内容。 一组解决方案可检测视频剪辑中人体关节的位置。 由骨骼链接的人体关节自然会形成图形。 给定人类关节位置的时间序列,[72]、[73]应用时空神经网络来学习人类的行为模式。
此外,在计算机视觉中应用图神经网络的可能方向的数量仍在增长。 这包括少拍图像分类[128]、[129],语义分割[130]、[131],视觉推理[132]和问题解答[133]。
Recommender Systems 基于图的推荐系统将项目和用户作为顶点。 通过利用项目与项目之间,用户与用户之间,用户与项目之间以及内容信息之间的关系,基于图的推荐系统可以生成高质量的建议。 推荐系统的关键是为用户打分商品的重要性。 结果,可以将其视为链接预测问题。 目的是预测用户和项目之间缺少的链接。 为了解决这个问题,[Van et al., 9]和[Ying et al., 11]。 提出了一种基于GCN的图形自动编码器。 [Monti et al., 10]结合GCN和RNN来学习生成已知评级的基本过程。
Traffic 交通拥堵已成为现代城市的热门社会问题。在路线规划和流量控制中,准确预测交通网络中的交通速度,交通量或道路密度至关重要。 [28]、[70]、[71]、[134]采用具有时空神经网络的基于图的方法。他们模型的输入是一个时空图。在该时空图中,顶点由放置在道路上的传感器表示,边由成对顶点在阈值以上的距离表示,并且每个顶点都包含一个时间序列作为特征。目标是预测时间间隔内道路的平均速度。另一个有趣的应用是出租车需求预测。这极大地帮助了智能交通系统利用资源并有效地节约能源。鉴于历史出租车需求,位置信息,天气数据和事件特征,[Yao et al., 135]结合LSTM,CNN和由LINE[136]训练的顶点嵌入,以形成每个位置的联合表示,以预测某个时间间隔内某个位置所需的出租车的数量。
Chemistry 在化学领域,研究人员应用图神经网络来研究分子的图结构。 在分子图中,原子起顶点作用,化学键起边作用。 顶点分类、图分类和图生成是针对分子图的三个主要任务,目的是学习分子指纹[53]、[80],预测分子特性[13],推断蛋白质界面[137]以及合成化学物质[65]、[66]、[138]。
Others 对于将GNN应用到其他问题,例如程序验证[18]、程序推理[139]、社会影响预测[140]、对抗性攻击预防[141]、电气健康记录模型[142]、[143]、事件检测[144]和组合优化[145]已有初步探索。
7 未来发展方向
尽管图神经网络已经证明了其在学习图数据中的能力,但是由于图的复杂性,仍然存在挑战。 在本节中,我们提供了图神经网络的四个未来方向。
Go Deep 深度学习的成功在于深度神经网络架构。 例如,在图像分类中,名为ResNet[146]的杰出模型具有152层。 然而,关于图形,实验研究表明,随着层数的增加,模型的性能会急剧下降[147]。 根据[147],这是由于图卷积的影响,因为它实质上将相邻顶点的表示推向彼此更近的位置,因此,从理论上讲,在无限次卷积的情况下,所有顶点的表示都将收敛到单个点。 这就提出了一个问题,即深入学习是否仍然是学习图结构数据的好策略。
Receptive Field 顶点的接受域是指包括中心顶点及其邻居的一组顶点。 顶点的邻居数遵循幂律分布。 一些顶点可能只有一个邻居,而其他顶点可能邻居多达数千个。 尽管已经采用了采样策略[24]、[26]、[27],但是如何选择顶点的代表性接收场仍有待探索。
Scalability 对于大型图,大多数图神经网络不能很好地缩放。 造成这种情况的主要原因是,当堆叠图卷积的多层时,顶点的最终状态涉及其邻居的大量隐藏状态,从而导致反向传播的高度复杂性。 虽然几种方法试图通过快速采样[45]、[46]和子图训练[24]、[27]来提高其模型效率,但它们仍不足以扩展以处理具有大图的深度架构。
Dynamics and Heterogeneity 当前的大多数图神经网络都处理静态齐次图。 一方面,假定图结构是固定的。 另一方面,假定图中的顶点和边来自单个来源。 但是,这两个假设在许多情况下都不现实。 在社交网络中,新人可以随时进入网络,而现有人也可以退出网络。 在推荐系统中,产品可能具有不同的类型,其中产品的输入可能具有不同的形式,例如文本或图像。 因此,应开发新的方法来处理动态和异构图结构。
结论
在这项综述中,我们对图神经网络进行了全面的概述。 我们提供了一个分类法,将图神经网络分为五类:图卷积网络、图注意力网络、图自动编码器和图生成网络。 我们对类别内或类别间的方法进行了全面的回顾,比较和总结。 然后,我们介绍图神经网络的广泛应用。 总结了图神经网络的数据集,开源代码和基准。 最后,我们提出了图神经网络的四个未来方向。