整理的apollo 入门课程

转载自：https://mp.csdn.net/postedit/81081744

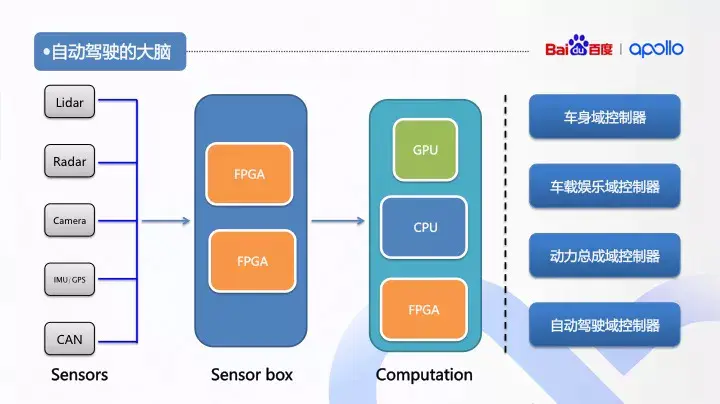
自动驾驶系统主要包含三个部分：感知、决策、控制。从整个硬件的架构上也要充分考虑系统感知、决策、控制的功能要求。自动驾驶硬件包括：1.自动驾驶系统的硬件架构2.自动驾驶的传感器3.自动驾驶传感器的产品定义4.自动驾驶的大脑5.自动驾驶汽车的线控系统

无人驾驶主要包括5部分：计算机视觉、传感器融合、定位、路径规划、控制

开放式软件层包括：实时操作系统、运行时框架和应用程序模块层。

ubuntu+apollo内核=RTOS

apollo用protobuf接口语言代替了ros消息，解决消息兼容性问题

apollo云服务包含：高精度地图、仿真环境平台、数据平台、安全、空中软件升级、DuerOS智能语音系统

apollo提供的数据包括交通灯数据、包围盒数据、语义分割数据。已经发布了apolloscape数据集。

 

 

高精度地图

所谓的高精地图包含大量驾驶辅助信息，包括道路网的三维表征，例如交叉路口和路标位置

还包含很多语义信息，比如，交通灯不同颜色的含义

定位、感知和规划软件依赖于高精度地图，高精度地图可帮助车辆找到合适的行车空间，可以帮助规划起确定不同的路线选择，并帮助预测，利用高精度地图可以使车辆精良靠近中心行驶

Apollo 高精地图的道路元素定义

标准 OpenDRIVE v.s. Apollo OpenDRIVE

主要区别	标准 OpenDRIVE	Apollo OpenDRIVE
应用场景	主要用于仿真场景	主要应用于实际无人驾驶场景
元素形式表达	使用曲线方程和基于参考线的偏移描述车道形状	使用绝对坐标序列描述元素形状
元素丰富度	提供常见的元素类型，如道路、交叉点、信号和对象	细化元素表达并丰富元素属性。如增加新的禁止停车区域、人行横道、减速带、停车线、允许停车标志、允许减速标志等。
自适应无人驾驶算法	N/A （不适用）	整合百度的无人驾驶经验，以提高无人驾驶算法的可行性和可靠性。

apollo地图包括道路定义、交叉路口、交通信号、车道规则以及汽车导航的其他元素

apollo高精度地图采用的openDRIVE格式，是一种行业制图标准，

高进度地图构建由五个过程组成：数据采集、数据处理、对象检测、手动验证和地图发布

 

人工智能检测静态对象并对其进行分类，其中包括车道线、交通标志、电线杆

定位

 定位的任务是确定你的车辆在这张高精度地图上的位置

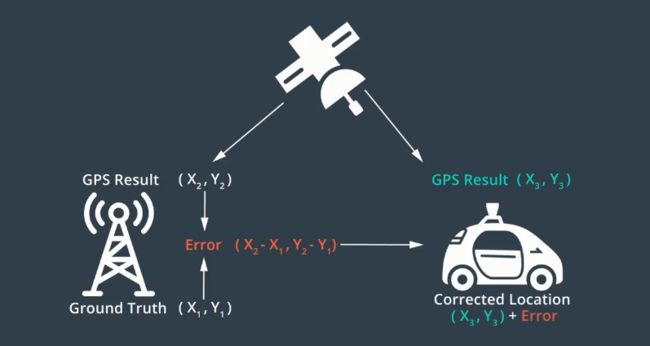
GPS定位在正常情况下，1-2m,山脉环绕地区10—15m

通过传感器确定车来那个与物体之间的距离

车辆传感器获取的地标与高精度地图中的地标进行对比

这张表总结了常见自动驾驶功能所使用的传感器，以及各个传感器的应用。

常见的无人驾驶定位方法如：GNSS RTK、惯性导航、LIDAR定位、视觉定位

GNSS RTK:三个卫星确定一个位置  通过地面基站计算误差，对GNSS予以补偿

 

惯性导航定位（IMU）通过陀螺仪实现，但是会出现误差累积的问题

lidar定位，最常见的方法是icp,优点在于它的稳健性，可以快速扫描与高精地图确定联系，缺点是需要实时更新地图

apollo使用的是直方图滤波算法（误差平方和算法SSD）。卡尔曼滤波是另一种lidar定位方法，卡尔曼滤波用于根据过去状态和新的测量结果预测当前结果

视觉定位：摄像机获取数据容易，但是定位很难，需要和别的传感器配合使用，常见定位方法：粒子滤波

 

apollo使用GPS、IMU 、和激光雷达的多传感器融合方法实现，这种方法利用了不同传感器的互补优势，提高了稳定性和准确性，apollo定位模块依赖IMU，GPS、雷达、激光雷达和高精度地图。同时支持GNSS定位和lidar定位。融合框架通过卡尔曼滤波将这些输出结合在一起，卡尔曼滤波建立在两部预测测量周期之上，惯性导航方案用于卡尔曼滤波的预测步骤，GNSS定位和LIDAR定位用于卡尔曼滤波的测量结果更新步骤。

感知

无人驾驶有四个感知世界的核心任务，检测，分类，跟踪，语义分割。

检测是指找出物体在环境中的位置

分类是指明确对象是什么

跟踪是指随时间推移观察移动物体

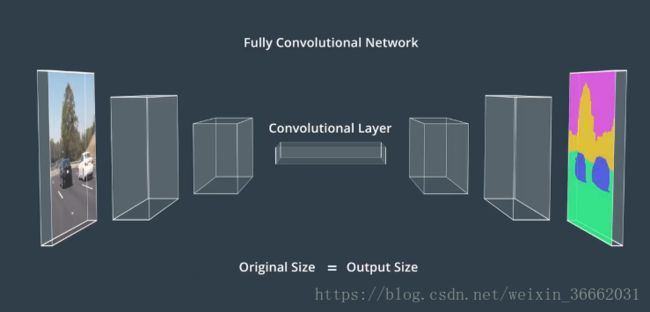
语义分割意味着将图像中的每个像素与语义类别进行匹配

图像分类器是一种将图像作为输入并输出标识该图像的标签的算法

基础知识

摄像头图像：rgb信息=长*宽*3

LIDAR图像：激光雷达通过激光束反射，他搜集的数据形成点云图，点云图可以告诉我们形状，表面纹理，通过对点进行聚类和分析，这些数据提供了足够的对象检测，跟踪和分类的信息

 

机器学习：包括监督学习，半监督学习，无监督学习，强化学习。强化学习允许模型尝试不同的方法来解决问题然后衡量哪种方法最为成功

人工神经网络：是通过数据来学习复杂模型的工具，通过调节这些识别出来的特征的权重来实现任务，首先随机分配权重，然后通过反向传播逆反馈调节，

检测、分类、跟踪、分割

检测和分类：通过CNN来查找图像中的对象位置，然后对其进行分类，经典的体系结构为R-CNN、Fast R-CNN、Faster R-CNN、YOLO、SSD。

跟踪：通过之前帧与当前帧的特征进行匹配，确定位置和速度，确定身份后结合预测算法，一股极下一时间速度与位置。跨帧跟踪目的是避免遮挡干扰

分割依赖于FCNN,保证输入与输出退休昂大小一致，需要先编码器编码，然后再用解码器解码

apollo实现过程     

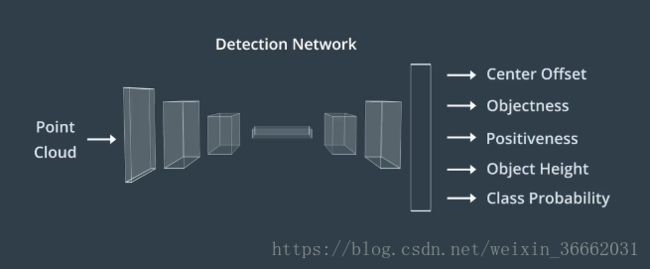
         apollo感知软件栈，对于三维对象检测，apollo在高精度地图上使用感兴趣区域ROI来重点关注相关对象，并将ROI滤波器应用于点云和图像数据以缩小搜索范围并加快感知，然后通过检测网络馈送已过滤的点云，输出用于构建围绕对象的三维边界框。最后，我们使用检测跟踪关联算法来跨时间步识别单个对象。该算法先保留每个时间步要跟着的对象列表，然后下一时间步找到每个对象最佳匹配。

        apollo利用高精地图确定前方是否有交通灯，通过摄像机确定是否有交通灯，以及交通灯的状态。如果前方有交通信号灯，则高精度地图会返回灯的位置。Apollo 使用检测网络对图像中的灯进行定位，然后 Apollo 从较大的图像中提取交通信号灯。Apollo 将裁剪的交通灯图像提供给分类网络以确定灯颜色，如果有许多灯，则系统需要选择哪些灯与其车道相关。Apollo 使用 YOLO 网络来检测车道线和动态物体 ，其中包括车辆、卡车、骑自行车的人和行人。在经过 YOLO 网络检测后，在线检测模块会并入来自其他传感器的数据，对车道线预测进行调整，车道线最终被并入名为“虚拟车道”的单一数据结构中。同样 也通过其他传感器的数据，对 YOLO 网络所检测到的动态对象进行调整，以获得每个对象的类型、位置、速度和前进方向。虚拟通道和动态对象均被传递到规划与控制模块

 

预测

    我们的无人车需要预测这些物体的行为，这样才能确保我们的无人车做出最佳决策，我们通过生成一条路径来预测一个物体行为，在环境中 我们会为所有其他的物体做出类似的预测，这些共同形成了在一段时间内的预测路径。在每一个时间段内 我们会为每一辆汽车重新计算预测他们新生成的路径，这些预测路径为我们无人车在规划阶段做出决策提供了必要信息。

    预测路径有实时性的要求，实时性是指我们想要算法的延迟越短越好，一辆车如果是 60 千米/每小时的速度，那么它在每 0.25 秒会行驶 5 米，所以我们需要确保我们的无人车在行驶之前，前方 5 米没有任何障碍物并且可以安全地穿行。下一个目标就是准确性，如果我们预测出相邻多车道的汽车，想并入我们的车道，我们需要减速。如果预测它会保持在自己的车道上行驶，我们需要我们做出的预测尽可能保持准确，这样才能帮助我们无人车做出很好的决策。预测模块也应该能够学习新的行为，当路上有很多车辆 情况将变得复杂，开发出每种场景的静态模型是不可能完成的任务，这就是为什么我们需要当我们遇到这样的问题时，预测模块能够学习新的行为，这可以使算法随着时间的推移而提升预测能力。

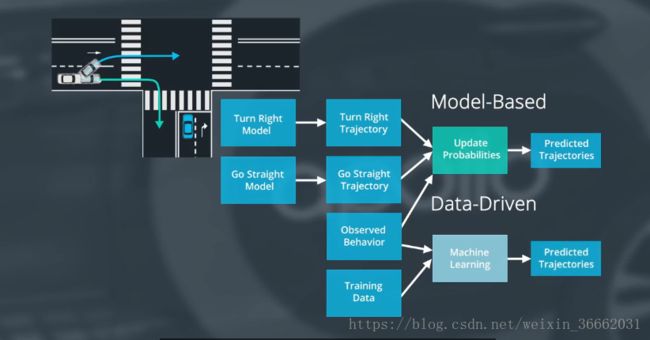
我们来介绍两种不同的预测方式，基于模型的预测与数据驱动预测，假设我们的无人车来到一个 T 型路口并且看到一辆车从左面行驶而来，此时 我们还不清楚，这辆车是要右转还是直行，用基于模型的方法，我们可以为此场景构建了两个候选的预测模型，一个模型描述了该车进行右转弯，另一个模型描述了该车继续直行。在此刻 我们认为任意一种模式发生的概率都是相同的，所以我们有两个候选模型 每个模型都有自己的轨迹。我们继续观察移动车的运动，看它与哪一条轨迹更加匹配。如果我们要看到车在右转弯车道保持前行，我们会更加倾向于预测对车辆右转，这就是基于模型预测方法的工作原理。数据驱动预测使用机器学习算法 通过观察结果来训练模型，一旦机器学习模型训练好，我们就可以在现实世界中利用此模型去做出预测。数据驱动方法的优点是 训练数据越多，模型效果越好，基于模型的方法的优点在于它的直观，并且它结合了我们现有的物理知识以及交通法规还有人类行为多方面知识

Apollo 提供了一种叫基于车道序列的方法，为了建立车道序列，我们首先将道路分成多个部分，每一部分都覆盖了一个易于描述车辆运动的区域，比如 这里是一个部分区域的十字路口，为了预测 我们更关心，车辆如何在这些区域内转换，而不是在某个区域内的具体行为，我们可以将车辆的行为划分为一组有限的模式组合，并将这些模式组合描述为车道序列，例如 直行汽车的运动可以描述为

     为了预测物体的运动，我们也需要知道物体的状态，当我们行驶时 作为人类，我们通过观察一个物体的朝向
位置、速度和加速度来预测它将会做什么，这同样是一辆无人驾驶汽车如何观察物体的状态，除了位置、速度 朝向和加速度之外，我们无人车还需考虑，车道段内物体的位置，例如 预测模块会考虑，从物体到车道线段边界的纵向和横向距离，预测模块还包含之前时间间隔的状态信息，以便做出更准确的预测。

     我们使用车道序列框架的目标是为道路上的物体生成轨迹，这是一个复杂的问题，我们先从一个稍微简单的问题开始，我们会预测车道线段之间的过渡，假设我们在车道段 0 中检测到一辆车，并且我们会预测在接下来的几个时间段中它将如何行驶，现在有两个显而易见的选择，它可能停留在车道段 0 然后向右转，或者可能转向车道段 1 然后直行，这个分析实际上是我们前进的一大步，我们已经将预测问题简化为选择问题，现在我们所要做的就是，选择车辆最有可能采取的车道顺序，我们可以通过计算每个车道序列的概率来进行选择，我们需要一个模型 将车辆状态和车道段作为输入 ，该模型用于提供车辆，可能采用每个车道序列的概率，我们希望我们的模型能够学习新的行为，因此应该使用观测数据对模型进行经验性训练，在训练中 ，我们将真实的车辆行为提供给模型 不仅包括车道段和对象的状态，还包括对象最终选择哪条车道序列，随着记录随着时间的增加，模型可以自我迭代更新 精确度不断提升，每个记录将由观察对象跟随的车道段序列，和对象的相关状态组成，在每个时间点，对象占用一段并具有特定的状态，整个记录由一系列车道段，和对象的相关状态组成

递归神经网络或 RNN 是一种利用时间序列数据特征的一种预测方法，在我们专门研究 RNN 之前，我们来回顾一下神经网络神经网络是可训练的多层模型，神经网络从输入，提取高级特征 并使用这些特征来计算得到输出，例如 如果你有一个神经网络，来分类图像是否包含汽车，网络的中间层将提取特征 如轮胎和窗户，神经网络有许多结构，一个基本的神经网络首先得到输入，然后将数据通过隐藏层，然后经过处理得到输出，这种结果有时也被称作多层感知网络 或 MLP，在训练的过程中 会有很多训练数据输入模型，每一个数据都由原始的数据和对应的标签组成，例如 输入数据是一张图片，而标签就是一个包含汽车的符号或者是其他符号，神经网络从数据中学习的方式叫做后向传播，首先 神经网络得到输入并产生输出，然后 计算机比较输出与真值之间的误差，接着 这种误差通过后向传回到整个网络，中间的隐藏层根据观察到的这种差别调整其中的中间值 或者叫权重，这样可以在未来提高神经网络的准确率，我们可以建立像这样的，多重结构的递归神经网络 我们称之为 MLP 单元，从数据序列中提取出高级特征，每个 MLP 单元将序列的一个元素作为输入，并预测序列的下一个元素作为输出，为了对元素之间的顺序关系建立模型，我们在每个单元之间建立一个额外的连接，这意味着每个单元根据原始输入，和前一个单元的输出进行预测，这是 RNN 的基本结构。

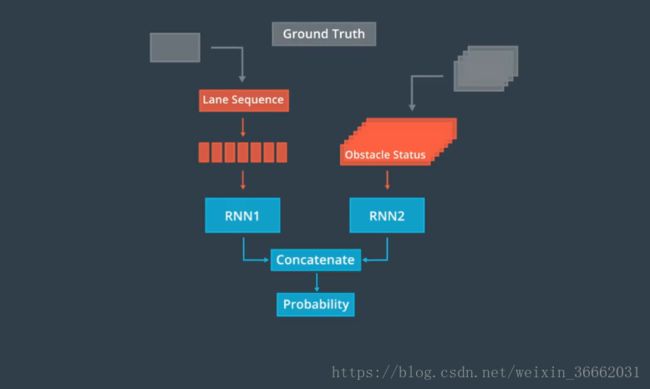
Apollo 使用 RNN 建立一个模型来预测车辆的目标车道，Apollo 为车道序列提供一个 RNN 模型，为相关对象状态提供另一个 RNN 模型，Apollo 连接这两个 RNN 的输出并将它们馈送到另一个神经网络，该神经网络会估计每个车道序列的概率，具有最高概率的车道序列是我们预测目标车辆将遵循的序列，为了训练这个网络，我们使用现有的记录，每条记录都包含一个车道序列，相关的对象状态和一个标签，用于指示对象是否遵循此特定车道序列，在训练中 我们比较网络输出和真值标记，并使用反向传播来训练网络

轨迹生成是预测的最后一步，一旦我们预测到物体的车道序列，我们就可以预测物体的轨迹，在任何两点 A 和 B 之间，物体的行进轨迹有无限的可能，我们如何预测最有可能的轨迹？，我们可以先通过设置约束条件，来去除大部分候选轨迹，首先 我们假定汽车将与目标车道的中心对齐，我们继续去除，车辆无法实际执行的轨迹，我们通过考虑车辆当前的速度和加速度从剩余的轨迹中进行选择，实际上 我们并没有实际列出，所有可能的轨迹并逐一去除它们，相反 我们只是在数学理论上来应用这一想法，注意车辆在两点的位置和方位，这两个姿势表示运动模型的初始状态和最终状态，我们可以使用这两个条件来拟合一个多项式模型，在大多数情况下 这种多项式足以进行预测

你已经学会了无人车如何预测道路上物体的行为，以及如何使用轨迹来描述它们的行为，让我们回顾这一课的主要内容，我们首先介绍了如何将复杂的车辆运动，转换为车道转换序列，这使我们能够大大减少场景的数量，并更快地进行预测，然后 我们介绍了如何使用现有观测值，以车道序列表示，训练神经网络来进行预测，最后 我们将车道序列预测与车辆物理结合起来，为每个物体生成估计的轨迹，运动预测对于在规划中构建无碰撞的安全路径来说 至关重要

规划

      在规划中 我们通过结合高精度地图，定位和预测来构建车辆轨迹，规划的第一步是路线导航，侧重于如何从地图上的 A 前往 B，在进行路线规划时 将地图数据作为输入 并输出可行驶路径，手机导航系统是路线规划的一个示例，在 Apollo 中 通过路线规划模块处理该任务，一旦我们构建了高水平的路线，我们就会放大至轨迹规划，通过轨迹规划 我们可以做出微妙的决策，以避开障碍物 并为乘客创造平稳的乘车体验，在 Apollo 中 我们通过规划模块处理该任务，轨迹规划的目标是生成免碰撞和舒适的可执行轨迹，该轨迹由一系列点定义，每个点都有一个关联速度，和一个指示何时应抵达那个点的时间戳

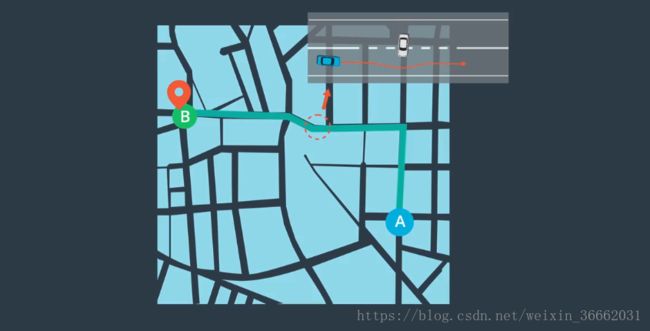
路线规划的目标是 找到从地图上的 A 前往 B 的最佳路径，路线规划使用了三个输入，第一个输入为地图，Apollo 提供的地图数据包括公路网和实时交通信息。第二个输入为我们当前在地图上的位置，第三个输入为我们的目的地，目的地通常取决于车辆中的乘客，有了这三个输入，路线规划模块就为寻找前往目的地的路径做好了准备

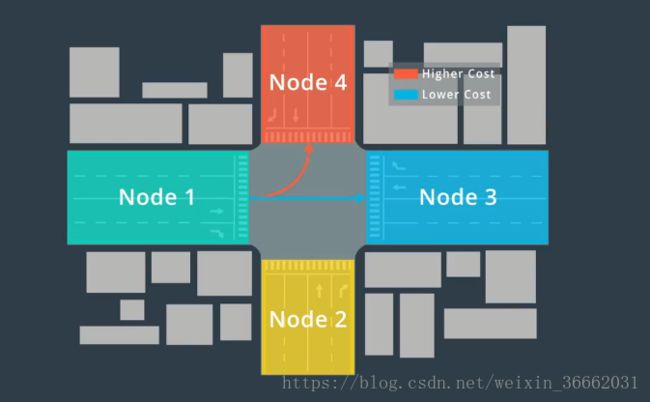
    当人们试图在地图上找到从 A 到 B 的路线时，通常会沿着道路追踪路径 以查看是否存在通往目的地的任何路径，这被称为搜索，Apollo 也通过搜索来查找路线，但它使用了更智能的搜索算法，在 Apollo 开始搜索之前，它将地图数据重新格式化为“图形”的数据结构，该图形由“节点”和“边缘”组成，节点代表路段，边缘代表这些路段之间的连接，例如 在交叉路口，汽车可从节点 1 移动到节点 2，节点 3 或节点 4 反之亦然，我们也可以对从一个节点移动到另一个节点所需的成本进行建模，例如 在现实生活中，拐过一个交叉路口比直行更费劲，所以从节点 1 到节点 4 的成本，高于从节点 1 到节点 3 的成本，将地图转换为图形的好处在于，在计算机科学领域中 人们已发现许多用于在图形中查找路径的快速算法，一旦我们在图形中找到了一条好路径，就可以轻松地将图形中的路径重新转换为地图上的路径

A *是经典的路径查找处理算法，演示一下 A* 如何通过网格工作，我们将该网格中的每个单元格当做一个节点，我们能够从任何一个节点移动到其任意相邻节点，这个特殊网格包含一些阻挡潜在路径的墙壁。对人类来说，通过查看图形便可以轻易找出最佳路径，但对于计算机而言 这并不明显，计算机必须检查是否存在通往目的地的任何路径，计算机可能竭尽所能地尝试所有可能的路径 以找到最短的路径，但是 这需要耗费大量时间，尤其是在地图非常大的时候，从任何给定的节点来看，我们最多有 8 个用于下一步的选项，因为存在 8 个相邻的单元格，对于这 8 个选项中的每一个，我们在下一步有另外 8 个选项，如果我们展开所有节点，搜索量将暴增至即使最快的计算机 也无法处理的程度。从初始节点开始，我们需要确定 8 个相邻节点中，哪个是最有希望的候选节点，对于每个候选节点，我们考虑两件事情，首先，我们计算从开始节点到候选节点的成本，然后，我们估计从候选节点前往目的地的成本，计算前往候选节点的成本很容易，因为它已经与我们相邻，计算从候选节点到目的地的成本很困难，但是 通过简单计算，从候选节点到目的地的距离 我们通常可以做出很好的估计，我们使用变量 g 和 h 来表示每个成本，g 值为从开始节点前往候选节点的成本，h 值为从候选节点，前往目的地的估计成本或启发式成本，根据我们的具体情况，我们可以自定义成本估算方式，例如 交通堵塞会增加前往目的地的成本，所以交通繁忙的路径具有更高的成本，对于每个候选节点，我们通过添加 g 值和 h 值来计算总和，即 f 值，最佳候选节点是 f 值最小的节点，每当我们抵达新节点时，我们通过重复此过程来选择下一个候选节点，而且总是选择我们尚未访问过，且具有最小 f 值的节点，这就是 A * 算法，它建立了一条稳定前往目的地的路径

现在我们来考虑一下真实世界中的地图，假设我们到达了一个交叉路口，我们可以沿着公路直走，右转或左转，首先 我们将把这张地图转换为具有三个候选节点的图形，接下来 我们将对选项进行评估，在实践中 拐过交叉路口很费劲，所以我们为这个节点分配了更高的 g 值，g 值是从起始点到候选节点的成本，在查看公路选项之后，我们意识到必须走很长的路，才能离开公路 并返回我们的目标，所以我们为该选项分配了更高的 h 值，h 值是从候选节点到目的地的估计成本，接下来 我们通过将 g 值和 h 值相加来计算每个节点的 f 值，我们看到 最低 f 值实际对应右边的候选节点，所以 这是我们接下来要前往的节点

高等级地图路线只是规划过程的一部分，我们仍需要构建沿这条路线前进的低等级轨迹，这意味着要处理不属于地图的物体，如其他车辆、自行车或行人，例如 我们可能需要与，试图在我们前面掉头的汽车互动，或者我们可能希望在公路上驶过一辆慢车，这些场景需要更低级别 更高精确度的规划，我们将这一级别的规划称为 轨迹生成

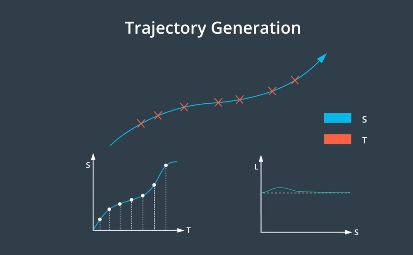
轨迹生成的目标是生成由一系列路径点所定义的轨迹，我们为每个路径点分配了一个时间戳和速度，我们让一条曲线与这些路径点拟合，生成轨迹的几何表征，由于移动的障碍物可能会暂时阻挡部分路段，轨迹中的每个路点都有时间戳，我们可以将时间戳与预测模块的输出相结合，以确保在我们计划通过时，轨迹上的每个路径点均未被占用，这些时间戳创建了一个三维轨迹，每个路径点由空间中的两个维度，以及时间上的第三个维度来定义，我们还为每个路径点指定了一个速度，速度用于确保车辆按时到达每个路径点

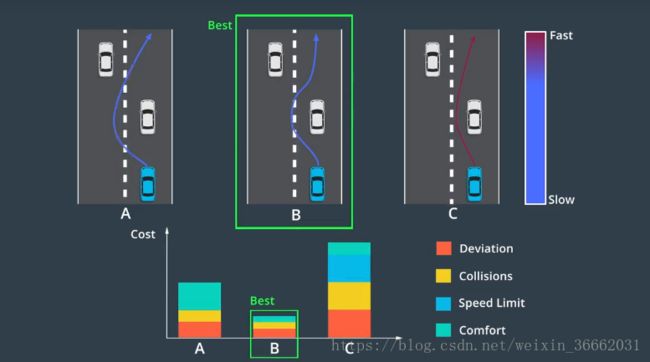
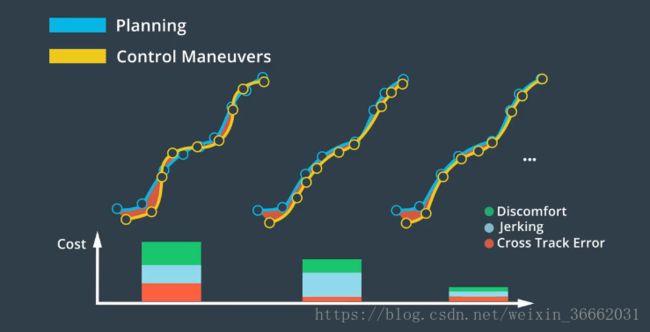
现实世界中的规划面临多种约束，首先 轨迹应能免于碰撞，这意味着必须无障碍物，其次 要让乘客感到舒适，所以 路径点之间的过渡以及速度的任何变化都必须平滑，再者 路径点对车辆应实际可行，例如 高速行驶的汽车不能立即做 180 度转弯，我们不能构建包含这种不可行机动的轨迹，最后 轨迹应合法，我们需要了解每个路径点的交通法律，并确保轨迹遵守这些法律法规。可能会有多个不会碰撞，舒适、可行且合法的轨迹，我们如何选择最佳轨迹呢？答案是使用“成本函数”，成本函数为每个轨迹分配了一个“成本”，我们选择成本最低的轨迹，轨迹“成本”由各种犯规处罚组成，例如 偏离道路中心，有可能会碰撞，超出速度限制，或轨迹的曲率和加速度让乘客感到不舒服均会使成本增加，轨迹成本将所有这些缺陷聚合为单个数字，这使我们能对不同的轨迹进行排名，车辆甚至可能在不同的环境中使用不同的成本函数，例如 高速公路的成本函数，可能与停车场的成本函数不同

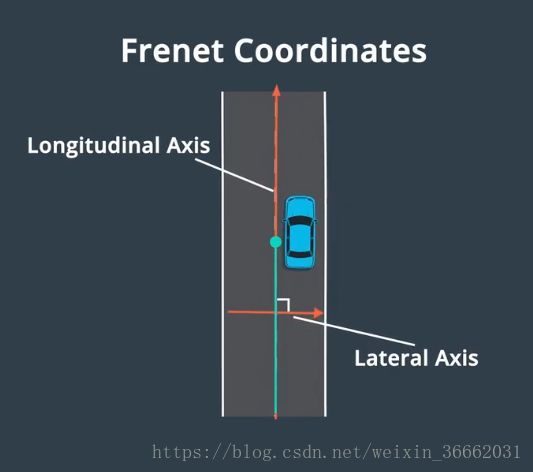
我们通常使用笛卡尔坐标系描述物体的位置，但笛卡尔坐标系对车辆来说并不是最佳选择，即使给出了车辆位置 (x, y)，如果我们不知道道路在哪里，也很难知道车辆行驶了多远，也难以确定它是否偏离车道中心，笛卡尔坐标系的替代解决方案为 Frenet 坐标系，Frenet 坐标系描述了汽车相对于道路的位置，在 Frenet 框架中，s 代表沿道路的距离，也被称为纵坐标，d 表示与纵向线的位移，也被称为横坐标，在道路的每个点上，横轴和纵轴都是垂直的，纵坐标表示在道路中的行驶距离，横坐标表示汽车偏离中心线的距离

路径-速度解耦规划将轨迹规划分为两步：路径规划和速度规划，首先 在路径规划步骤中，生成候选曲线，这是车辆可行驶的路径，我们使用成本函数对每条路径进行评估，该函数包含平滑度、安全性、与车道中心的偏离，以及我们想要考虑的其他任何因素，我们按成本对路径进行排名，并选择成本最低的路径，下一步是确定沿这条路线行进的速度，我们可能希望改变在该路径上的速度，所以我们真正需要选择的是与路径点相关的一系列速度，而不是单个速度，我们将该序列称作“速度曲线”，我们可以使用优化功能为路径选择，受到各种限制的良好速度曲线，通过将路径和速度曲线相结合 可构建车辆行驶轨迹

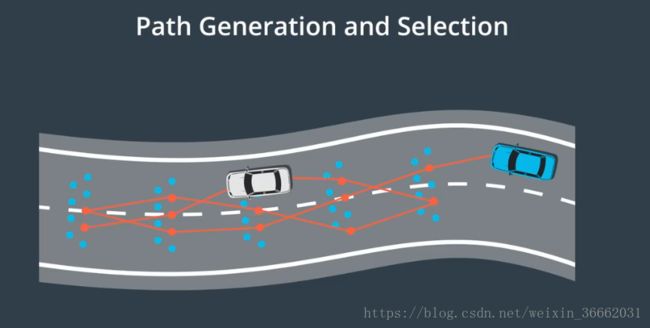
为了在路径-速度解耦规划中生成候选路径，我们首先将路段分割成单元格，然后对这些单元格中的点进行随机采样，通过从每个单元格中取一个点并将点连接，我们创建了候选路径，通过重复此过程 我们可以构建多个候选路径，我们使用成本函数对这些路径进行评估，并选择成本最低的路径，成本函数可能考虑以下因素，与车道中心的偏离，与障碍物的距离，速度和曲率的变化，对车辆的压力，或我们希望列入的任何其他因素

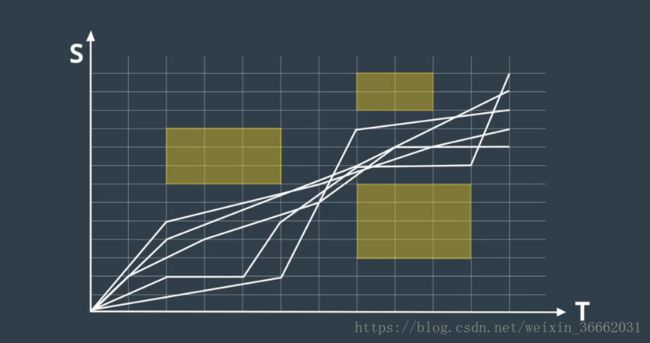
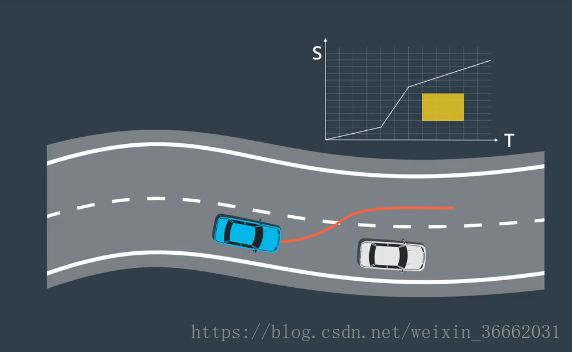
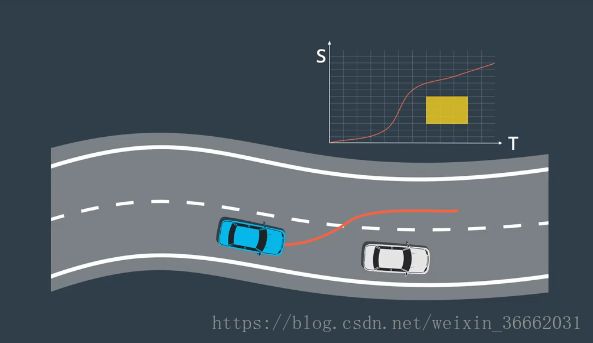
选择路径后的下一步，是选择与该路径关联的速度曲线，一个被称为“ST 图”的工具可以帮助我们设计和选择速度曲线，在 ST 图中，“s”表示车辆的纵向位移 “t”表示时间，ST 图上的曲线是对车辆运动的描述，因为它说明了车辆在不同时间的位置，由于速度是位置变化的速率，所以我们可以通过查看曲线的斜率从 ST 图上推断速度，斜坡越陡 则表示，在更短的时间段内有更大的移动 对应更快的速度

为构建最佳速度曲线，我们需要将 ST 图离散为多个单元格，单元格之间的速度有所变化，但在每个单元格内 速度保持不变，该方法可简化速度曲线的构建，并维持曲线的近似度，在 ST 图中，可以将障碍物绘制为在特定时间段内，阻挡道路的某些部分的矩形，例如 假设预测模块预测车辆，将在 t0 到 t1 的时间段内驶入我们的车道，由于该车将在此期间占据位置 s0 到 s1，因此我们在 ST 图上绘制了一个矩形，它将在时间段 t0 到 t1 期间阻挡位置 s0 到 s1，为避免碰撞，速度曲线不得与此矩形相交，既然有了一张各种单元格被阻挡的 ST 图，我们便可以使用优化引擎为该图选择最佳的速度曲线，优化算法通过复杂的数学运算来搜索，受到各种限制的低成本解决方案，这些限制可能包括：法律限制 如速度限制 ，距离限制 如与障碍物的距离，汽车的物理限制 如加速度限制

路径-速度解耦规划在很大程度上取决于离散化，路径选择涉及将道路划分为单元格，速度曲线构建涉及将 ST 图划分为单元格，尽管离散化使这些问题更容易解决，但该解决方案生成的轨迹并不平滑，为了将离散解决方案转换为平滑轨迹，我们可使用“二次规划”技术，二次规划将平滑的非线性曲线与这些分段式线性段拟合，尽管二次规划背后的数学运算很复杂，但对我们的目的而言，细节并不是必需的，我们只需简单使用几种不同的优化包中的一种，包括一种由 Apollo 推出的运行方案 来生成平滑的轨迹，一旦路径和速度曲线就绪，我们便可以用其构建三维轨迹

我们来回顾一下端到端路径-速度解耦规划，假设我们正在路上行驶，感知系统观察到 一辆缓慢行驶的车辆离我们越来越近，首先 我们在这辆车的周围生成多条候选路线，我们使用成本函数对这些候选路径进行评估，并选择成本最低的路径，然后我们使用 ST 图来进行速度规划，我们根据其他车辆随时间变化的位置阻挡了 ST 图的部分区域，优化引擎可帮助我们确定该图的最佳速度曲线 该曲线受制于约束和成本函数，我们可以使用二次规划让路径和速度曲线变平滑，最后 我们将路径和速度曲线合并构建轨迹，这里的轨迹在速度较快时为红色，在速度较慢时为蓝色，我们使用该轨迹来安全地绕开其他车辆 并继续我们的旅程

 Lattice 规划的轨迹生成方法，通过使用 Frenet 坐标 我们可以将环境投射到，纵轴和横轴上，我们的目标是生成三维轨迹 - 纵向维度，横向维度和时间维度，我们可以将三维问题分解成，两个单独的二维问题，这是通过分离轨迹的纵向和横向分量来解决的，其中一个二维轨迹是具有时间戳的纵向轨迹，我们称之为 ST 轨迹，另一个二维轨迹是，相对于纵向轨迹的横向偏移，我们称之为 SL 轨迹，Lattice 规划具有两个步骤，即先分别建立 ST 和 SL 轨迹 然后将它们合并，为生成纵向和横向二维轨迹，我们先将初始车辆状态投射，到 ST 坐标系和 SL 坐标系中，通过对预选模式中的多个候选最终状态进行采样，我们来选择最终车辆状态，对于每个候选最终状态，我们构建了一组轨迹，将我们的车辆从其初始状态转换为最终状态，我们使用成本函数对这些轨迹进行评估，并选择成本最低的轨迹

根据情况 我们可以将状态分成 3 组，巡航 、跟随与停止，巡航 意味着车辆将在完成规划步骤后定速行驶，我们实际上在对图上的点进行采样，在图中 横轴代表时间 纵轴代表速度，对于该图上的点，这意味着汽车将进入巡航状态，在时间 t 以 s 点的速度巡航 对于这种模式，所有最终状态的加速度均为零，下一个要考虑的模式为跟随车辆，在这种情况下 我们要对位置和时间状态进行采样，并尝试在时间 t 出现在某辆车后面 在跟随车辆时，我们需要与前方的车保持安全距离，这时 速度和加速度将取决于我们要跟随的车辆，这意味着 在这种模式下，速度和加速度都会进行修正，最后一种模式是停止，对于这种模式 我们只需对汽车何时何地停止进行抽样，这里 速度和加速度会被修正为 0

我们会根据这样一个假设来进行 SL 规划，即无论车辆进入怎样的终止状态，车辆都应该稳定地与车道中心线对齐，这意味着我们只需要在一个小区域内 对横向终止位置进行采样，具体来说，我们采样的是道路上相邻车道中心线周围的位置，为了确保稳定性，汽车驶向的终止状态应该与车道中心一致，当我们用横向位置与纵向位置作图时 ，我们想要的候选轨迹应该，以车辆与车道对齐并直线行驶而结束，为了达到这种终止状态，车的朝向和位置的一阶和二阶导数，都应该为零，这意味着车辆既不是横向移动的那是一阶导数，也不是横向加速 那是二阶导数，这意味着车辆正沿着车道直行

一旦我们同时拥有了 ST 和 SL 轨迹，我们就需要将它们重新转换为笛卡尔坐标系，然后 可以将它们相结合，构建由二维路径点和一维时间戳组成的三维轨迹，ST 轨迹是随时间变化的纵向位移，SL 轨迹是，纵向轨迹上每个点的横向偏移，由于两个轨迹都有纵坐标 S，所以我们可以通过将其 S 值进行匹配来合并轨迹

我们探讨了无人驾驶车如何规划行驶的轨迹，车辆基于高精度地图、感知和预测模块的数据来进行这一规划，首先 我们介绍了如何使用 A * 算法 规划前往目的地的地图级路线，然后 我们专注于构建，逐步引导我们前往目的地的免碰撞轨迹，我们学习了如何构建这些轨迹，借助路径—速度解耦规划或 Lattice 规划，通过比较这两种方法 你会有更为直观的认知，更好地理解规划 以及如何使用成本函数选择轨迹，规划是无人驾驶车开发过程中最困难的部分之一，你应该为熟悉解决该问题的，几个不同的方法感到非常自豪

控制

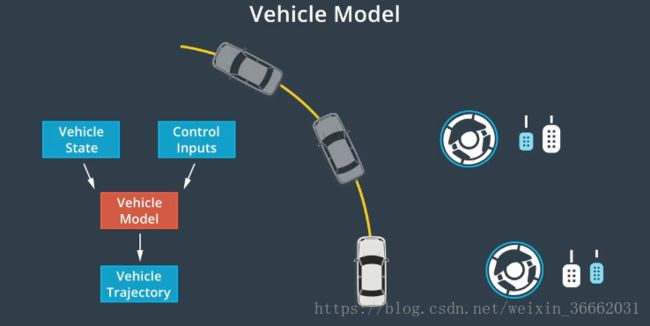
在该模块中 你将学习如何使用控制来运行轨迹，控制是驱使车辆前行的策略，对于汽车而言 最基本的控制输入为转向、加速和制动，通常 控制器使用一系列路径点来接收轨迹，控制器的任务是使用控制输入，让车辆通过这些路径点，首先 控制器必须准确，这意味着它应避免偏离目标轨迹，这对于安全性来说 这尤为重要，即使路面潮湿或道路比较陡峭，控制器仍需要精确地执行轨迹，其次 控制策略对汽车应该具备可行性，例如 如果你的汽车向北行驶 而你希望它立即向东转，你可以在游戏中做到这一点，但在现实生活中无法实现，最后 需要考虑的一点是平稳度，舒适的驾驶非常重要，如果车辆行驶得不规律，那乘客永远不会想再次乘坐它了，要使控制顺利进行，驱动必须是连续的，这意味着你应避免突然转向，加速或制动，总之 我们的目标是使用可行的控制输入，最大限度地降低与目标轨迹的偏差，最大限度地提高乘客的舒适度，让我们来回顾一下 可用于实现这些目标的三种控制策略，比例积分微分控制(或 PID)，线性二次调节器(或 LQR)，以及模型预测控制(或 MPC)，最后 我们希望你能够领会几种不同的车辆控制策略

控制器的输出是，控制输入（转向、加速和制动）的值，当偏离目标轨迹时，我们希望通过采取行动来纠正这种偏差，对于普通汽车，我们使用方向盘控制行驶方向（即转向），使用油门加速，使用刹车减速（即制动），这也正是无人驾驶汽车所做的，一旦将这三个值传递给车辆，汽车实际上已经开始无人驾驶了！
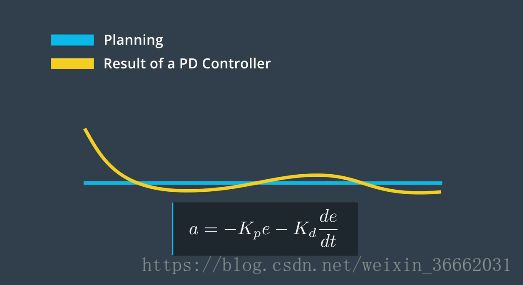
     第一个算法称为 PID 控制，这个控制器的优点在于它非常简单，只需知道与目标轨迹有多大的偏离，PID 的第一个组件为 P 代表“比例”(proportional)，设想一辆车正试图遵循目标轨迹，P 控制器在车辆开始偏离时，立即将其拉回目标轨迹，比例控制意味着 车辆偏离越远，控制器就越难将其拉回目标轨迹

在实践中 P 控制器的一个问题在于，它很容易超出参考轨迹，当车辆越来越接近目标轨迹时 ，我们需要控制器更加稳定，PID 控制器中的 D 项致力于 使运动处于稳定状态，D 代表“微分”（derivative），PD 控制器类似于 P 控制器，它增加了一个阻尼项，可最大限度地减少控制器输出的变化速度

PID 控制器中的最后一项 I 表示积分(Integral)，该项负责纠正车辆的任何系统性偏差，例如 转向可能失准，这可能造成恒定的转向偏移，在这种情况下 我们需要稍微向一侧转向，以保持直行，为解决这一问题 控制器会对系统的累积误差进行惩罚，我们可以将 P、I 和 D 组件结合，构成 PID 控制器

PID 控制器很简单，但它在很多情况下的效果很好，对于 PID 控制器，你只需知道你的车辆与目标轨迹之间的偏差，但是 PID 控制器只是一种线性算法，对于非常复杂的系统而言 这是不够的，例如 为控制具有多个关节的四轴飞行器或机器人，我们需要建立机器人的物理模型，对无人驾驶车而言，我们需要应用不同的 PID 控制器来控制转向和加速，这意味着很难将横向和纵向控制结合起来，另一个问题在于 PID 控制器依赖于实时误差测量，这意味着受到测量延迟限制时可能会失效

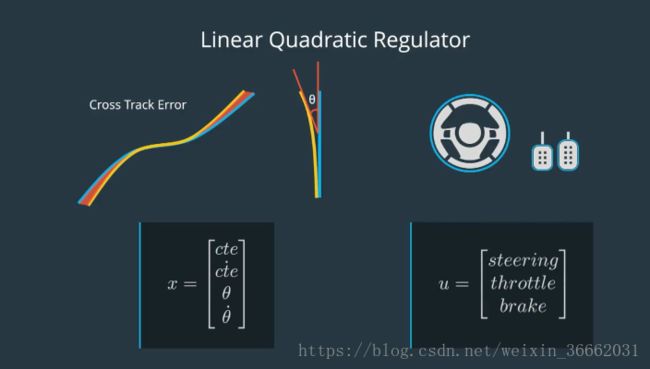
线性二次调节器（或 LQR），是基于模型的控制器，它使用车辆的状态来使误差最小化，Apollo 使用 LQR 进行横向控制，横向控制包含四个组件：横向误差，横向误差的变化率，朝向误差，和朝向的变化率，变化率与导数相同，我们用变量名上面的一个点来表示这个，我们称这四个组件的集合为 x，这个集合 x 捕获车辆的状态，除了状态之外，该车有三个控制输入：转向、加速和制动，我们将这个控制输入集合称为 u，LQR 处理线性控制，这种类型的模型可以用等式来表示，

X(上方带点) = Ax + Bu，X(上方带点)向量是导数，或 x 向量的变化率，所以 x 点的每个分量只是 x 相应分量的导数。等式 x 点 = Ax + Bu，该等式捕捉 状态里的变化，即 x 点  是如何受当前状态 x ，和控制输入 u 的影响的，

这个等式是线性的，因为当我们用 △x 来改变 x 时，并用 △u 来改变 u ，x 点的变化 也会让这个等式成立，现在我们理解了 LQR 中的 L，那么 Q 呢？这里的目标 就像控制的目标一样典型，是为了让误差最小化，但我们也希望尽可能少地使用控制输入，由于使用这些会有成本，例如 耗费气体或电力，为了尽量减少这些因素，我们可以保持误差的运行总和，和控制输入的运行总和，当汽车往右偏转得特别厉害之际，添加到误差总和中，当控制输入将汽车往左侧转时，从控制输入总和中减去一点，然而 这种方法会导致问题，因为右侧的正误差，只需将左侧的负误差消除即可，对控制输入​​来说也是如此，相反 我们可以让 x 乘以 u，这样 负值也会产生正平方，我们称这些为二次项，我们为这些项分配权重 并将它们加在一起，最优的 u 应该加倍减总和，在数学中 我们将这个值称为成本函数，

我们经常写出加权二次项的总和，以紧凑的矩阵形式呈现，这里 Q 和 R 代表 x 和 u 的权重集合，Xt 和 Ut 是转置矩阵，这意味着它们几乎与 x 和 u 相同，只是重新排列 以便矩阵乘法，x 乘以 Xt u 乘以 Ut，实质上是将每个矩阵乘以它自己，最小化成本函数是一个复杂的过程，但通常 我们可以依靠数值计算器为我们找到解决方案，Apollo 就提供了一个这样的求解方案，在 LQR 中，控制方法被描述为 u = -Kx，其中 K 代表一个复杂的 skeme，代表如何从 x 计算出 u，所以找到一个最优的 u 就是找到一个最优的 K，许多工具都可以轻松地用来解决 K，尤其当你提供了模拟车辆物理的 A、B，以及 Q、R 它们是 x 和 u 的权重

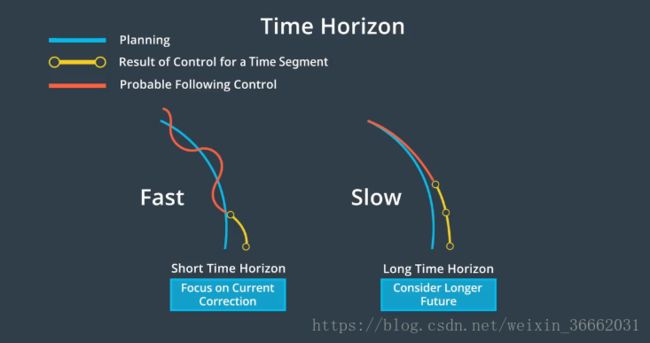
模型预测控制（或 MPC），是一种更复杂的控制器 它非常依赖于数学优化，但基本上可以将 MPC 归结为三个步骤，1.建立车辆模型，2.使用优化引擎计算有限时间范围内的控制输入，3.然后执行第一组控制输入，MPC 是一个重复过程，它着眼未来，计算一系列控制输入，并优化该序列，但是控制器实际上只实现了，序列中的第一组控制输入，然后控制器再次重复该循环，为什么我们不执行整个控制输入序列呢？，那是因为我们仅只采用了近似测量与计算，如果实现了整个控制输入序列，实际产生的车辆状态将与我们的模型有很大差异，最好在每个时间步不断地重新评估，控制输入的最优序列

MPC 的第一步为定义车辆模型，该模型近似于汽车的物理特性，特别是 该模型估计了，假如将一组控制输入应用于车辆时会发生什么，接下来 我们决定 MPC 预测未来的能力，预测越深入，控制器就越精确，不过需要的时间也越长，所以 我们需要在准确度与快速获取结果之间做出取舍，获取结果的速度越快，越能快速地将控制输入应用到实际车辆中，下一步是将模型发送到，搜索最佳控制输入的优化引擎，该优化引擎的工作原理，是通过搜索密集数学空间来寻求最佳解决方案，为缩小搜索范围，优化引擎依赖于车辆模型的约束条件

优化引擎可间接评估控制输入，是通过使用这些方法对车辆轨迹进行建模的，可根据成本函数对轨迹进行评估，成本函数主要基于与目标轨迹的偏差，其次 基于其他因素 如加速度，和提升乘客舒适度的措施，为使乘客感觉更舒适，对控制输入的调整应该很小，因为动作变化幅度过大会让乘客感到不舒服，根据具体情况，我们可能需要为其考虑进一步的成本，并设计成本函数，模型、约束和成本函数合并在一起，并作为优化问题加以解决，我们可以在不同的优化引擎中 选择一种来寻找最佳解决方案

Apollo 支持所有这三种控制器

模型预测控制考虑了车辆模型，因此比 PID 控制更精确，它也适用于不同的成本函数，所以我们可以在不同情况下优化不同的成本，另一方面 与 PID 控制相比，模型预测控制相对更复杂、更缓慢、更难以实现，在实践中 无人驾驶车的控制可扩展性的重要程度，通常意味着值得为 MPC 投入实现成本，所以 MPC 成为了一个非常重要的无人驾驶车控制器